Gauss-Seidel Method Förklaring, applikationer, exempel

han Gauss-Seidel Method Det är en iterativ procedur att hitta ungefärliga lösningar på ett system med linjära algebraiska ekvationer med godtyckligt vald precision. Metoden gäller för fyrkantiga matriser med icke -nollelement i dess diagonaler och konvergens garanteras om matrisen är diagonalt dominerande.

Det skapades av Carl Friedrich Gauss (1777-1855), som gjorde en privat demonstration till en av hans studenter 1823. Därefter publicerades det formellt av Philipp Ludwig Von Seidel (1821-1896) 1874, därmed namnet på båda matematiker.

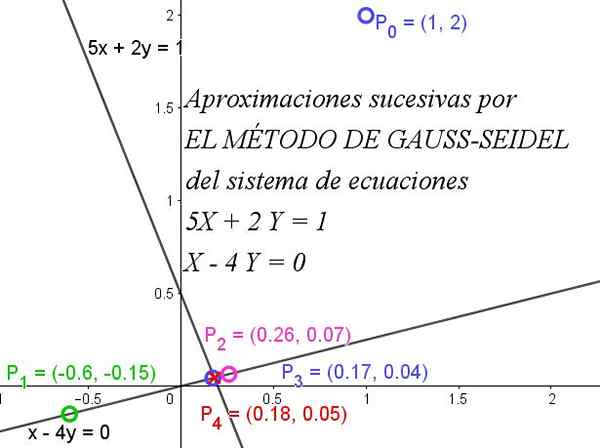
Figur 1. Gauss-Seidels metod konvergerar snabbt till att få ett system med ekvationer. Källa: f. Zapata.

För en fullständig förståelse av metoden är det nödvändigt att veta att en matris är diagonalt dominerande när det absoluta värdet för det diagonala elementet i varje rad är större än eller lika med summan av de andra elementens absoluta värden samma rad.

Matematiskt uttrycks det enligt följande:

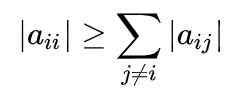
[TOC]

Förklaring genom ett enkelt fall

För att illustrera vad Gauss-Seidel-metoden kommer att ta ett enkelt fall där du kan hitta värdena på X och Y i det 2 × 2 linjära ekvationssystemet som visas nedan:

5x + 2y = 1

X - 4y = 0

Steg att följa

1- Först och främst måste du avgöra om konvergensen är säker. Det observeras omedelbart att det i själva verket är ett diagonalt dominerande system, eftersom den första koefficienten i den första raden har ett större absolut värde än de andra i den främre raden:

| 5 |> | 2 |

På samma sätt är den andra koefficienten för den andra raden också diagonalt dominerande:

| -4 |> | 1 |

2- Variablerna x och y är tydliga: 

X = (1 - 2y)/5

Y = x/4

3- Ett initialt godtyckligt värde placeras, kallat "frö": xo = 1, me = 2.

4

Det kan tjäna dig: uppskattning med intervall

X1 = (1 - 2 me)/5 = (1 - 2 × 2)/5 = -3/5 

Y1 = x1 / 4 = (-3/5) / 4 = -3/20 

5- Fortsätt på liknande sätt för att erhålla den andra tillnärmningen av lösningen av ekvationssystemet:

X2 = (1 - 2 y1)/5 = (1 - 2x (-3/20))/5 = 13/50 

Y2 = x2/4 = (13/50)/4 = 13/200

6- Tredje iteration:

X3 = (1 - 2 y2)/5 = (1 - 2 (13/200))/5 = 87/500

Y3 = x3/4 = (87/500)/4 = 87/2000

7- Fjärde iteration, som den slutliga iterationen av detta illustrativa fall:

X4 = (1 - 2 y3)/5 = (1 - 2 (87/2000))/5 = 913/5000

Y4 = x4/4 = (913/5000)/4 = 913/20000

Dessa värden sammanfaller ganska bra med lösningen som hittades genom andra upplösningsmetoder. Läsaren kan kontrollera det snabbt med hjälp av ett matematiskt program online.

Metodanalys

Som man kan se, i Gauss-seidel-metoden, måste de ungefärliga värdena som erhållits för den tidigare variabeln i samma steg bytas ut i följande variabel. Detta skiljer det från andra iterativa metoder som Jacobi, där varje steg kräver tillvägagångssätt till föregående steg. 

Gauss-Seidels metod är inte en parallell procedur, medan Gauss-Jordan är. Det är också anledningen till att Gauss-Seidel-metoden har en snabbare konvergensfri steg än Jordans metod.

När det gäller det diagonalt dominerande matristillståndet är detta inte alltid nöjd. Men i de flesta fall räcker det för att byta ut det ursprungliga systemets rang för att uppfylla tillståndet. Dessutom konvergerar metoden nästan alltid, även när det diagonala dominansvillkoret inte uppfylls.

Det föregående resultatet, erhållet med fyra iterationer av Gauss-Seidel-metoden, kan skrivas på ett decimal sätt:

Kan tjäna dig: hur många symmetrixlar har en cirkel?

X4 = 0,1826

Y4 = 0,04565

Den exakta lösningen på systemet med uppförda ekvationer är:

X = 2/11 = 0,1818

Y = 1/22 = 0,04545.

Så bara med fyra iterationer erhålls ett resultat med en tusendel av precision (0,001).

Figur 1 illustrerar hur successiva iterationer snabbt konvergerar till den exakta lösningen.

Ansökningar

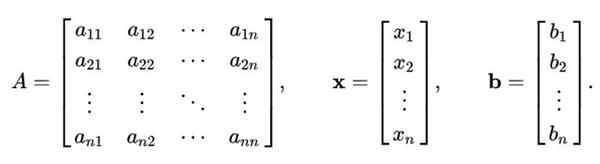
GAUSS-SEIDEL-metoden är inte bara begränsad till 2 × 2 linjära ekvationer. Ovanstående procedur kan generaliseras för att lösa ett linjärt system av n ekvationer med n Okända, som representeras matriser så här:

TILL X = b

Var TILL Det är en matris n x n, medan X Det är vektor -n -komponenterna i variablerna som ska beräknas; och b Det är en vektor som innehåller värdena på oberoende termer.

För att generalisera sekvensen för iterationer som tillämpas i det illustrativa fallet på ett N X N -system, som vill beräkna variabeln Xi, Följande formel kommer att gälla:

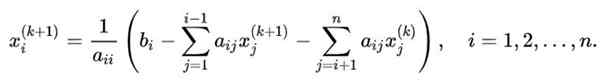
I denna ekvation:

- k Det är indexet för det värde som erhålls i iterationen k.

-K+1 Anger det nya värdet i följande.

Det sista antalet iterationer bestäms när värdet erhålls i iterationen K+1 skiljer sig från det erhållna omedelbart före, i ett belopp ε som är just den önskade precisionen.

Exempel på Gauss-Seidel-metoden

- Exempel 1

Skriv en allmän algoritm som låter dig beräkna den ungefärliga lösningsvektorn X av ett linjärt system med NXN -ekvationer, med tanke på koefficientmatrisen TILL, Vektorn med oberoende termer b, Antalet iterationer (iter) och vektorns initiala eller "frö" X.

Lösning

Algoritmen består av två "för" cykler, en för antalet iterationer och den andra för antalet variabler. Det skulle vara följande:

För K ∊ [1 ... iter]

För i ∊ [1 ... n]

X [i]: = (1/a [i, i])*(b [i] - ∑_{J = 1}ⁿ(A [i, j]*x [j]) + a [i, i]*x [i])

Kan tjäna dig: decimal notation

- Exempel 2

Kontrollera driften av den tidigare algoritmen genom att ansöka till matematisk programvara SMATH -studio Gratis och gratis, tillgängligt för Windows och Android. Ta som exempel fallet med 2 × 2-matrisen som tjänade oss för att illustrera Gauss-Seidel-metoden.

Lösning

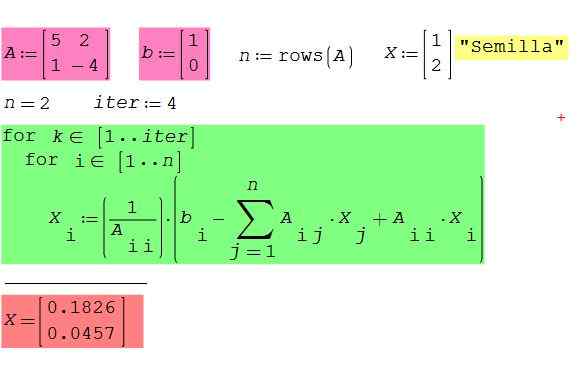figur 2. System för ekvationer i exempel 2 x 2, med programvara SMATH -studio. Källa: f. Zapata.

- Exempel 3

Applicera Gauss-seidel-algoritmen för följande 3 × 3-ekvationer, som tidigare har beställts på ett sådant sätt att de diagonala koefficienterna är dominerande (det vill säga med större absolut värde än de absoluta värdena på koefficienterna för koefficienterna av samma rad):

9 x1 + 2 x2 - x3 = -2

7 x1 + 8 x2 + 5 x3 = 3

3 x1 + 4 x2 - 10 x3 = 6

Använd nollvektorn som frö och överväga fem iterationer. Kommentera resultatet.

Lösning

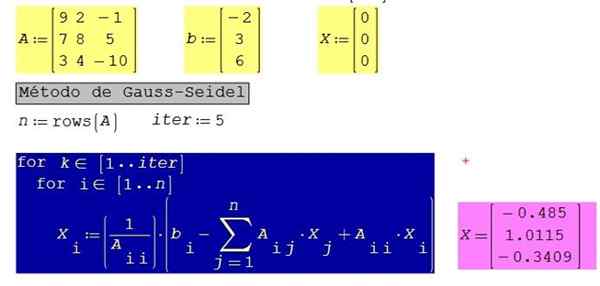Figur 3. Lösning av systemet för ekvationer i det upplösta exemplet 3, med SMATH -studio. Källa: f. Zapata.

För samma system med 10 iterationer istället för 5 Följande resultat erhålls: x1 = -0.485; X2 = 1.0123; X3 = -0.3406

Detta indikerar att det räcker med fem iterationer för att få tre precisionsdekimaler och att metoden snabbt förmedlar till lösningen.

- Exempel 4

Med hjälp av Gauss-Seidel-algoritmen, hitta lösningen på 4 × 4-ekvationssystemet som sker nedan:

10 x1 - x2 + 2 x3 + 0 x4 = 6

-1 x1 + 11 x2 - 1 x3 + 3 x4 = 25

2 x1 - 1 x2 + 10 x3 - 1 x4 = -11

0 x1 + 3 x2 - 1 x3 + 8 x4 = 15

För att starta metoden använder du detta frö:

x1 = 0, x2 = 0, x3 = 0 och x4 = 0

Tänk på 10 iterationer och uppskatta resultatet, jämför med iterationsnummer 11.

Lösning

Figur 4. Lösning av systemet för ekvationer i det upplösta exemplet 4, med SMATH -studio. Källa: f. Zapata.

Vid jämförelse med följande iteration (nummer 11) är resultatet identiskt. De största skillnaderna mellan de två iterationerna är i storleksordningen 2 × 10^-8, Vilket innebär att den visade lösningen har en noggrannhet på minst sju decimaler.

Referenser

1. Iterativa lösningsmetoder. Gauss-seidel. Återhämtat sig från: cimat.mx
2. Numeriska metoder. Gauss-seidel. Återhämtat sig från: test.Cua.Uam.mx
3. Numerisk: Gauss-Seidel-metoden. Återställt från: Lär dig i Linea.du.Edu.co
4. Wikipedia. Gauss-Seidel Method. Hämtad från: i. Wikipedia.com
5. Wikipedia. Gauss-Seidel Method. Återhämtad från: är.Wikipedia.com