Registrerad vinkel i en cirkeldefinition, sats, exempel

han Registrerad vinkel i en cirkel Det är den som har sitt toppunkt på omkretsen och dess halvtida är torra eller tangent till samma. Som en konsekvens kommer den registrerade vinkeln alltid att vara konvex eller platt.

I figur 1 representeras flera vinklar registrerade i respektive omkrets. Vinkeln ∠EDF är registrerad genom att ha sitt toppunkt på omkretsen och dess två semi -rekreer [av) och [df) torkar omkretsen. 

Figur 1. Flera inskrivna vinklar om sina respektive omkretsar. Källa: f. Zapata med geogebra.

På liknande sätt är vinkeln ∠HGI registrerad, för att ha sitt toppunkt i omkretsen och dess torra sidor till samma.

Vinklarna är också registrerade med omkretsen. Den första har en Secant -sida och den andra tangenten, medan den andra har sina två sidor tangent till omkretsen och bildar en platt planvinkel (180 °).

Vissa författare kallar en halvinskriven vinkel till den som har en av hans sidor tangent till omkretsen, men i den här artikeln anses han vara registrerad.

Eventuell registrerad vinkel definierar eller underhåller en båge associerad med samma. Till exempel i figur 2 undervisar den registrerade vinkeln ∠ABC bågen A⌒C av längd D.

Samma figur visar vinkeln ∠DOE, som inte är registrerad i omkretsen för att inte ha sitt toppunkt på sin omkrets, men i mitten eller.

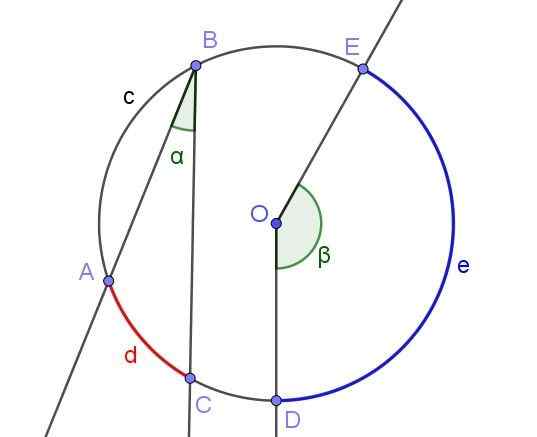figur 2. Registrerad vinkel ∠ABC och central vinkel ∠DOE. Källa: f. Zapata med geogebra.

[TOC]

Centralvinkel

Förutom den registrerade vinkeln, centralvinkel, vilket är den vars toppunkt är i mitten av omkretsen och vars sidor skär till omkretsen.

Kan tjäna dig: Skillnad mellan en gemensam fraktion och ett decimalnummer

Radianens mått på en central vinkel är kvoten mellan bågen som underlagar, det vill säga omkretsbågen mellan sidorna på vinkeln och omkretsens radie.

Om omkretsen är enhetlig (radie 1), är längden på bågen i samma radioenheter måtten på vinkeln i radianer.

Och när måtten på vinkeln krävs i grader multipliceras måtten i radianer med faktor 180º/π.

Vinklarna mätinstrument använder alltid en central vinkel och längden på bågen som är underlagd av detta direkt kalibrerat i grader. Detta innebär att när en vinkel mäts, i bakgrunden är det som mäts längden på bågen som är underlagd av den centrala vinkeln.

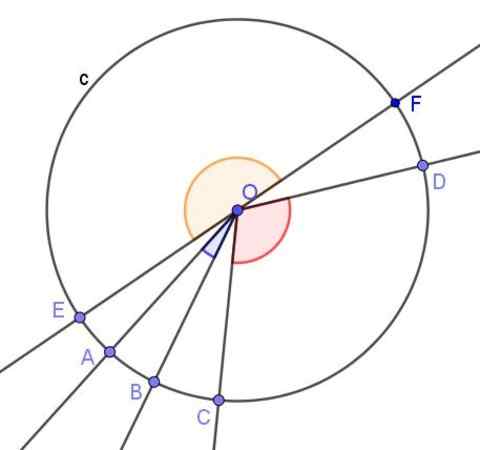Figur 3. Flera centrala vinklar i omkretsen. Källa: f. Zapata med geogebra.

Teorier

- Sats 1 (registrerad vinkel och central vinkel)

Måttet på en registrerad vinkel är hälften av måtten på den centrala vinkeln, om båda vinklarna subtiter samma båge.

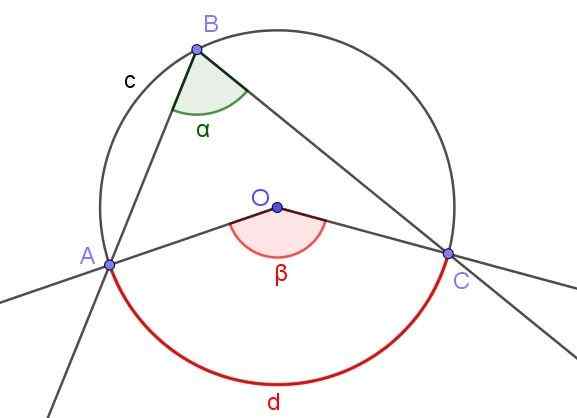Figur 4. Registrerad vinkel ∠ABC och central vinkel ∠AOC som subititerar samma båge A⌒C. Källa: f. Zapata med geogebra.

Figur 4 visar två vinklar ∠ABC och ∠AOC, som korsar samma omkretsbåge A⌒C.

Om måttet på den registrerade vinkeln är a, är p -måttet på den centrala vinkeln dubbelt så mycket som måttet på den registrerade vinkeln (β = 2 α) eftersom båda subtraherar samma uppmätta båge.

Demonstration 1

För att demonstrera sats 1 kommer flera speciella fall att börja, tills de når allmänt fallet.

Kan tjäna dig: Sandwich Law: Förklaring och övningar

Anta att en registrerad vinkel, där en av dess sidor passerar genom mitten av omkretsen, som visas i figur 5.

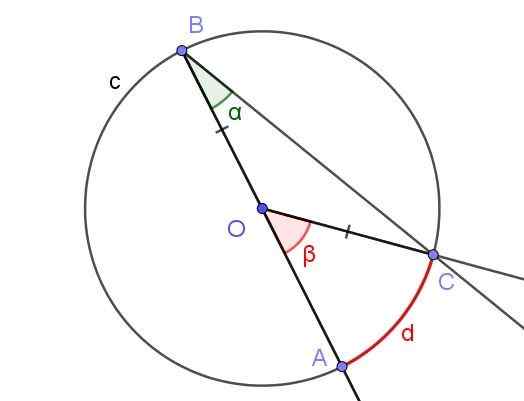Figur 5. Registrerad vinkel ∠ABC med sidan [BA) genom O och central vinkel ∠AOC. Källa: f. Zapata med geogebra.

I detta fall bildas Cob Isosceles Triange, eftersom [OC] = [OB].

I en isosceles triangel är vinklarna intill basen desamma, därför måste de ∠BCO = ∠ABC = α. Å andra sidan ∠COB = 180º - β.

Med tanke på summan av de inre vinklarna i kolvtriangeln du har:

α + α + (180º - β) = 180º

Där det följer att 2 α = β, eller vad som är motsvarande: α = ß/2. Detta sammanfaller med vad sats 1 säger: måttet på den registrerade vinkeln är hälften av den centrala vinkeln, om båda vinklarna lämnar in samma rep [AC].

Demonstration 1b

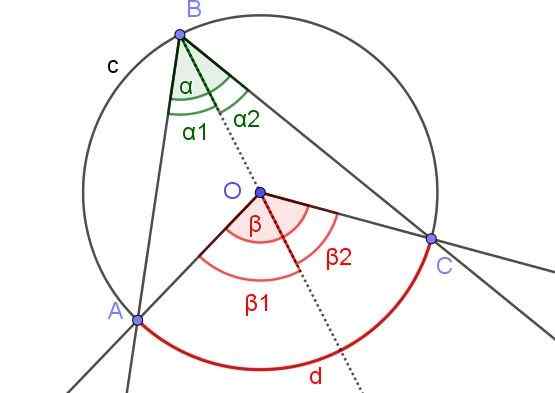Figur 6. Hjälpskonstruktion för att visa att a = β/2. Källa: f. Zapata med geogebra.

I det här fallet finns det en inskriven vinkel ∠ABC, där mitten eller omkretsen är inuti vinkeln.

För att demonstrera sats 1 i detta fall ritas det halvhögra hjälpen [BO), så att det finns två registrerade vinklar.

På samma sätt har de de centrala vinklarna ß₁ och β₂ intill nämnda semi -rekreation. På detta sätt har du samma situation som i demonstration 1, så det kan anges att α₂ = ß₂ /2 och a₁ = ß₁ /2. Som α = α₁ + a₂ och β = ß₁ + p₂ Det finns därför att α = α₁ + a₂ = ß₁ /2 + β₂ /2 = (β₁ + p₂) / 2 = β / 2.

Kan tjäna dig: typer av integraler

Sammanfattningsvis a = β / 2, som uppfyller sats 1.

- Sats 2

Om två eller flera registrerade vinklar undervisar samma båge, har de samma mått.

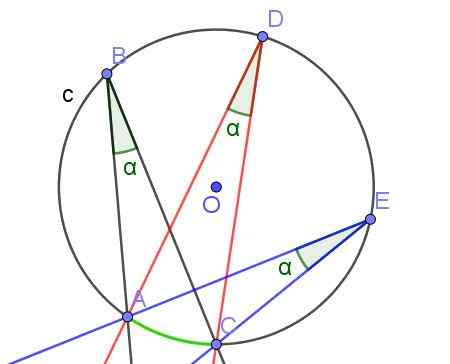Figur 7. Registrerade vinklar med lika mått α, eftersom de underkastar samma båge A⌒C. Källa: f. Zapata med geogebra.

- Sats 3

De registrerade vinklarna undervisar det finns strängar av samma mått är desamma.

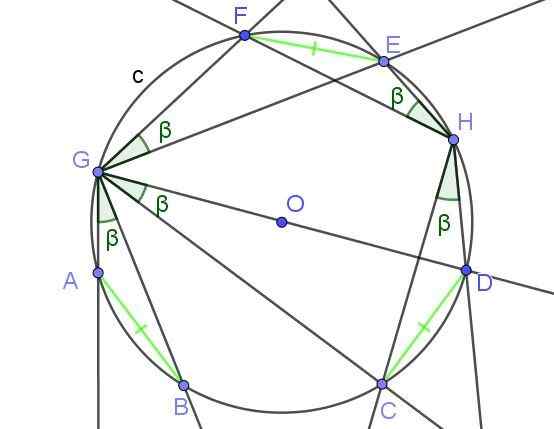Figur 8. De inskrivna vinklarna som subtusar rep med lika mått har lika mått ß. Källa: f. Zapata med geogebra.

Exempel

- Exempel 1

Visa att den inskrivna vinkeln subtiter diametern är en rätt vinkel.

Lösning

Den centrala vinkeln ∠AOB associerad med diameter är en platt vinkel, vars mått är 180º.

Enligt sats 1 har valfri vinkel registrerad i omkretsen som underkastar samma rep (i detta fall diametern), som mäter hälften av den centrala vinkeln som subtiterar samma rep, som för vårt exempel är 180º/2 = 90º.

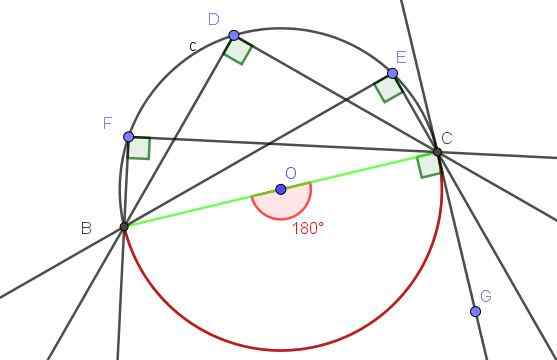Figur 9. Varje registrerad vinkel som underlag till diameter är en rätt vinkel. Källa: f. Zapata med geogebra.

- Exempel 2

Linjen (BC) tangent i A A till omkrets C, bestämmer den inskrivna vinkeln ∠BAC (se figur 10).

Verifiera att sats 1 i de registrerade vinklarna är uppfyllda.

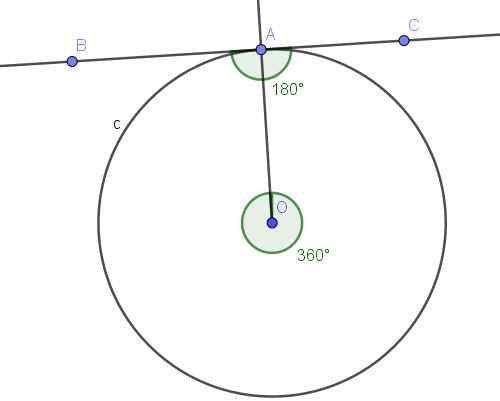Figur 10. Registrerad vinkel BAC och dess konvexa centrala vinkel AOA. Källa: f. Zapata med geogebra.

Lösning

Vinkeln ∠BAC är registrerad eftersom dess toppunkt är på omkretsen, och dess sidor [AB) och [AC) är tangent för omkretsen, så definitionen av inskriven vinkel uppfylls.

Å andra sidan underkastar den inskrivna vinkeln ∠BAC A⌒A -bågen, som är den fullständiga omkretsen. Den centrala vinkeln som underhåller A⌒A -bågen är en konvex vinkel vars mått är full vinkel (360º).

Den registrerade vinkeln subtiter hela bågen mäter hälften av den tillhörande centrala vinkeln, det vill säga ∠BAC = 360º/2 = 180º.

Med allt ovan är det bevisat att detta specifika fall uppfyller sats 1.

Referenser

1. Baldor. (1973). Geometri och trigonometri. Centralamerikansk kulturell redaktion.
2. OCH. TILL. (2003). Geometrielement: med övningar och kompassgeometri. University of Medellin.
3. Geometri 1st. Vinklar i omkretsen. Återhämtat sig från: edu.Xunta.är/
4. All vetenskap. Föreslagna övningar av vinklar i omkretsen. Återhämtat sig från: FrancesPhysics.Bloggfläck.com
5. Wikipedia. Registrerad vinkel. Återhämtad från: är.Wikipedia.com