Interna och externa konjugerade vinklar exempel, övningar

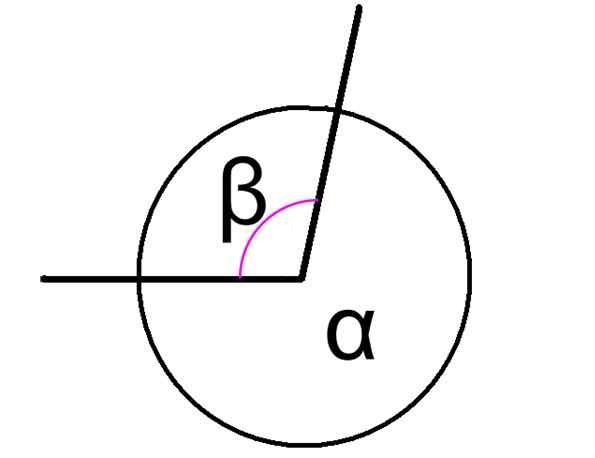
De konjugerade vinklar Det är de som läggs till som ett resultat av 360 °, oavsett om dessa vinklar är intilliggande eller inte. Figur 1 visar två konjugerade vinklar, betecknade som a och ß.

I så fall har vinklarna α och ß i figuren ett vanligt toppunkt och deras sidor är vanliga, därför är de intilliggande. Förhållandet mellan dem uttrycks enligt följande:

α + β = 360º

Figur 1. Två konjugerade centrala vinklar, summan. Källa: Wikimedia Commons. Ingen maskinläsbar författare tillhandahållen. Thiago R Ramos antog (baserat på upphovsrättsanspråk). [CC BY-SA 3.0 (http: // Creativecommons.Org/licenser/BY-SA/3.0/)] det är en klassificering av vinklarna med dess summa. Andra viktiga definitioner inkluderar kompletterande vinklar, vars summa är 90 º och kompletterande vinklar, som uppgår till 180 º.

Å andra sidan, låt oss nu överväga två parallella linjer som klipps av en sekant, vars disposition visas då:

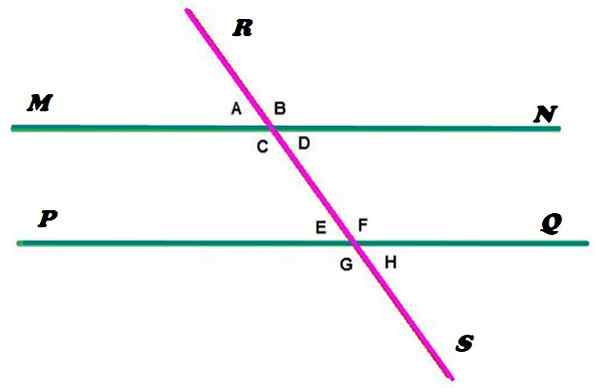figur 2. Parallella linjer klippta av en sekant. Källa: f. Zapata.

MN- och PQ -linjerna är parallella, medan RS -linjen torkar, korsar paralleller i två punkter. Som man kan se bestämmer denna konfiguration bildningen av 8 vinklar, till vilken den har betecknats med små bokstäver.

Tja, enligt definitionen i början är vinklar A, B, C och D konjugerade. Och på samma sätt som de är E, F, G och H, eftersom båda fallen är uppfyllda att:

A+B+C+D = 360º

OCH

E+F+G+H = 360º

För denna konfiguration konjugeras två vinklar om de är på samma sida med avseende på RS -torklinjen och båda är interna eller externa. I det första fallet talas vinklar Interna konjugat, Medan de är i den andra är de vinklar extern konjugat.

[TOC]

Exempel

I figur 2 är de yttre vinklarna de som ligger utanför regionen avgränsade av MN- och PQ -linjerna, det är vinklarna A, B, G och H. Medan vinklarna som är mellan de två linjerna är C, D, E och F.

Kan tjäna dig: Coplanares Points: Ekvation, exempel och lösta övningar

Nu är det nödvändigt att analysera vilka vinklar som är till vänster och vilken till höger om Secant.

Till vänster om Rs är vinklar A, C, E och G. Och till höger är B, D, F och H.

Vi fortsätter omedelbart för att bestämma paren av konjugerade vinklar, enligt definitionen som anges i föregående avsnitt:

-A och G, extern och till vänster om Rs.

-D och f, inre och till höger om Rs.

-B och H, extern och till höger om Rs.

-C och E, interna och till vänster om Rs.

Egenskap av konjugerade vinklar mellan parallella linjer

De konjugerade vinklarna mellan parallella linjer är kompletterande, det vill säga deras summa är lika med 180 °. På detta sätt, för figur 2, uppfylls följande:

A + G = 180º

D + f = 180º

B + H = 180º

C + E = 180º

Motsvarande vinklar par för parallella linjer

De är de som är på samma sida av torklinjen, de är inte intilliggande och en av dem är inre och den andra är extern. Det är viktigt att visualisera dem, eftersom deras mått är densamma, eftersom de är motsatta vinklar av toppunkten.

Återvända till figur 2 identifieras motsvarande vinklar som:

-A och e

-C och g

-B och f

-D och h

Inre vinklar i en fyrkantig

Kvadrilateralerna är 4 -sidiga polygoner, inklusive torget, rektangeln, trapes, parallellogrammet och romben, till exempel. Oavsett dess form är det i någon av dem uppfyllt att summan av dess inre vinklar är 360º, därför följer de definitionen i början.

Låt oss titta på några exempel på fyrkantiga och hur man beräknar värdet dess inre vinklar enligt informationen i föregående avsnitt:

Kan tjäna dig: Vilka är de sju elementen i omkretsen?

Exempel

a) Tre av vinklarna i ett fyrkantigt mått 75º, 110º och 70º. Hur mycket ska den återstående vinkeln mäta?

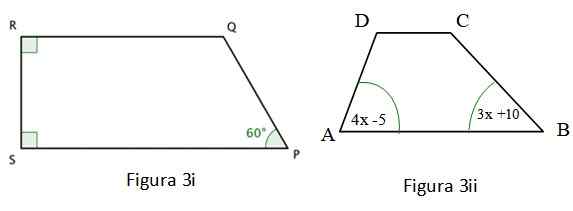
b) Hitta värdet på vinkeln ∠Q i figur 3 i.

c) Beräkna hur mycket mäter vinkeln ∠A i figur 3 II.

Lösning till

Låt α vara den saknade vinkeln, det uppfylls att:

α + 75 º + 110º + 70º = 360 → α = 105º

Lösning B

Figur 3i som visas är en Trapezoid Och två av dess inre vinklar är raka, som har påpekats med en färgkorg i hörnen. För denna fyrkantiga verifieras följande:

∠R + ∠S + ∠P + ∠Q = 360º; ∠S = ∠R = 90º; ∠P = 60º

Därför:

∠ Q = 2 x 90º + 60º = 240º

Lösning C

Kvadrilateralen i figur 3 II är också en trapes, för vilken följande är uppfyllt:

∠A + ∠B + ∠C + ∠D = 360º

Därför:

4x -5 + 3x + 10 +180 = 360

7x + 5 = 180

X = (180 - 5) / 7

x = 25

För att bestämma den begärda vinkeln i uttalandet används det att ∠A = 4x - 5. Ersätta värdet på X tidigare beräknat följs att ∠A = (4 × 25) -5 = 95º

Övningar

- Övning 1

Att veta att en av de visade vinklarna är värt 125, att hitta måtten på de återstående 7 vinklarna i följande figur och motivera svaren.

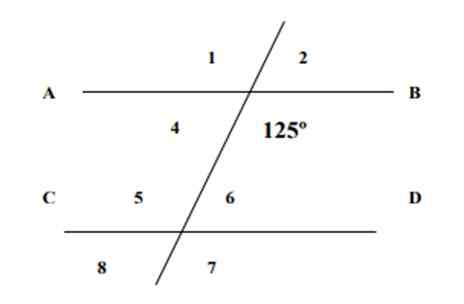Figur 4. Linjerna och vinklarna i övning 1. Källa: f. Zapata.

Lösning

Vinkel 6 och vinkel 125 är inre konjugat, vars summa är värd 180º, enligt egenskapen hos de konjugerade vinklarna, därför:

∠6 + 125º = 180º → ∠6 = 180º - 125º = 55º

Å andra sidan ∠6 och ∠8 är motsatta vinklar av toppen, vars mått är densamma. Därför mäter ∠8 55º.

Kan tjäna dig: vektoralgebra

Vinkeln ∠1 motsätter sig också av toppen vid 125, då kan vi bekräfta att ∠1 = 125º. Vi kan också vädja till det faktum att motsvarande vinklar har samma mått. I figuren är dessa vinklar:

∠7 = 125 °

∠2 = ∠6 = 55 °

∠1 = ∠5 = 125º

∠4 = ∠8 = 55 °

- Övning 2

Hitta värdet på X i följande figur och värdena på alla vinklar:

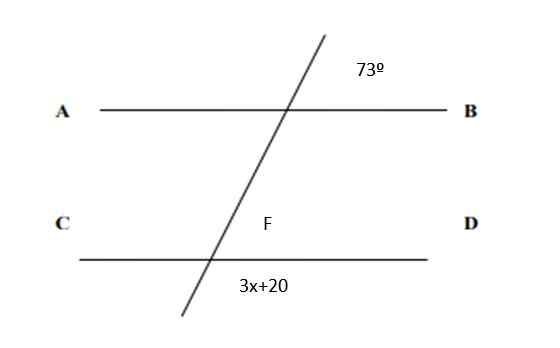Figur 5. Linjer och vinklar för övning 2. Källa: f. Zapata.

Lösning

Eftersom de är motsvarande par följer det att f = 73º. Och å andra sidan är summan av de konjugerade paren 180º därför:

3x + 20º + 73º = 180º

3x = 180º - 73º -20º = 87

Slutligen är värdet på X:

x = 87/3 = 29

När det gäller alla vinklar visas de listade i följande figur:

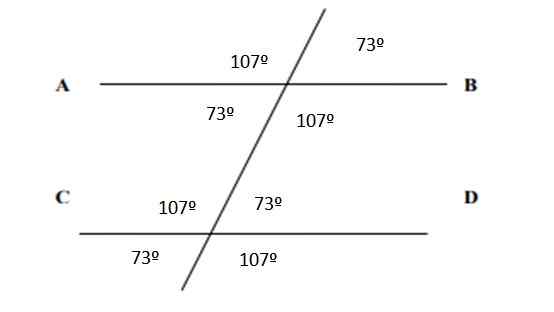Figur 6. Vinklar som resulterar i övning 2. Källa: f. Zapata.

Referenser

1. Vinkelgrupper. Kompletterande, kompletterande och explementära vinklar förklaring. Återhämtat sig från: Thisiget.com/
2. Baldor, a. 1983. Flat och rymd- och trigonometri -geometri. Kulturhem.
3. Corral, m. Matematik Librettexts: Vinklar. Återhämtat sig från: matematik.Librettexts.org.
4. Mathmania. Klassificera och konstruera vinklar genom deras mätning. Återhämtat sig från: Mathemania.com/
5. Wentworth, g. Planetgeometri. Återhämtat sig från: Gutenberg.org.
6. Wikipedia. Konjugerade vinklar. Återhämtad från: är.Wikipedia.org.