Coplanares punkter Ekvation, exempel och löst övningar

De Coplanares poäng De tillhör alla samma plan. Två punkter är alltid coplanarer, eftersom dessa punkter definierar en linje genom vilken platt oändliga passerar. Sedan tillhör båda punkterna var och en av de planer som passerar genom linjen och därför alltid kommer att vara Coplanares.

Å andra sidan definierar tre punkter ett enda plan, av vilket det följs att tre punkter alltid kommer att vara coplanares till det plan de bestämmer.

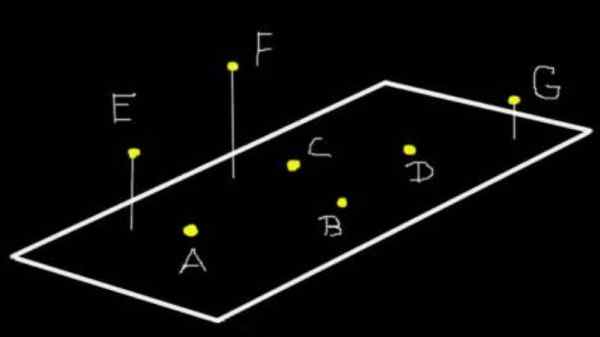
Figur 1. A, B, C och D De är coplanares till planet (ω). E, f och g är inte coplanares a (ω) men om de är coplanares till planet som tre definierar. Källa: f. Zapata.

Mer än tre poäng kan vara coplanar eller inte. Till exempel i figur 1 är punkterna A, B, C och D coplanares till planet (ω). Men E, F och G är inte Coplanares A (ω), även om de är coplanares till planet som tre definierar.

[TOC]

Ekvation av ett plan som ges tre poäng

Ekvationen för ett plan bestämd av tre kända punkter a, b, c är en matematisk relation som garanterar att någon punkt p av generiska koordinater (x, y, z) som uppfyller ekvationen tillhör nämnda plan. 

Det föregående uttalandet motsvarar att säga att om p av koordinat (x, y, z) uppfyller planekvationen, då kommer den nämnda punkten att vara till copatar med de tre punkterna a, b, c som bestämde planet.

För att hitta ekvationen i nämnda plan, låt oss börja med att hitta vektorerna Ab och Växelström:

Ab = [BX - Ax, av - Ay, BZ - AZ]

Växelström = [CX - AX, CY - AY, CZ - AZ]

Vektorprodukten Ab X Växelström Det resulterar i en vinkelrätt eller normal vektor till planet bestämd av punkterna A, B, C.

En vilken punkt med koordinater (x, y, z) tillhör planet om det är sant att vektorn Ap är vinkelrätt mot vektorn Ab X Växelström, vilket är garanterat om det är uppfyllt:

Kan tjäna dig: Decagon: Regelbundet, oregelbundet, egenskaper, exempel

AP • (AB X Ac) = 0

Detta motsvarar att säga att trippelprodukten av Ap, Ab och Växelström Vara noll. Den föregående ekvationen kan skrivas på ett matris sätt:

Exempel

Låt poäng A (0, 1, 2); B (1, 2, 3); C (7, 2, 1) och D (till, 0, 1). Vilket värde ska ha till så att de fyra punkterna är coplanares?

Lösning

För att hitta värdet på A är det nödvändigt att punkten D är en del av planet bestäms av A, B och C, vilket garanteras om planekvationen uppfyller.

Utveckla den avgörande faktor vi har:

A (-1-1) + 1 (-1 -7) -1 (1 -7) = -2A -8 + 6 = -2A -2 = 0

Den tidigare ekvationen indikerar det A = -1 För att uppfylla jämlikhet. Med andra ord, det enda sättet D (till, 0.1) vara coplanar med punkterna a, b och c är det till Valga -1. Annars kommer det inte att vara coplanar.

Löst övningar

- Övning 1

Ett plan korsar de kartesiska axlarna x, y, z i 1, 2 respektive 3. Korsningen mellan nämnda plan med axlarna bestämmer punkterna a, b och c. Hitta DZ -komponenten i en punkt D, vars kartesiska komponenter är:

 D (-DZ, DZ+1, DZ) 

Under förutsättning att d är coplanar med punkter a, b och c. 

Lösning

När avlyssningarna av ett plan med de kartesiska axlarna är kända kan den segmentella formen för planekvationen användas:

x/1 + y/2 + z/3 = 1

Eftersom punkt D måste tillhöra det tidigare planet måste du:

-Dz/1 + (dz + 1)/2 + dz/3 = 1

Det vill säga:

-DZ + DZ/2 + ½ + DZ/3 = 1

Dz (-1 + ½ + ⅓) = ½ 

Dz (-1/6⅙) = ½ 

DZ = -3 

Från ovanstående följer den punkten D (3, -2, -3) är att koppla med punkterna A (1, 0, 0); B (0, 2, 0) och C (0, 0, 3).

Det kan tjäna dig: triangulösa likhetskriterier

- Övning 2

Bestämma om punkterna A (0, 5, 3); B (0, 6, 4); C (2, 4, 2) och D (2, 3, 1) är coplanares.

Lösning

Vi bildar matrisen vars rang är koordinaterna för D-A, B-A och C-A. Då beräknas determinanten och den verifieras om noll eller inte.

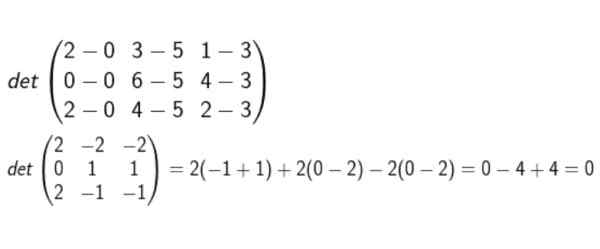
Efter att ha utfört alla beräkningar dras slutsatsen att de är Coplanares.

- Övning 3

Två rader ges i rymden. En av dem är linjen (R) vars parametriska ekvation är:

(R): x = 1 + 2 λ; y = 1 - λ; Z = 1

Och den andra är linjen (er) vars ekvation är:

(S): x + 2 y = 1; Z = -1

Demonstrera att (r) och (er) de är coplanarium raka, det vill säga de är i samma plan.

Lösning

Låt oss starta godtyckligt två punkter på linjen (R) och två på linjen (er):

Rak (r): λ = 0; A (1, 1, 1) och λ = 1; B (3, 0, 1)

Låt oss göra x = 0 på linjen=> y = ½; C (0, ½, -1). Och å andra sidan, om vi gör det y = 0 => x = 1; D (1, 0, -1).

Det vill säga, vi har tagit poäng A och B som tillhör linjen (R) och punkterna C och D som tillhör linjen (S). Om dessa punkter är Coplanares, kommer de två linjerna också att vara.

Nu väljer vi att peka på hur pivoten och sedan hittar vi koordinaterna för vektorerna Ab, Växelström och Annons. På detta sätt får du:

B - A: (3-1, 0 -1, 1 - 1) => Ab= (2, -1, 0)

C -a: (0-1, 1/2 -1, -1 -1) => Växelström= (-1, -1/2, -2)

D -a: (1-1, 0 -1, -1 -1) => Annons= (0, -1, -2)

Nästa steg är att bygga och beräkna determinanten vars första rad är vektorkoefficienterna Ab, Den andra raden är de av Växelström och den tredje raden för vektorn Annons:

Kan tjäna dig: Miletus sådan teorem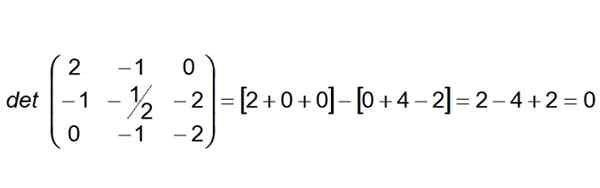

Eftersom determinanten visar sig vara noll, kan vi dra slutsatsen att de fyra punkterna är coplanarios. Dessutom kan det sägas att linjer (R) och (er) också är Coplanares.

- Övning 4

Linjerna (r) och (er) är coplanares, vilket visas i övning 3. Hitta ekvationen för planet som innehåller dem.

Lösning

Poäng A, B, C definierar helt det planet, men vi vill införa att alla punktar X av koordinater (X, Y, Z) tillhör samma.

X - A: (X -1, Y -1, Z - 1) => Yxa= (X -1, y -1, z -1)

B - A: (3-1, 0 -1, 1 - 1) => Ab= (2, -1, 0)

C -a: (0-1, 1/2 -1, -1 -1) => Växelström= (-1, -1/2, -2)

Så att X tillhör det plan som definierats av A, B, C och i vilka linjerna (R) och (er) finns, är det nödvändigt att den determinanten som bildas i sin första rad upphävs av komponenterna i Yxa, i den andra av de av Ab Och i det tredje av de av Växelström:

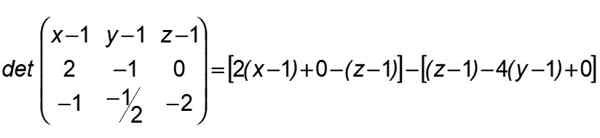
Efter detta resultat grupperar vi på detta sätt:

2 (x-1) + 4 (y-1) -2 (z-1) = 0

Och omedelbart ser det att det kan skrivas om så här:

x - 1 + 2y - 2 - z + 1 = 0

Därför x + 2y - z = 2 är ekvationen för planet som innehåller linjerna (r) och (er).

Referenser

1. Fleming, w. 1989. Prealculus matematik. Prentice Hall PTR.
2. Kolman, f. 2006. Linjär algebra. Pearson Education.
3. Lojal, j. M. 2005. Platt analytisk geometri. Mérida - Venezuela: Venezuelansk redaktion C. TILL.
4. Navarro, Rocio. Vektorerna. Återhämtat sig från: böcker.Google.co.gå.
5. Pérez, c. D. 2006. Förkalkning. Pearson Education.
6. Prenowitz, w. 2012. Grundläggande geometri. Rowman & Littlefield.
7. Sullivan, m. 1997. Förkalkning. Pearson Education.