Vinklar i omkretsstyper, egenskaper, övningar löst

Kallad Omkretsvinklar till de där något av dess element är eller korsar vid en given omkrets. Bland dem är följande:

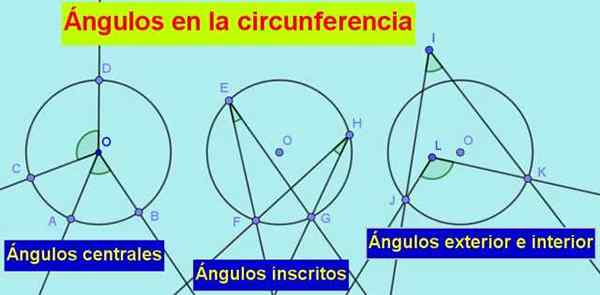
1.- han centralvinkel, vars toppunkt är i mitten av omkretsen och dess sidor torkar till det, som vi ser i följande bild:

Figur 1. Typen av vinklar i omkretsen är: det centrala, det inskrivna, utsidan och det inre. Källa: f. Zapata.

2.- han registrerad vinkel, vars toppunkt är på omkretsen och dess sidor är torra eller tangent till omkretsen.

3.- Yttre vinkel, vars toppunkt är ur omkretsen men sidorna är torra eller tangent till omkretsen.

4.- han Innervinkel, med toppunktet i omkretsen och dess torra sidor till samma.

Alla dessa vinklar håller vissa relationer med varandra och detta leder oss till viktiga egenskaper mellan vinklarna som tillhör en given omkrets.

[TOC]

Egenskaper

- Centralvinkel

Den centrala vinkeln definieras som den vars toppunkt är i mitten av omkretsen och dess sidor skärs i omkretsen.

Radianens mått på en central vinkel är kvoten mellan bågen som underlagar, det vill säga omkretsbågen mellan sidorna på vinkeln och omkretsens radie. 

Om omkretsen är enhetlig, det vill säga radie 1, är måtten på den centrala vinkeln längden på bågen, vilket motsvarar antalet radianer.

Om du vill ha måtten på den centrala vinkeln i grader multipliceras måtten i radianer med faktor 180º/π.

Vinklarna mätinstrument, såsom transportören och goniometern, använder alltid en central vinkel och längden på den subventionerade bågen.

Kan tjäna dig: partiella derivat: egenskaper, beräkning, övningar

De är kalibrerade i sexagesimala grader, vilket innebär att när en vinkel mäts med dem, i ryggen är det som mäts längden på bågen som är underlagd av den centrala vinkeln.

Fast egendom

Måttet på en central vinkel i radianer är lika med längden på bågen som subtiner eller avlyssningar divideras med radie längd.

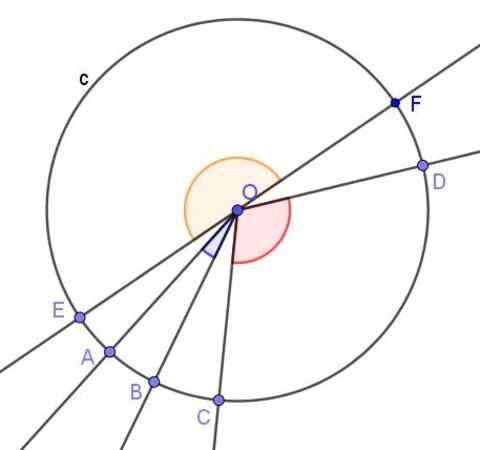figur 2. Tre centrala vinklar visas. En akut, den andra stöt och en platt. Källa: f. Zapata.

- Registrerad vinkel

Den registrerade vinkeln på en omkrets är en som har sitt toppunkt på omkretsen och dess halvtida är torra eller tangent till samma. 

Dess egenskaper är:

Egenskaper

-Den registrerade vinkeln är konvex eller platt.

-När en inskriven vinkel avlyssnar samma båge som den centrala vinkeln, kommer måttet på den första att vara hälften av den andra.

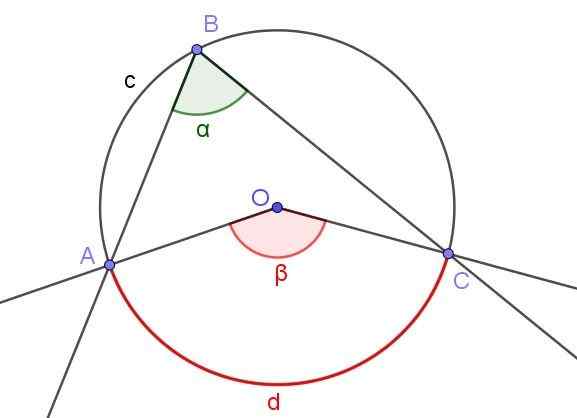Figur 3. Registrerad vinkel ∠ABC och central vinkel ∠AOC som subititerar samma båge A⌒C. Källa: f. Zapata.

Figur 3 visar två vinklar ∠ABC och ∠AOC som avlyssnar samma omkretsbåge.

Om måttet på den registrerade vinkeln är a, är p -måttet på den centrala vinkeln dubbelt så mycket som måttet på den registrerade vinkeln (β = 2 α) eftersom båda subtraherar samma uppmätta båge.

- Yttre vinkel

Det är vinkeln vars toppunkt ligger utanför omkretsen och var och en av dess sidor skär till omkretsen i en eller flera punkter.

Fast egendom

-Måttet är lika med semi -express (eller skillnad dividerat med 2) av de centrala vinklarna som avlyssnar själva bågarna.

För att säkerställa att måttet är positivt bör semi -expressen alltid vara den centrala vinkeln för den största måtten mindre måttet på den nedre centrala vinkeln, såsom illustreras i följande figur.

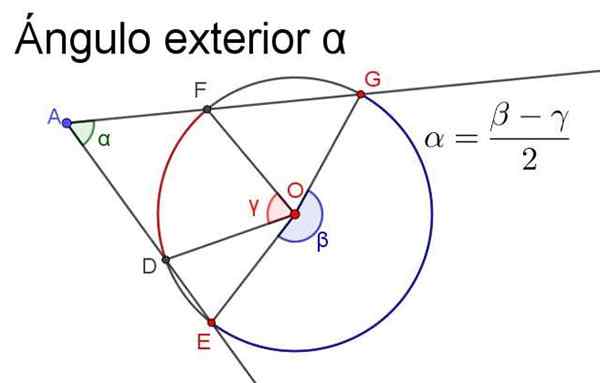Figur 4. Den yttre vinkeln α är lika med halvreferensen för centralerna som underkastar samma bågar. Källa: f. Zapata.

- Innervinkel

Den inre vinkeln är den vars toppunkt är inne i omkretsen och dess sidor skärs till omkretsen.

Kan tjäna dig: Bestämningskoefficient: Formler, beräkning, tolkning, exempel

Fast egendom 

Måttet är lika med halv -gruppen i den centrala vinkeln som underkastar samma båge, plus den centrala vinkeln som underkastar samma båge som dess förlängningsvinkel (detta är den inre vinkeln som bildas av semi -strängen komplementär till originalet inre vinkel).

Följande figur illustrerar och klargör egenskapen hos den inre vinkeln.

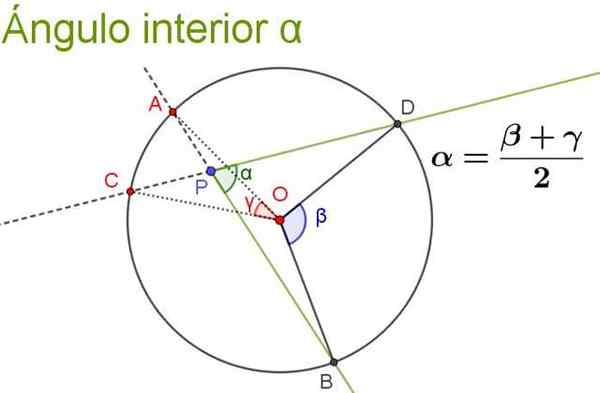Figur 5. Den inre vinkeln är lika med semi -seismumet i de centrala vinklarna som underkastar samma bågar som han själv. Källa: f. Zapata.

Löst övningar

- Övning 1

Anta en inskriven vinkel där en av dess sidor passerar genom omkretsens centrum, som visas i figur 6. Omkretsens radie är OA = 3 cm och bågen har en längd på π/2 cm. Bestäm värdet på α- och ß -vinklar.

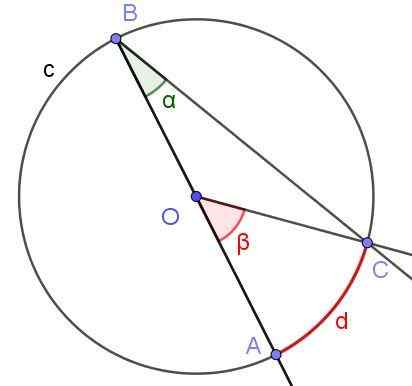Figur 6. Registrerad vinkel ∠ABC med sidan [BA) genom O och central vinkel ∠AOC.Källa: f. Zapata.

Lösning

I detta fall bildas Cob Isosceles Triange, eftersom [OC] = [OB]. I en isosceles -triangel är vinklarna intill basen desamma, därför måste de ∠BCO = ∠ABC = α. Å andra sidan ∠COB = 180º - β. Med tanke på summan av de inre vinklarna i kolvtriangeln du har:

α + α + (180º - β) = 180º

Från där det följer att 2 α = β, eller vad som är motsvarande a = ß/2, vilket bekräftar egenskapen (3) i föregående avsnitt, att måttet på den registrerade vinkeln är hälften av den centrala vinkeln, när båda vinklarna subtraherar samma rep [AC].

Nu fortsätter vi med att bestämma de numeriska värdena: ß -vinkeln är central och dess mått i radianer är förhållandet mellan bågen D och radien R = OA, så dess mått är:

β = d / r = (π / 2 cm) / (3 cm) = π / 6 rad = 30º.

Kan tjäna dig: fyrkantig: element, egenskaper, klassificering, exempel

Å andra sidan hade det redan bekräftats att α = β / 2 = (π / 6 rad) / 2 = π / 12 rad = 15º. 

- Övning 2

I figur 7 är vinklarna α₁ och β₂ har samma åtgärd. Dessutom vinkeln ß₁ Den mäter 60º. Bestämma vinklarna ß och a.

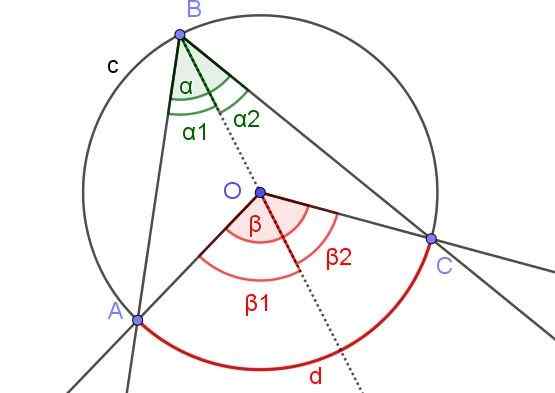Figur 7. I figur a₁ = ß₂ och β₁ = 60º. Bestämma värdena på p och a. Källa: f. Zapata.

Lösning

I det här fallet finns det en inskriven vinkel ∠ABC där mitten eller omkretsen är inuti vinkeln.

På grund av egendom (3) har du α₂ = ß₂ /2 och a₁ = ß₁ /2. Som:

α = α₁ + a₂ och β = ß₁ + p₂

Du har därför:

α = α₁ + a₂ = ß₁ /2 + β₂ /2 = (β₁ + p₂) / 2 = β / 2.

Det vill säga enligt egenskaperna:

α = β / 2

Som vi får höra att ß₁ = 60º då:

a₁ = ß₁ / 2 = 60º / 2 = 30º.

De berättar också för oss att α₁ = ß₂ Så det följer det:

p₂ = 30º.

Vinkeln ß är:

p₁ + p₂ = 60º + 30º = 90º +.

Och som α = β / 2, då:

α = 90º / 2 = 45º. 

Sammanfattningsvis:

β = 90º och a = 45º.

Referenser

1. Baldor, a. 1973. Geometri och trigonometri. Centralamerikansk kulturell redaktion.
2. OCH. TILL. 2003. Geometrielement: med övningar och kompassgeometri. University of Medellin.
3. Geometri 1st. Vinklar i omkretsen. Återhämtat sig från: edu.Xunta.är.
4. All vetenskap. Löst övningar av vinklar i omkretsen. Återhämtat sig från: FrancesPhysics.Bloggfläck.com
5. Wikipedia. Registrerad vinkel. Återhämtad från: är.Wikipedia.com