Rationella siffror egenskaper, exempel och operationer

De rationella nummer De är alla siffror som kan erhållas som uppdelning av två hela siffror. Exempel på rationella nummer är: 3/4, 8/5, -16/3 och de som visas i följande figur. I ett rationellt nummer anges kvoten, att vara möjlig att göra det senare vid behov.

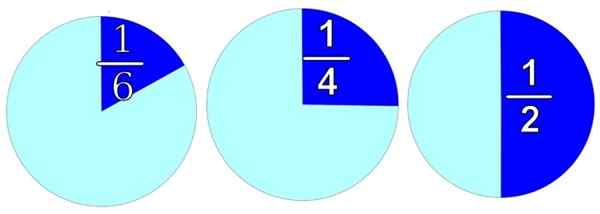
I figuren är alla objekt representerade, runda för komfort. Om vi ​​vill dela upp den i två lika delar, som till höger, har vi två halvor och var och en är 1/2.

Figur 1. Rationella siffror används för att dela upp hela i olika delar. Källa: FreeSVG.

Genom att dela upp den i 4 lika delar kommer vi att få 4 stycken och var och en är värd 1/4, som i bilden av mitten. Och om du måste distribuera den i 6 lika delar, skulle varje del vara värd 1/6, vilket vi ser på bilden till vänster.

Naturligtvis kan vi också dela upp det i två icke -lika delar, till exempel kan vi hålla 3/4 delar och spara 1/4 del. Andra avdelningar är också möjliga, till exempel 4/6 delar och 2 delar. Det viktiga är att summan av alla delar är 1.

På detta sätt är det uppenbart att med rationella siffror kan du dela, räkna och distribuera saker som mat, pengar, mark och alla slags föremål i bråkdelar. Och så är mängden verksamhet som kan göras med siffrorna utökat.

Rationella siffror kan också uttryckas decimalt, vilket kan ses i följande exempel:

1/2 = 0,5

1/3 = 0,3333 ..

3/4 = 0,75

1/7 = 0.142857142857142857 ..

Senare anger vi hur man går från ett sätt till ett annat med exempel.

[TOC]

Rationella siffror egenskaper

De rationella siffrorna, vars uppsättning vi kommer att beteckna med bokstaven Q, har följande egenskaper:

-Q inkluderar naturliga nummer n och hela n nummer.

Med hänsyn till att valfritt nummer till Det kan uttryckas som kvoten med varandra och 1, det är lätt att se att det också finns naturliga siffror och heltal.

Således kan det naturliga nummer 3 skrivas som en bråkdel, och även -5:

3 = 3/1

-5 = -5/1 = 5/-1 = -(5/1)

På detta sätt är det en numerisk uppsättning som täcker ett större antal siffror, något mycket nödvändigt, lägg de "runda" siffrorna inte tillräckligt för att beskriva alla möjliga operationer att göra.

Kan tjäna dig: 90 delare: vad är och förklaring

-Rationella siffror kan läggas till, subtraheras, multiplicera och dela, resultatet av att operationen är ett rationellt nummer: 1/2 + 1/5 = 7/10; 1/2 - 1/5 = 3/10; (1/2) x (1/5) = 1/10; (1/2) ÷ (1/5) = 5/2.

-Mellan varje par rationella nummer kan ett annat rationellt nummer alltid hittas. Faktum är att mellan två rationella siffror finns det rationella oändliga. 

Till exempel är mellan rationella 1/4 och 1/2 rationella 3/10, 7/20, 2/5 (och många fler), vilket kan verifieras och uttrycka dem som decimaler.

-Varje rationellt antal kan uttryckas som: i) ett heltal eller ii) en begränsad decimal (strikt) eller tidning: 4/2 = 2; 1/4 = 0,25; 1/6 = 0.1666666 ..

-Samma nummer kan representeras av oändliga motsvarande fraktioner och alla tillhör Q. Låt oss titta på den här gruppen:

Alla representerar decimalen 0.428571 ..

-Bland alla motsvarande fraktioner som representerar samma nummer är den oåterkalleliga fraktionen, den enklaste av alla, Kanonisk representant av det numret. Den kanoniska representanten för föregående exempel är 3/7.

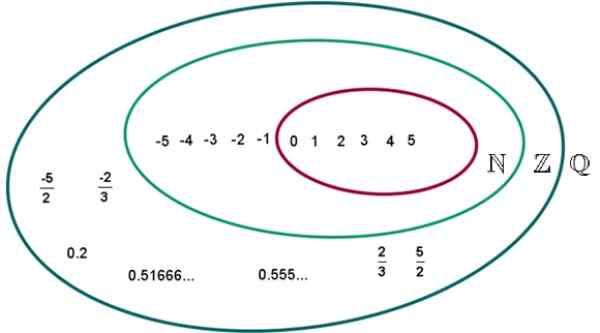figur 2.- Q -uppsättningen av rationella siffror. Källa: Wikimedia Commons. UVM Eduardo Artur/CC BY-S (https: // Creativecommons.Org/licenser/BY-SA/4.0).

Exempel på rationella siffror

-Egna fraktioner, de där telleren är mindre än nämnaren:

-Felaktiga fraktioner, vars teller är större än nämnaren:

-Naturliga siffror och hela siffror:

-Motsvarande fraktioner:

Decimalrepresentation av ett rationellt antal

När telleren är uppdelad mellan nämnaren är decimalformen för det rationella antalet. Till exempel:

2/5 = 0.4

3/8 = 0.375

1/9 = 0.11111 ..

6/11 = 0.545454 ..

I de två första exemplen är mängden decimaler begränsad. Detta innebär att när divisionen görs erhålls en vila.

Å andra sidan, under de kommande två, är antalet decimaler oändligt och det är därför de suspensiva punkterna placeras. I det senare fallet finns ett mönster i decimalerna. När det gäller fraktion 1/9 upprepas figur 1 på obestämd tid, medan den i 6/11 är 54.

Det kan tjäna dig: frekvens sannolikhet: koncept, hur det beräknas och exempel

När detta händer sägs det att decimalen är tidning och betecknas med circumflex -accent enligt följande:

Förvandla en decimal till fraktion

Om det är en begränsad decimal elimineras komma helt enkelt och nämnaren blir enheten följt av så många nollor som siffror har decimalen. Till exempel för att omvandla decimal 1.26 I fraktion är det skrivet så här:

1.26 = 126/100

Sedan förenklas den resulterande fraktionen till maximalt:

126/100 = 63/50

Om decimalen är obegränsad först är perioden identifierad. Sedan följs dessa steg för att hitta den resulterande fraktionen:

-Siffran är subtraktionen mellan antalet (ingen koma eller circumflex -accent) och den del som inte bär circumflex -accenten.

-Nämnaren är ett heltal med så många 9 som siffror som finns under circumflex, och så många eller som siffror i decimaldelen är de inte under circumflex.

Låt oss följa den här proceduren för att omvandla decimalnumret 0.428428428 ... i fraktion.

-Först identifieras perioden, som är den sekvens som upprepas: 428.

-Sedan görs driften av att subtrahera numret utan koma eller en accent: 0428 av den del som inte har någon circumflex, som är 0. Detta är 428 - 0 = 428.

-Nämnaren är byggd och vet att det under circumflex finns 3 siffror och alla är under circumflex. Därför är nämnaren 999.

-Slutligen bildas och förenklas fraktionen om möjligt:

0.428 = 428/999

Det är inte möjligt att förenkla mer.

Rationella nummeroperationer

- Lägga till och subtrahera

Bråk med samma nämnaren

När fraktionerna har samma nämnar, lägg till dem och/eller subtrahera dem är mycket enkelt, eftersom tellerna helt enkelt läggs till algebraiskt och lämnar som nämnaren av resultatet till samma av tilläggen. Slutligen, om möjligt, förenklas det.

Exempel

Utföra följande algebraiska summa och förenkla resultatet:

Den resulterande fraktionen är redan oreducerbar.

Bråk med olika nämnar

I detta fall ersätts adlarna av ekvivalenta fraktioner med samma nämnare och sedan beskrivs proceduren redan. 

Exempel

Algebraiskt lägg till följande rationella siffror förenkla resultatet:

Kan tjäna dig: kanter på en kub

Stegen är:

-Bestäm minsta vanliga multipel (MCM) för nämnaren 5, 8 och 3:

MCM (5,8,3) = 120

Detta kommer att vara nämnaren för den resulterande fraktionen utan att förenkla.

-För varje fraktion: Dela MCM mellan nämnaren och multiplicera med telleren. Resultatet av denna operation placeras, med dess respektive tecken, i fraktionens teller. På detta sätt erhålls en bråkdel som motsvarar originalet, men med MCM som nämnare.

Till exempel, för den första fraktionen, är telleren byggd så här: (120/5) x 4 = 96 och erhålls:

Fortsätt på samma sätt för de återstående fraktionerna:

Slutligen ersätts de motsvarande fraktionerna utan att glömma deras tecken och den algebraiska summan av tellerna görs:

(4/5) + (14/8) - (11/3) + 2 = (96/120) + (210/120) - (440/120) + (240/120) =

= (96+210-440+24) / 120 = -110 / 120 = -11/12

- Multiplikation och uppdelning

Multiplikation och uppdelning görs enligt reglerna som visas nedan:

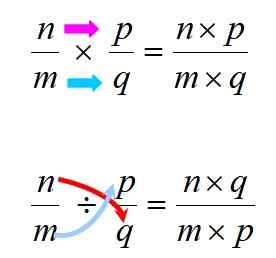Figur 3. Regler för att utföra multiplikation och uppdelning av rationella siffror. Källa: f. Zapata.

I alla fall är det viktigt att komma ihåg att multiplikation är kommutativ, vilket innebär att ordningen på faktorerna inte förändrar produkten. Detta händer inte med divisionen, så du måste se till att respektera ordningen mellan utdelning och divisor.

Exempel 1

Utföra följande operationer och förenkla resultatet:

a) (5/3) x (8/15)

b) (-4/5) ÷ (2/9)

Svara på

(5/3) x (8/15) = (5 x 8)/(3 x 15) = 15/120 = 1/8

Svar B

(-4/5) ÷ (2/9) = (-4 x 9)/(5 x 2) = -36/10 = -18/5

Exempel 2     

Luisa hade $ 45. Han tillbringade en tiondel med att köpa en bok och 2/5 delar av det som var kvar i en skjorta. Hur mycket pengar har Luisa kvar? Uttrycka resultatet i oåterkallelig fraktion.

Lösning

Bokkostnaden (1/10) x 45 $ = 0.1 x 45 $ = 4.5 $

Därför stannade Luisa hos:

45 - 4.5 $ = 40.5 $

Med de pengarna gick Luisa till klädaffären och köpte skjortan, vars pris är:

(2/5) x 40.5 $ = 16.2 $

Nu har Luisa i portföljen:

40.5 - 16.2 $ = 24.3 $

För att uttrycka det i fraktion är det skrivet så här:

24.3 = 243/10

Det är oåterkalleligt.

Referenser

1. Baldor, a. 1986. Aritmetisk. Codex -utgåvor och distributioner.
2. Carena, m. 2019. Matematikmanual. National University of the Coast.
3. Figuera, J. 2000. Matematik 8. Co-bo-utgåvor.
4. Jiménez, r. 2008. Algebra. Prentice hall.
5. Rationella nummer. Återhämtat sig från: Cimanet.Uoc.Edu.
6. Rationella nummer. Hämtad från: Webdelprofesor.Ula.gå.