Ortoedroformler, område, volym, diagonal, exempel

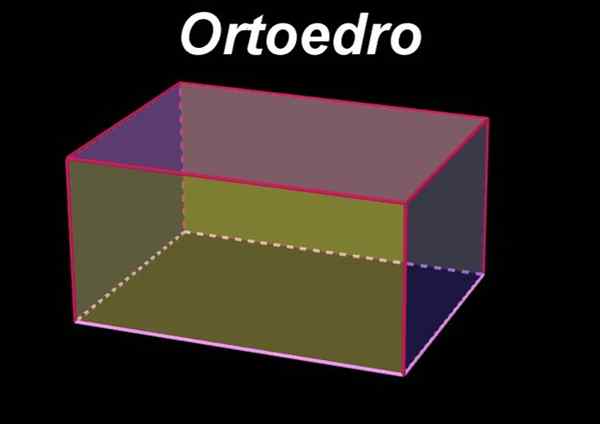
han Ortoedro Det är en volymetrisk eller tre dimensionell geometrisk figur som kännetecknas av att ha sex rektangulära ansikten, så att motsatta ansikten är i parallella plan och är identiska eller kongruenta rektanglar med varandra. Å andra sidan är ansikten intill ett givet ansikte i plan vinkelrätt mot det för det initiala ansiktet.

Det kan också övervägas när Ortoedro som ett ortogonalt rektangulärt basprismat, där dihedros vinklar De bildas av de två sidor planerna intill en gemensam kant, de mäter 90º. Den dihedrala vinkeln mellan två ansikten mäts vid skärningspunkten mellan ansikten med ett vinkelrätt och vanligt plan för dem.

Figur 1. Ortoedro. Källa: f. Zapata med geogebra.

På samma sätt är ortoedro en rektangel parallellpiped, Eftersom detta definieras till parallellepiped som den volymetriska figuren av sex ansikten, som är parallella två till två.

I alla parallellpipade är ansikten parallellogram, men i rektangeln måste parallellen ansikten vara rektangulära.

[TOC]

Delar av ortoedro

Delarna av en polyhedron, till exempel ortoedro, är:

-Kanter

-Häckar 

-Inslag

Vinkeln mellan två kanter på ett yta på ortoedro sammanfaller med den dihedrala vinkeln som bildas av dess andra två ansikten intill var och en av kanterna och bildar rätt vinkel. Följande bild klargör varje koncept:

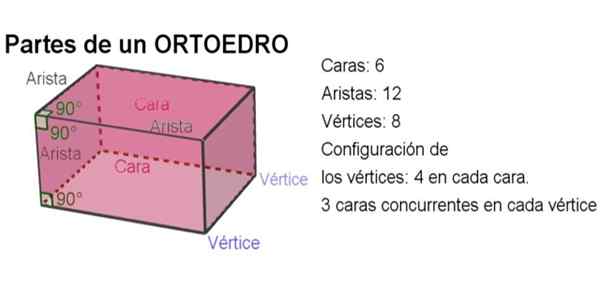figur 2. Delar av en ortoedro. Källa: f. Zapata med geogebra.

-Totalt har en ortoedro 6 ansikten, 12 kanter och 8 vertikaler.

-Vinkeln mellan två kanter är en rätt vinkel.

-Den dihedrala vinkeln mellan två sidor är också rak.

-I varje ansikte finns det fyra vertikaler och i varje toppunkt deltar tre ömsesidigt ortogonala ansikten.

Kan tjäna dig: vad är ett capicúa -nummer? Egenskaper och exempel

Ortoedroformler

Område

Ytan eller området på en Ortoedro Det är summan av områdena i deras ansikten.

Om de tre kanterna som instämmer i ett toppunkt har mått A, B och C, som visas i figur 3, har framsidan ett område C⋅b Och bakgrundsytan har också ett C⋅B -område.

Sedan har de två sidoytorna ett område A⋅b varje. Och slutligen har ansikten på golvet och taket området A⋅c varje.

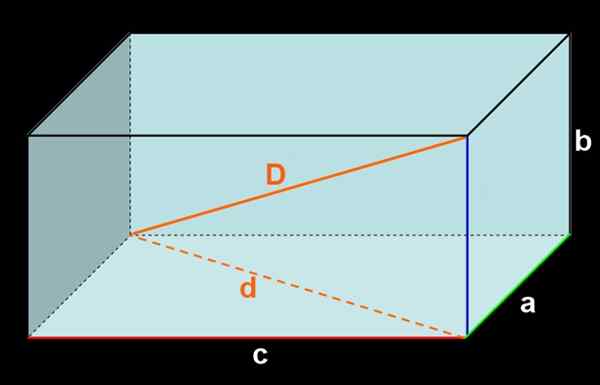Figur 3. Ortoedro av dimensioner a, b, c. Inre diagonal D och extern diagonal D.

Att lägga till området för alla ansikten erhålls:

A = 2⋅C⋅B + 2⋅AuldB + 2⋅A

Rita gemensam faktor och beställa villkoren:

A = 2⋅ (A⋅B + B⋅C + C⋅A)

Volym

Om ortoedro betraktas som ett prisma, beräknas dess volym enligt följande:

Volym = Prism Base Area X Höjden på prisma

I det här fallet tas dimensionsgolvet som ett rektangulärt c och till, Så basområdet är C'a.

Höjden ges av längden b Från de ortogonala kanterna till sidorna till och c.

Multiplicera basområdet (A⋅c) efter höjd b Du har volymen V Från ortoedro:

V = a⋅b⋅c

Inre diagonal

I en ortoedro finns det två typer av diagonaler: externa diagonaler och inre diagonaler.

De yttre diagonalerna är på rektangulära ansikten, medan de inre diagonalerna är de segment som går med två motsatta vertikaler, som förstås av motsatta vertikaler de som inte delar någon kant.

I en ortoedro finns det fyra inre diagonaler, alla lika mått. Längden på de inre diagonalerna kan erhållas från att applicera Pythagoras teorem för rektanglar.

Det kan tjäna dig: trigonometriska funktioner: grundläggande, i det kartesiska planet, exempel, träning

Längden D för den yttre diagonalen i ortoedrogolvet uppfyller Pythagorean -förhållandet:

d² = a² + c²

På liknande sätt är den inre mätningsdiagonalen i den pytagoriska förhållandet:

D² = D² + b².

Kombinera de två tidigare uttryck du har:

D² = a² + c² + b².

Slutligen ges längden på någon av de inre diagonalerna i ortoedro av följande formel:

D = √ (a² + b² + c² ). 

Exempel

- Exempel 1

En murare bygger en ortoedroformad tank vars inre dimensioner är: 6 m x 4 m bas och 2 m hög. Det begärs:

a) Bestäm tankens inre yta om den är helt öppen i sin övre del. 

b) Beräkna volymen på det inre utrymmet i tanken.

c) Hitta längden på en inre diagonal.

d) Vad är tankens kapacitet i liter?

Lösning till

Vi tar dimensionerna på den rektangulära basen a = 4 m och c = 6 m och höjden som b = 2 m

Området för en ortoedro med de givna dimensionerna ges av följande förhållande:

A = 2⋅ (A⋅B + B⋅C + C⋅A) = 2⋅ (4 M⋅2 M + 2 M⋅6 M + 6 M⋅4 M)

Det vill säga:

A = 2⋅ (8 m² + 12 m² + 24 m²) = 2⋅ (44 m²) = 88 m²

Det föregående resultatet är området för ortoedro stängt med de givna dimensionerna, men eftersom det är en tank som helt upptäcktes i sin övre del, för att få ytan på innerväggarna i tanken, området för det saknade locket det är:

C⋅A = 6 m ⋅ 4 m = 24 m².

Slutligen kommer tankens inre yta att vara: s = 88 m² - 24 m² = 64 m².

Lösning B

Tankens inre volym ges av volymen av en ortoedro i tankens inre dimensioner:

V = a⋅b⋅c = 4 m ⋅ 2 m ⋅ 6 m = 48 m³.

Lösning C

Den inre diagonalen i en oktaedron med dimensionerna på det inre av tanken har en längd som ges av:

Kan tjäna dig: kontinuerlig slumpmässig variabel

√ (a² + b² + c² ) = √ ((4 m)² + (2 m)² + (6 m)² )

Utföra de angivna operationerna vi har:

D = √ (16 m² + 4 m² + 36 m² ) = √ (56 m²) = 2√ (14) m = 7,48 m.

Lösning D

För att beräkna tankkapaciteten i liter är det nödvändigt att veta att volymen på en kubisk decimeter motsvarar en liter kapacitet. Det hade tidigare beräknats i volym i kubikmeter, men det måste omvandlas till kubiska decimeter och sedan till liter:

V = 48 m³ = 48 (10 dm)³ = 4.800 dm³ = 4.800 L

- Övning 2

Ett glasakvarium har en kubisk form på 25 cm sida. Bestäm området i M², Volymen i liter och längden på en inre diagonal i CM.

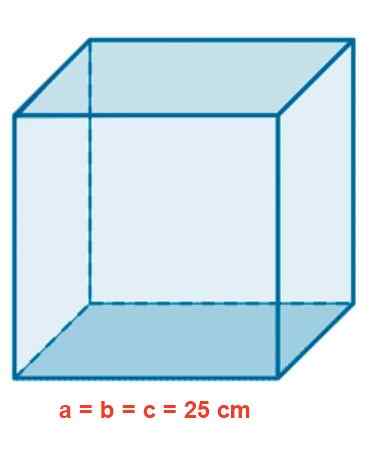Figur 4. Kubikglasakvarium.

Lösning

Området beräknas med samma ortoedroformel, men med hänsyn till att alla dimensioner är identiska:

A = 2⋅ (3 a⋅a) = 6⋅ a² = 6⋅ (25 cm)² = 1.250 cm²

Kubens volym ges av:

V = a³ = (25 cm)³ = 15.625 cm³ = 15.625 (0,1 dm)³ = 15 625 DM³ = 15,625 l.

Längden D för det inre diagonalen är:

D = √ (3: e²) = 25√ (3) cm = 43,30 cm.

Referenser

1. Arias j. Geogebra: Prism. Återhämtat sig från: YouTube.com.
2. Beräkning.Likström. Övningar och problem som lösts i områden och volymer. Återhämtad från: beräkning.Likström.
3. Salvador r. Pyramid + ortoedro med geogebra (IHM). Återhämtat sig från: YouTube.com
4. Weisstein, Eric. "Ortoedro". Matematik. Wolfram Research.
5. Wikipedia. Ortoedro. Återhämtad från: är.Wikipedia.com