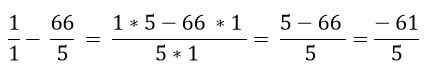Papomudor

Vad är Papomudas?

han Papomudor Det är ett förfarande för att lösa algebraiska uttryck. Dess förkortning indikerar ordern för prioritering av operationer: parenteser, krafter, multiplikation, uppdelning, tillägg och subtraktion. Med detta ord kan du enkelt komma ihåg i vilken ordning ett uttryck som består av flera operationer måste lösas.

Generellt sett kan du i numeriska uttryck hitta flera aritmetiska operationer tillsammans, såsom summor, subtraktion, multiplikationer och divisioner, som också kan vara fraktioner, krafter och rötter. För att lösa dem är det nödvändigt att följa en procedur som garanterar att resultaten kommer att vara korrekta.

Ett aritmetiskt uttryck som består av en kombination av dessa operationer måste lösas enligt ordningen, även känd som hierarkin för operationer, etablerad för länge sedan i universella konventioner. Således kan alla människor följa samma procedur och få samma resultat.

Egenskaper

Papomudas är en standardförfarande som fastställer den ordning som måste följas när ett uttryck måste ges, vilket består av en kombination av operationer som subtraktionssumma, multiplikation och uppdelning.

Denna procedur fastställer ordningen för prioritering av en operation i förhållande till de andra när de kommer att vara; det vill säga varje operation har en hierarkisk förändring eller nivå som ska lösas.

Ordningen i vilken de olika operationerna för ett uttryck måste lösas ges av varje förkortning av ordet Papomudas. På detta sätt måste du:

1. PA: Parenteser, fyrkantiga parenteser eller nycklar.
2. PO: krafter och rötter.
3. MU: Multiplikationer.
4. D: Divisioner.
5. A: Tillägg eller summor.
6. S: subtraktioner eller subtraktion.

Denna procedur kallas också på engelska som Pemdas; För att enkelt komma ihåg är detta ord associerat med frasen: "Ursäkta min kära moster Sally”, Där varje första bokstav motsvarar en aritmetisk operation, på samma sätt som Papomudas.

Hur man löser dem?

Baserat på hierarkin som upprättats av Papomudas för att lösa verksamheten för ett uttryck är det nödvändigt att uppfylla följande ordning:

• För det första måste alla operationer som är inom gruppsymboler, såsom parentes, nycklar, konsoler och fraktionsstänger lösas. När det finns grupperingssymboler inom andra bör du börja beräkna inifrån.

Kan tjäna dig: Kvadratiska successioner: Exempel, regel och övningar löst

Dessa symboler används för att ändra ordningen i vilken operationer löses, eftersom det som alltid finns inom dessa måste alltid lösas.

• Då löses krafterna och rötterna.
• På tredje plats löses multiplikationer och divisioner. Dessa har samma prioriteringsordning; Därför, när dessa två operationer finns i ett uttryck, måste den som verkar först lösas och läsa uttrycket från vänster till höger.
• I slutändan löses summorna och subtraktionen, som också har samma prioriteringsordning och därför löses det som visas först i uttrycket, läsning från vänster till höger.
• Verksamheten ska aldrig blandas när du läser från vänster till höger, du måste alltid följa ordningen om prioritet eller hierarki som upprättats av Papomudas.

Det är viktigt att komma ihåg att resultatet av varje operation måste placeras i samma ordning i förhållande till andra, och alla mellansteg måste separeras med ett tecken tills det når slutresultatet.

Ansökan

Papomudas procedur används när du har en kombination av olika operationer. Med hänsyn till hur de löses kan detta tillämpas i:

Uttryck som innehåller summor och subtraktioner

Det är en av de enklaste operationerna, eftersom båda har samma prioriteringsordning, så att den måste lösas från vänster till höger i uttrycket; Till exempel:

22 -15 + 8 +6 = 21.

Uttryck som innehåller summor, subtraktion och multiplikationer

I detta fall är den högsta prioriterade operationen multiplikation, sedan löses summorna och subtraktionen (den som är först i uttrycket). Till exempel:

6 _* 4 - 10 + 8 _* 6 - 16 + 10 _* 6

= 24 -10 + 48 - 16 + 60

= 106.

Uttryck som innehåller summan, multiplikation och uppdelning av subtraktion

I detta fall finns det en kombination av alla operationer. Det börjar med att lösa multiplikation och uppdelning som har överlägsen prioritet, sedan summorna och subtraktionen. När man läser uttrycket från vänster till höger löses det enligt dess hierarki och position inom uttrycket; Till exempel:

Kan tjäna dig: mumm

7 + 10 _* 13 - 8 + 40 ÷ 2

= 7 + 130 - 8 + 20

= 149.

Uttryck som innehåller summa, subtraktion, multiplikation, uppdelning och krafter

I detta fall höjs ett av siffrorna till en kraft, som inom prioritetsnivån måste lösas först och sedan lösa multiplikationer och divisioner och slutligen summorna och subtraktionen:

4 + 4² _* 12 - 5 + 90 ÷ 3

= 4 + 16 _* 12 - 5 + 90 ÷ 3

= 4 + 192 - 5 + 30

= 221.

Liksom krafterna har rötterna också den andra prioriteringsordningen; I uttryck som innehåller dem måste de därför först lösas än multiplikationer, divisioner, summor och subtraktion:

5 _* 8 + 20 ÷ √16

= 5 _* 8 + 20 ÷ 4

= 40 + 5

= 45.

Uttryck som använder gruppsymboler

När skyltar används såsom parenteser, nycklar, parenteser och fraktioner, som är inom dessa löses först, oavsett ordning om prioritering av den verksamhet som den innehåller i förhållande till de utanför detta, som om det kommer att hantera en separat uttryck:

14 ÷ 2 - (8 - 5)

= 14 ÷ 2 - 3

= 7 - 3

= 4.

Om det finns flera operationer måste dessa lösas genom hierarkisk ordning. Sedan löses de andra operationerna som utgör uttrycket; Till exempel:

2 + 9 * (5 + 2³ - 24 ÷ 6) - 1

= 2 + 9 * (5 + 8 - 4) - 1

= 2 + 9 * 9 - 1

= 2 + 81 - 1

= 82.

I vissa uttryck används grupperingssymboler inom andra, till exempel när det är nödvändigt att ändra tecknet på en operation. I dessa fall måste det börja med att lösa inifrån och ut; det vill säga, förenkla gruppsymbolerna som är i mitten av ett uttryck.

Generellt sett är beställningen att lösa operationer som finns i dessa symboler: Lös först vad som finns inom parentes (), sedan parentes [] och slutligen nycklarna .

90 - 3_*[12 + (5_*4) - (4_*2)]

= 90 - 3_* [12 + 20 - 8]

Kan tjäna dig: Teoretisk sannolikhet: Hur man får ut det, exempel, övningar

= 90 - 3 _* 24

= 90 - 72

= 18.

Övningar

Första träning

Hitta värdet på följande uttryck:

tjugo² + √225 - 155 + 130.

Lösning

Genom att tillämpa papomudorna måste krafterna och rötterna lösas först och sedan lägger till och subtraktion. I det här fallet tillhör de två första operationerna samma ordning, så den som är först löses, från vänster till höger:

tjugo² + √225 - 155 + 130

= 400 + 15 -155 + 130.

Lägg sedan till och subtraktion, börja till vänster också:

400 + 15 -155 + 130

= 390.

Andra träning

Hitta värdet på följande uttryck:

[- (6³ - 3⁶) ÷ (8 _* 6 ÷ 16)].

Lösning

Det börjar med att lösa de operationer som ligger inom parentesen, efter den hierarkiska ordningen som de har enligt Papomudas.

Först löses krafterna i den första parentesen, sedan löses operationerna för den andra parentesen. När de tillhör samma ordning löses den första operationen av uttrycket:

[- (6³ - 3⁶) ÷ (8 _* 6 ÷ 16)]

= [- (216- 729) ÷ (8 _* 6 ÷ 16)]

= [ - (216 - 729) ÷ (48 ÷ 16)]

= [- (-513) ÷ (3)].

Eftersom verksamheten inom parentes redan har lösts fortsätter nu den uppdelning som har den största hierarkin:

[- (-513) ÷ (3)] = [- (-171)]]].

Slutligen indikerar parentesen som skiljer minus (-) -tecknet från resultatet, som i detta fall är negativt, att en multiplikation av dessa tecken måste göras. Således är resultatet av uttrycket:

[- (-171)] = 171.

Tredje träning

Hitta värdet på följande uttryck:

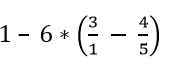
Lösning

Fraktioner som ligger inom parentesen löses:

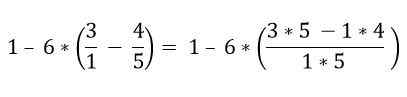
Inom parentesen finns det flera operationer. Multiplikationerna löses först och sedan subtraktionerna; I detta fall betraktas fraktionsstången som en gruppsymbol och inte som en uppdelning, så operationerna för den övre och nedre delen måste lösas:

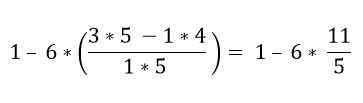
Genom hierarkisk ordning måste multiplikation lösas:

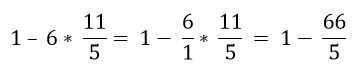
Slutligen löses subtraktionen: