Pascalina eller Pascal Machine

Vi förklarar vad Pascalina, dess historia, egenskaper och funktion är

Pascal de Pascal (1652). Källa: Rama, CC BY-SA 3.0 fr, via Wikimedia Commons

Vad är Pascalina?

De Pascalina Det är en mekanisk kalkylator, skapad av den franska forskaren och filosofen Blaise Pascal (1623-1661), omkring 1642, med bara 19 års ålder. Namnet "Pascalina" gavs till hans ära, även om det också kallades "Aritmetic Machine".

Tack vare ett växelsystem gjord av järn och noggrant artikulerat kan Pascalina lägga till och subtrahera, vilket är föregångaren till nuvarande kalkylatorer. Och precis som dessa har Pascalina ett gränssnitt för inträde av data som istället för nycklar använder en serie numrerade roterande skivor för att indikera positionsvärdet för varje siffra: enheter, tiotals, hundratals och mer.

De numrerade skivorna är försedda med hål, där en stav eller stilett införs för att vända dem genom steg.

Den inre mekanismen består av en serie delikat kopplade tandhjul, som rör sig, steg för steg, cylindrar med två spel från 0 till 9. Vissa fönster som finns på skivorna, tillåter att observera de värden som dessa siffror förvärvar, när du genomför en underlag eller subtraktionsoperation.

Historia

Sedan hans barndom hade Pascal redan visat sina stora intellektuella färdigheter, så hans far, magistrat och matematiker Etienne Pascal beslutade att ge honom bästa möjliga utbildning. 1642 skickades Etienne Pascal för att höja skatter i Rouen, Normandie, norr om Frankrike, ett verk som inte var lätt.

Blaise Pascal, fast besluten att hjälpa sin far, designade och byggde en maskin som, med mekaniska växlar, kunde rotera några hjul för att utföra och visa operationer av summor och subtraktion. Den här enheten kallades "Pascalina".

Blaise Pascal

Med Pascalina kan multiplikationer och divisioner också genomföras, men inte direkt, men genom successiva summor och subtraktion.

Kan tjäna dig: sidereal eller sidereh dag

Kostnaden för att tillverka Pascalina var emellertid mycket hög, så uppfinningen gick obemärkt av majoriteten vid den tiden. De som hade råd med en, föredrog att lämna den hemma och inte använda den för rutinmässigt arbete, så nästan alla fortsatte att lösa sin verksamhet på traditionellt sätt.

Mekanismen för Pascalina bör vara mycket exakt, så att kalkylatorn fungerade korrekt, men ofta slutade fungera. Och Pascal var den enda som kunde reparera det varje gång detta hände.

Pascal fortsatte att förbättra sin design under de kommande tio åren och nådde cirka 50 pascalinas, varav två bevaras: en är i Tyskland, i Zwinger -museet, i Dresde, Tyskland och en annan i Musée des Arts et Métiers, i Paris.

Egenskaper och funktion av Pascalina

Pascalina har egenskaper som är gemensamma för dagens kalkylatorer, som anges i början. Den uppenbara skillnaden är att Pascalina arbetar med mekaniska element, vars justering måste vara perfekt, medan dagens kalkylatorer arbetar med elektronik.

I grund och botten har Pascalina:

• Ett gränssnitt för att ange data, bestående av rattar som drivs av en stiletto.
• Den interna mekanismen som används för att bearbeta dessa data, baserat på växlar och mobila dentor.
• En panel som visar resultaten, med registreringsfönster, för att uppskatta rörelsen som introducerats i ratten och observera resultaten.

Summorna utförs direkt och flyttar ratten för att introducera varje siffra för tilläggen. Subtraktion görs emellertid inte direkt, men på ett sätt som i princip är ganska nyfiken: Pascalino -komplementet, vilket förklaras nedan:

Komplement till 9 eller Pascalino -komplement

Komplement till 9 är en numerisk teknik som omvandlar subtraktioner till summor, lättare att lösa med det mekaniska systemet implementerat av Pascal.

Kan tjäna dig: flödesdiagram

Om du till exempel vill lösa drift A - B lägger den till "A" med Pascalino -komplementet av "B", och resultatet av denna operation är den sökta subtraktionen.

Först förklaras hur man hittar komplementet till 9 av valfritt nummer N. Det är väldigt enkelt, det subtraheras från 9 varje siffra med det numret, som visas i följande exempel:

• Låt n = 20, dess komplement till 9 gör: 99 - 20 = 79
• För n = 347 måste du göra: 999 -347 = 652
• Om n = 7 är dess komplement till 9 2.

Subtraktioner genom komplement till 9

Anta nu att du vill utföra följande operation:

1246 - 822

Följande steg följs:

Steg 1: Hitta komplementet till 9 av de stulna, som är 822, som är 999 - 822 = 177.

Steg 2: Genomföra summan av minuend och komplementet till 9 tidigare hittade: 1246 + 177 = 1423, observera väl till vänster i resultatet i resultatet.

Steg 3: Den begärda subtraktionsoperationen är 423 + 1 = 424.

Läsaren kan kontrollera resultatet med en gemensam kalkylator!

Om minuendet är mindre än att subtrahera, fortsätt, till exempel för att utföra:

267 - 592

Steg 1: Hitta komplementet till 9 i underavsnitt 592, som är 999 - 592 = 407.

Steg 2: Lägg till minuend och komplement till 9 av de stulna: 267 + 407 = 674.

Steg 3: Beräkna komplement till 9 av resultatet: 999 - 674 = 325

Steg 4: Lägg till det negativa tecknet i resultatet: -325 och detta är den begärda subtraktionen.

Vid första anblicken verkar det mer komplicerat att göra en subtraktion på detta sätt, men med det tånade hjulsystemet är det lättare.

Hur fungerar Pascalina?

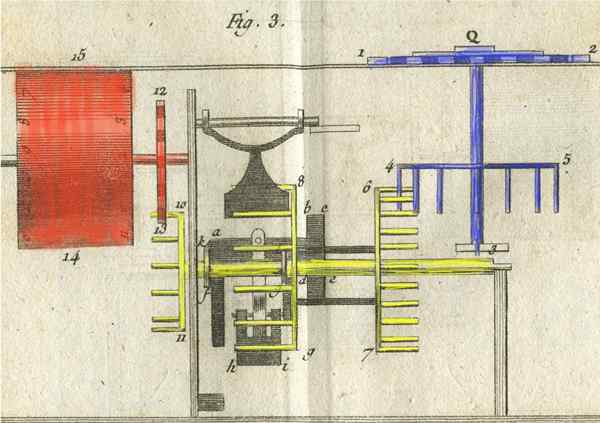
Inre mekanism för pascalina

Pascalina består i huvudsak av ett växelsystem som roterar 10 cylindrar som indikerar siffrorna. Varje cylinder samlar två serier av siffror, och varje serie går från 0 till 9.

Cylindern till den extrema höger indikerar enheterna, som följer dussintals, följande hundratals och så vidare. När en av cylindrarna kretsar en fullständig sväng gör mekanismen den till vänster framsteg. Ju fler siffror siffran har, desto fler hjul och cylindrar måste de flytta, vilket ger en uppfattning om den delikat av den inre mekanismen för Pascalina.

Kan tjäna dig: 11 exempel på fältforskning

Anmälan av siffrorna görs genom ratten numrerade utanför enheten, med en nål eller stilett, utformad för detta ändamål. Det finns rattar för enheter, tiotals, hundratals och mer, motsvarande var och en av cylindrarna.

Nu kommer du att se hur man genomför verksamheten.

Lägg till

Anta att du vill göra följande operation med en Pascalina:

25 + 14

Med alla initialiserade rattor i 0 rör sig TENS 2 -enheter eller steg, och enhetens urtavla rör sig i 5 steg. Med detta introduceras den första tillägget.

Sedan rör sig tennens 1 -enhet och enheterna till 4 till 4. Resultatet är: 39.

När en fullständig sväng tas till 8 och hjulen lägger till nödvändiga varv till de övre siffrorna, för att visa resultatet.

Subtrahera

För att subtrahera placeras alla ratten till 9, eftersom mekanismen påverkar subtraktionen genom komplement till 9, såsom anges i föregående avsnitt. Användaren behöver inte beräkna komplementet, mekanismen gör det i sig själv genom att initialisera DAL: erna med 9.

Till exempel vill du göra:

67 - 21

Det fortsätter på samma sätt som i summan, det vill säga tennens urtavla vrids i 6 steg och enheterna vänds i 7 steg. På detta sätt introduceras värdet på minuend. Sedan vrids ratten för TENS 2 steg och den av enheterna 1. Resultatet är 46, hur kan läsaren kontrollera.