Cirkelens omkrets Hur man får ut den och formler, lösta övningar

han cirkelens omkrets Det är uppsättningen punkter som bildar konturen i en cirkel och är också känd som längd av omkretsen. Det beror på radien, eftersom en större omkrets uppenbarligen kommer att ha en större kontur.

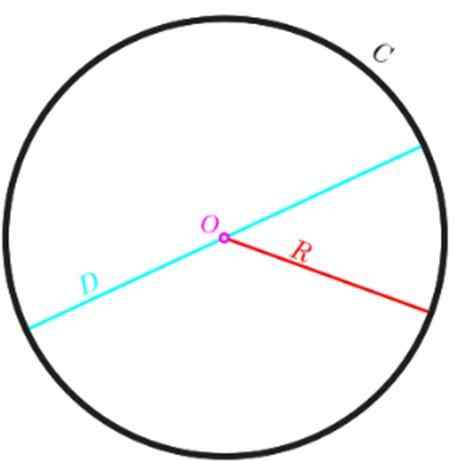
Vara P Omkretsen av en cirkel och R Radie för samma, då kan vi beräkna P Med följande ekvation:

P = 2π.R

Cirkelns omkrets (i detta fall en pizza) beror på sin radio. Källa: Pixabay.

Där π är ett riktigt nummer (läser "pi") som är värt cirka 3.1416 ... De suspensiva punkterna beror på att π har oändliga decimaler. Därför är det nödvändigt att avrunda dess värde när du gör beräkningarna.

Men för de flesta applikationer räcker det att ta det belopp som anges här, eller använda alla decimaler som räknaren som den fungerar.

Om det istället för att ha radien, föredras att använda diameter d, som vi vet är dubbelt radie, uttrycks omkretsen enligt följande:

P = π.2r = π.D

Eftersom omkretsen är en längd måste den alltid uttryckas i enheter som mätare, centimeter, fötter, tum och mer, beroende på systemet som föredras.

[TOC]

Omkretsar och cirklar

Det är ofta termer som används omväxlande, det vill säga som synonymer. Men det händer att det finns skillnader mellan dem.

Ordet "omkrets" kommer från den grekiska "perioden" som betyder kontur och "tunnelbana" eller mäter. Omkretsen är konturen eller omkretsen av cirkeln. Formellt definieras det:

En omkrets är uppsättningen punkter med lika avstånd till en punkt som kallas centrum, detta avstånd är omkretsens radie.

För sin del definieras cirkeln på följande sätt:

En cirkel är uppsättningen punkter vars avstånd till en punkt som kallas center är mindre än eller lika med ett fast avstånd som kallas radio.

Läsaren kan varna den subtila skillnaden mellan båda koncepten. Omkretsen hänvisar bara till uppsättningen av kantpunkter, medan cirkeln är uppsättningen punkter från kanten till insidan, av vilken omkretsen är gränsen.

Kan tjäna dig: Formel Clearance -övningar

Övningar av dEmoTration of the Circle Perimeter Calculation

Genom följande övningar kommer de beskrivna begreppen att genomföras, liksom vissa andra som kommer att förklaras som de visas. Vi börjar från den enklaste och svårighetsgraden kommer att ökas gradvis.

- Övning 1

Hitta omkretsen och området i 5 cm radiocirkeln.

Lösning

Ekvationen i början tillämpas direkt:

P = 2π.R= 2π.5 cm = 10 π cm = 31.416 cm

För att beräkna området TILL Följande formel används:

TILL = π.R² = π. (5 cm)²= 25π cm²= 78.534 cm²

- Övning 2

a) Hitta omkretsen och området i det tomma regionen i följande figur. Mitten av den skuggade cirkeln är vid den röda punkten, medan mitten av den vita omkretsen är den gröna punkten.

b) Upprepa föregående avsnitt för det skuggade regionen.

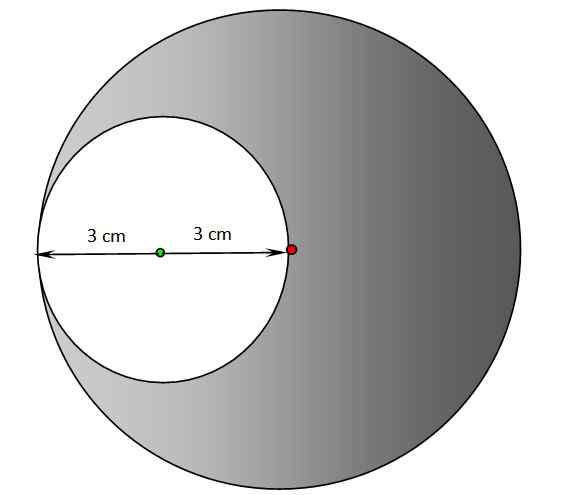Cirklar för övning 2. Källa: f. Zapata.

Lösning

a) Radien för den vita omkretsen är 3 cm, därför tillämpar vi samma ekvationer som i övning 1:

P = 2π.R= 2π.3 cm = 6 π cm = 18.85 cm

TILL = π.R² = π. (3 cm)²= 9π cm²= 28.27 cm²

b) För den skuggade cirkeln är radien 6 cm, dess omkrets är dubbelt så stor som beräknas i avsnitt A):

P = 2π.R= 2π.6 cm = 12 π cm = 37.70 cm

Och slutligen beräknas området i den skuggade regionen enligt följande:

- Först är området i den skuggade cirkeln som om den var klar, som vi kommer att kalla ', så här:

TILL' = π.R²= π.(6 cm)² = 36π cm²= 113.10 cm²

- Sedan till området TILL' Det vita cirkelområdet subtraheras, som tidigare beräknas i avsnitt A), på detta sätt erhålls det begärda området, vilket kommer att betecknas helt enkelt som:

A = a ' - 28.27 cm² = 113.10-28.27 cm² = 84.83 cm²

- Övning 3

Hitta området och omkretsen av det skuggade området i följande figur:

Kan tjäna dig: kompletterande vinklar: vad är, beräkning, exempel, övningar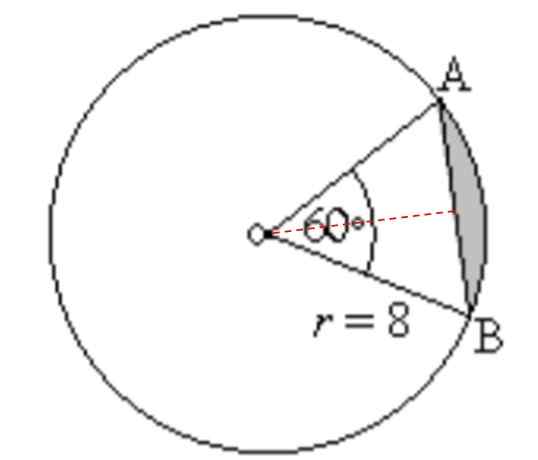Figur för övning 3. Källa: f. Zapata.

Lösning

Beräkning av området i det skuggade regionen

Vi beräknar först området för Cirkulär eller kil, mellan de raka segmenten OA och OB och det cirkulära AB -segmentet, som visas i följande figur:

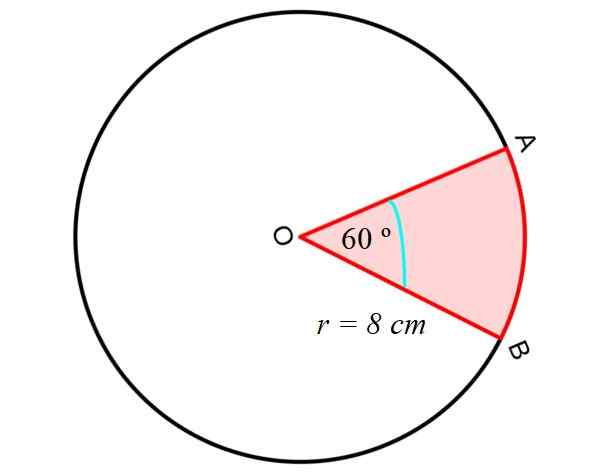
För detta används följande ekvation, vilket ger oss området för en cirkulär sektor, och känner till radien R och den centrala vinkeln mellan OA- och OB -segmenten, det vill säga två av omkretsens radioapparater:

TILL _Cirkulär = Π.R². (αº/360º)

Där aº är den centrala vinkeln - den är central eftersom dess toppunkt är mitten av omkretsen - mellan två radioapparater.

Steg 1: Beräkning av cirkulära sektorområdet

På detta sätt är sektorns område som visas i figuren:

TILL _Cirkulär = Π.R². (αº/360º) = π. (8 cm)². (60º/360º) = (64/6) π cm²= 33.51 cm²

Steg 2: Beräkning av triangelområdet

Då beräknar vi det vita triangeln i figur 3. Denna triangel är liksidig och dess område är:

TILL _triangel = (1/2) bas x höjd

Höjden är den prickade röda linjen som ses i figur 4. För att hitta det kan du till exempel använda Pythagoras -teoremet. Men det är inte det enda sättet.

Observatörsläsaren kommer att ha märkt att den liksidiga triangeln är uppdelad i två identiska rektanglar, vars bas är 4 cm:

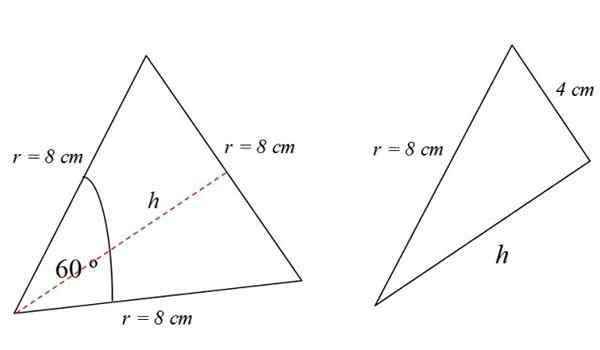
I en höger triangel uppfylls därför Pythagoras teorem: därför:

Eftersom du har höjden på triangeln, både rektangeln och det liksidiga, beräknas dess område:

TILL _triangel = (1/2) bas x höjd = (1/2) 8 cm x 6.93 cm = 27.71 cm².

Steg 3: Beräkning av det skuggade området

Det räcker för att subtrahera huvudområdet (det i den cirkulära sektorn) i det mindre området (det för den liksidiga triangeln): a _{skuggad region} = 33.51 cm² - 27.71 cm² = 5.80 cm².

Beräkning av omkretsen av det skuggade regionen

Den sökta omkretsen är summan av den 8 cm rektilinära sidan och AB -omkretsbågen.  Emellertid underkastar den fullständiga omkretsen 360 º, därför är en båge som under 60 º 60 º är en sjätte del av hela längden, som vi vet är 2.π.A:

Kan tjäna dig: Växande funktion: Hur man identifierar den, exempel, övningar

AB = 2.π.R / 6 = 2.π.8 cm / 6 = 8.38 cm

Ersätter, omkretsen av det skuggade regionen är:

P = 8 cm + 8.38 cm = 16.38 cm.

Ansökningar

Omkretsen, som området, är ett mycket viktigt koncept inom geometri och med många tillämpningar i det dagliga livet.

Konstnärer, designers, arkitekter, ingenjörer och många andra använder sig av omkretsen medan de utvecklar sitt arbete, särskilt en cirkel, eftersom den runda formen är överallt: från reklam, genom mat till maskiner.

Omkretsen och cirkeln är bland de mest använda geometrierna. Källa: Pixabay.

För att veta direkt längden på en cirkel räcker det att linda in den med en tråd eller sträng, sedan utöka den här tråden och mäta den med en bandband. Det andra alternativet är att mäta cirkelns radie eller diameter och använda några av de formler som beskrivs ovan.

I det dagliga arbetet används omkretsbegreppet när:

-Lämplig mögel väljs för en viss pizza eller kakestorlek.

-En urban väg kommer att designas genom att beräkna storleken på en redoma där bilar kan vända sig för att ändra mening.

-Vi vet att jorden kretsar kring solen i en ungefär cirkulär bana -i verkligheten är planetbanorna elliptiska, enligt Keplers lagar -men omkretsen är en mycket bra strategi för de flesta planeter.

-Den lämpliga storleken på en ring eller ring som kommer att köpas i en onlinebutik väljs.

-Vi väljer en nyckel till rätt storlek för att lossa en mutter.

Och många fler.

https: // youtu.Vara/cr8xjryl5tk

Referenser

1. Gratis matematikhandledning. Område och omkrets av en cirkel - geometri -kalkylator. Återhämtat sig från: Analyzemath.com.
2. Matematik öppen referens. Omkrets, omkrets av en cirkel. Återhämtat sig från: MathPenref.com.
3. Monterey Institute. Omkrets och område. Återhämtat sig från: MontereyInstitute.org.
4. Forskning. Hur man hittar en cirkels omkrets. Återhämtat sig från: forskning.com.
5. Wikipedia. Omkrets. Hämtad från: i.Wikipedia.org.