Manometrisk tryckförklaring, formler, ekvationer, exempel

De mättryck P_m Det är en som mäts i förhållande till ett referenstryck, som i de flesta fall väljs som atmosfärstrycket P_Bankomat vid havsnivån. Det är då a Relativ tryck, en annan term som det också är känt.

Det andra sättet på vilket trycket vanligtvis mäts jämför det med den absoluta tomheten, vars tryck alltid är noll. I det här fallet talas det om absolut tryck, som vi kommer att beteckna hur p_till.

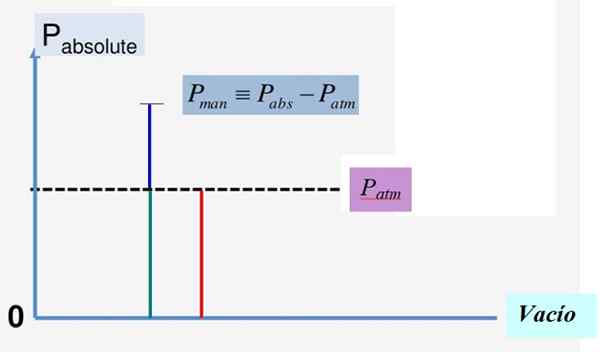
Figur 1. Absolut tryck och manometriskt tryck. Källa: f. Zapata.

Det matematiska förhållandet mellan dessa tre mängder är:

P_till = P_Bankomat + P_m

Därför:

P_m = P_till - P_Bankomat

Figur 1 illustrerar bekvämt detta förhållande. Eftersom vakuumtrycket är 0 är det absoluta trycket alltid positivt och detsamma gäller för atmosfärstryck P_Bankomat.

Manometriskt tryck används vanligtvis för att beteckna tryck ovanför atmosfärstrycket, såsom det som transporteras av däcken eller det i botten av havet eller en pool, som utövas av vikten av vattenkolonnen. I dessa fall s_m > 0, sedan s_till > P_Bankomat.

Det finns emellertid absoluta tryck under P_Bankomat. I dessa fall s_m < 0 y recibe el nombre de vakuumtryck Och det bör inte förväxlas med det redan beskrivna vakuumet, vilket är frånvaron av partiklar som kan utöva tryck.

[TOC]

Formler och ekvationer

Trycket i en vätska -vätska eller gas -är en av de mest signifikanta variablerna i sin studie. I en stationär vätska är trycket detsamma på alla pekar på samma djup oavsett orientering, medan rörelsen av vätskor i rören orsakas av tryckförändringar.

Medeltrycket definieras som kvoten mellan kraften vinkelrätt mot en yta F_⊥ och området för nämnda yta A, som uttrycks matematiskt på följande sätt:

P = f_⊥ /TILL

Trycket är en skalmängd, vars dimensioner är av kraft per yta. Enheterna i din åtgärd i International Units System (SI) är Newton/M², Kallas Pascal och förkortas som PA, till hedern för Blaise Pascal (1623-1662).

Multiplar som kilo (10³) och mega (10⁶) De används ofta, eftersom atmosfärstrycket vanligtvis är i intervallet 90.000 - 102.000 PA, vilket är lika med: 90 - 102 kPa. Trycket på ordningen av megapascalerna är inte sällsynta, så det är viktigt att bekanta sig med prefixen.

I Anglo -Saxon -enheter mäts trycket i pund/fot², Men det vanliga är att göra i pund/tum² antingen psi (Pundkraft per kvadrat tum).

Kan tjäna dig: Värmeöverföring: lagar, överföringsformulär, exempel

Variation av tryck med djup

Ju mer vi fördjupar oss i vattnet i en pool eller i havet, desto mer tryck upplever vi. Tvärtom, ökande höjd, atmosfärstrycket minskar.

Det genomsnittliga atmosfärstrycket vid havsnivån upprättas i 101300 PA eller 101.3 kPa, medan i Mariana -gropen i västra Stilla havet - det största djupet som är känt - är det cirka 1000 gånger högre och på toppen av Everest är bara 34 kPa.

Det är uppenbart att tryck och djup (eller höjd) är relaterade. Att veta i fallet med en viloplätare (statisk balans) anses det vara en vätskeparti med skivformad vätska, begränsad i en behållare, (se figur 2). Skivan har tvärsnitt TILL, vikt Dj och höjd Dy.

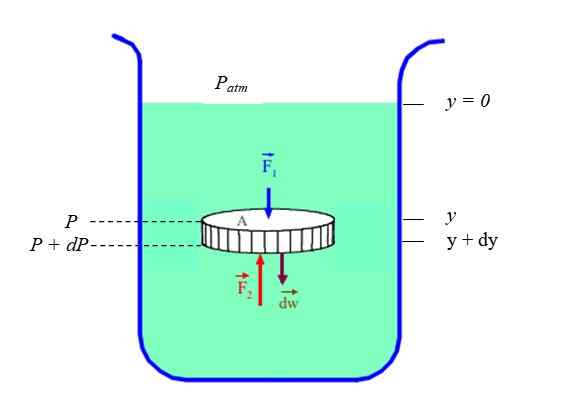figur 2. Differentiellt element i statisk jämviktsvätska. Källa: Fanny Zapata.

Vi ringer P vid trycket som finns i djupet "och"och P + dp vid trycket som finns i djupet (och + dy). Eftersom vätskans densitet ρ är orsaken mellan dess massa Dm och dess volym Dv, Du måste:

ρ = DM/ DV ⇒ DM = ρ.Dv

Därför vikten Dj av elementet är:

dw = g. DM = ρ.g.Dv

Och nu gäller Newtons andra lag:

Σ f_och = F₂ - F₁ - Dw = 0

(P + DP).A - p.TILL - ρ.g.Dv = 0

(P + DP).A - p.TILL - ρ.g. TILL. Dy = 0

Dp = ρ.g.Dy

Differentiell ekvationslösning 

Integrera båda sidor och med tanke på den tätheten ρ, liksom allvar g De är konstant, det finns det sökande uttrycket:

P₂ - P₁ = 5P = ρ.g.(och₂ - och₁)

ΔP = ρ.g. Δoch

Om det i det tidigare uttrycket väljs P₁ som atmosfärstryck och och₁ Som vätskans yta, då och₂ Det ligger på ett djup h och Δp = p₂ - P_Bankomat Det är det manometriska trycket beroende på djupet:

P_m = ρ.g.h

Om du behöver det absoluta tryckvärdet läggs atmosfärstrycket helt enkelt till föregående resultat.

Exempel

För manometriskt tryckmått används en enhet Tryckmätare, som i allmänhet erbjuder tryckskillnader. I slutändan kommer principen om drift av en U -delad tryckmanometer att beskrivas, men låt oss nu se några viktiga exempel och konsekvenser av den tidigare drygsatta ekvationen.

Pascal -principen

Ekvationen ΔP = ρ.g.(och₂ - och₁) Det kan skrivas som  P = po + ρ.g.h, var P är trycket på djupet h, medan P_antingen Det är trycket på vätskan, vanligtvis P_Bankomat.

Uppenbarligen varje gång du ökar Po, ökning P i samma mängd, så länge det är en vätska vars densitet är konstant. Det är just vad som skulle överväga ρ konstant och placera den utanför det integrerade löst i föregående avsnitt.

Kan tjäna dig: enkel harmonisk rörelse

Pascal -principen säger att varje ökning av trycket på en vätska som är begränsad i jämvikt, överförs utan någon variation till alla punkter av nämnda vätska. Genom den här egenskapen är det möjligt att multiplicera tvinga F₁ appliceras på vänster vänster vänster F₂ till höger.

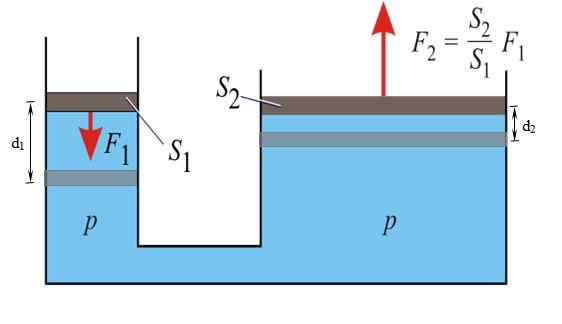Figur 3. I den hydrauliska pressen tillämpas Pascal -principen. Källa: Wikimedia Commons.

Bilbromsar fungerar under denna princip: En relativt liten kraft appliceras på pedalen, som blir en viktig kraft på bromscylindern på varje hjul, tack vare vätskan som används i systemet.

Stevins hydrostatiska paradox

Den hydrostatiska paradoxen säger att kraften på grund av trycket på en vätska längst ner på en behållare kan vara lika, större eller mindre än själva vätskans vikt. Men när du sätter behållaren ovanpå skalan kommer den normalt att registrera vätskans vikt (plus den av behållaren naturligtvis). Hur man förklarar denna paradox?

Vi börjar från det faktum att trycket längst ner i behållaren uteslutande beror på djupet och är oberoende av formen, som härleds i föregående avsnitt.

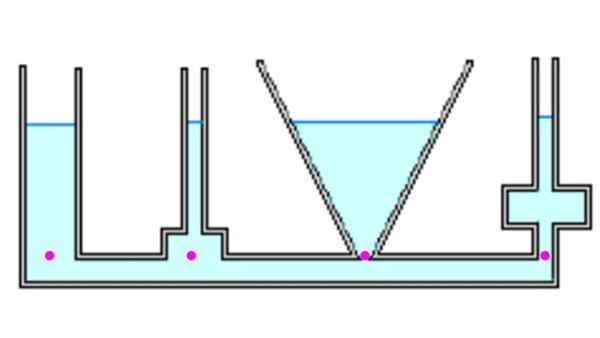Figur 4. Vätskan når samma höjd i alla behållare och trycket i bakgrunden är detsamma. Källa: f. Zapata.

Låt oss titta på några olika containrar. När de kommuniceras, när de är fyllda med vätska, når alla samma höjd h. De framträdande punkterna är vid samma tryck, eftersom de är på samma djup. Kraften på grund av trycket vid varje punkt kan dock skilja sig från vikten, (se exempel 1 nedan).

Övningar

Övning 1

Jämför kraften som utövas av trycket på botten av var och en av behållarna med vätskans vikt och förklara varför skillnaderna, om det finns några.

Behållare 1 

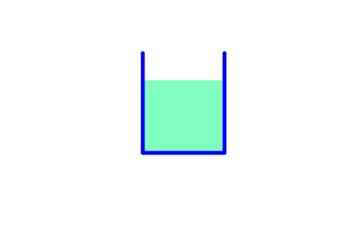Figur 5. Trycket i bakgrunden är detsamma i storleken till vätskans vikt. Källa: Fanny Zapata.

I denna behållare är basområdet därför:

Vätskevikt: mg = ρ.V.G = ρ . TILL .h . g

Tryck på botten: ρ. g. h

Kraft på grund av tryck: f = p.A = ρ. g. h. TILL

Vikten och kraften på grund av trycket är lika.

Container 2 

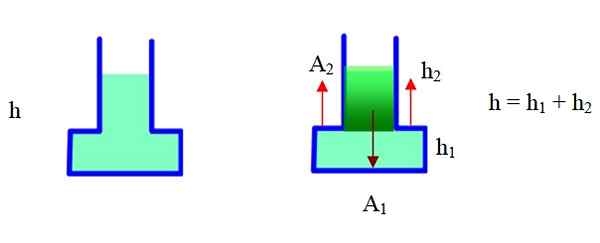Figur 6. Kraften på grund av trycket i denna behållare är större än vikten. Källa: f. Zapata.

Behållaren har en smal del och en bred del. I rätt schema har det delats upp i två delar och kommer att använda geometrien för att hitta den totala volymen. Området a₂ är extern till behållaren, h₂ Det är höjden på den smala delen, h₁ Det är höjden på den breda delen (basen).

Kan tjäna dig: Pleiades: historia, ursprung och komposition

Den kompletta volymen är volymen på basen + volymen på den smala delen. Med dessa data har du:

Vätskevikt: m . G = ρ . g. V = ρ . g. [TILL₁ .h₁+ (TILL₁ -TILL₂) .h₂] =

= ρ . g (a₁.ha₂h₂) = ρ . g . TILL₁.H - ρ . g . TILL._. h₂ (Användning av h = h₁ +h₂)

Tryck på botten: p = ρ. g. h

Kraft på botten på grund av tryck: f = p. TILL₁ = ρ. g. h. TILL₁

Jämförelse av vätskans vikt med kraften på grund av trycket som det noteras att detta är större än vikten.

Vad som händer är att vätskan också utövar styrka från steget i behållaren (se figurens röda pilar) som ingår i den föregående beräkningen. Denna motverkande kraft till de som utövas och vikten som registreras av skalan är resultatet av dessa. Enligt detta är storleken på vikten:

W = kraft på bakgrunden - styrka på den förskjutna delen = ρ . g . TILL₁.H - ρ . g . TILL._. h₂

Övning 2

Figuren visar en öppen rörtrycksmätare. Den består av ett U -rör, där en av ändarna är vid atmosfärstrycket och det andra ansluter till S, systemet vars tryck kommer att mätas.

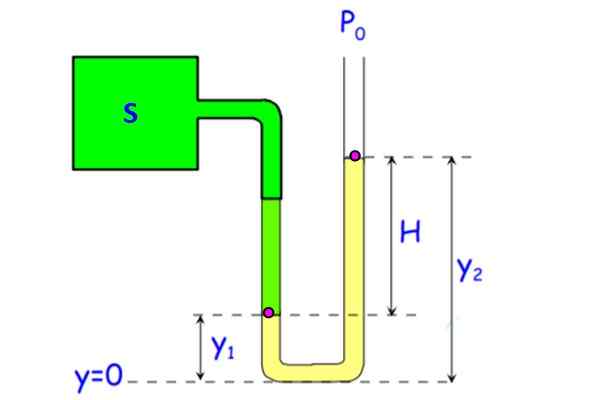Figur 7. Öppet rörtrycksmätare. Källa: f. Zapata.

Vätskan i röret (i gult i figuren) kan vara vatten, även om kvicksilver används för att minska enhetens storlek. (En skillnad på 1 atmosfär eller 101.3 kPa kräver en 10 vattenspelare.3 meter, inget bärbart).

Det uppmanas att hitta det manometriska trycket P_m I S -systemet, beroende på höjden H på vätskekolonnen.

Lösning

Trycket i bakgrunden för båda grenarna i röret är detsamma, för att vara i samma djup. Låt P_TILL Trycket vid punkt A, belägen i och₁ Och s_B de i punkt B som är på höjden och₂. Eftersom punkt B är belägen i vätskan och luftgränssnittet är trycket där P_antingen. I denna tryckmätningsgren är trycket längst ner:

PO + ρ.g.och₂

För sin del är trycket längst ner för vänster gren:

P + ρ.g.och₁

Där p är systemets absoluta tryck och ρ är vätskans densitet. Lika båda tryck:

PO + ρ.g.och₂ = P +ρ.g.och₁

Clearing P:

P = po + ρ.g.och₂ - ρ.g.och₁ = Po + ρ.g (och₂ - och₁) = Po + ρ.g. H

Därför manometriskt tryck P_m Det ges av P - p_antingen = ρ.g. H Och för att ha sitt värde räcker det för att mäta höjden som den manometriska vätskan stiger och multiplicerar den med värdet av g och vätsketäthet.

Referenser

1. Cimbala, c. 2006. Mekanik för vätskor, grundläggande faktorer och applikationer. Mc. Graw Hill. 66-74.
2. Figueroa, D. 2005. Serie: Physics for Science and Engineering. Volym 4. Vätskor och termodynamik. Redigerad av Douglas Figueroa (USB). 3-25.
3. Mott, r. 2006. Flytande mekanik. 4th. Utgåva. Pearson Education. 53-70.
4. Shaugnessy, E. 2005. Introduktion till vätskemekanik.Oxford University Press. 51 - 60.
5. Stylianos, V. 2016. Till enkel förklaring av den klassiska hydrostatiska paradoxen. Återhämtat sig från: Haimgaifman.Filer.WordPress.com