Relativ tryckformel, hur den beräknas, exempel, träning

De PresiRelativ Ón Det är vad som mäts med avseende på ett visst värde eller Utgångspunkt, vilket vanligtvis är atmosfärstryck vid havsnivån (standard atmosfärstryck). Detta är lämpligt eftersom en stor del av tryckmätningarna utförs under de gasformiga skikten som utgör atmosfären, som utövar sitt eget tryck.

Å andra sidan mäts det absoluta trycket med avseende på ett totalt vakuum, där det inte finns några molekyler som interagerar. I en behållare där vakuumet har gjorts finns det inga partiklar som verkar från insidan på väggarna eller på föremål inom den.

Figur 1. För att mäta det relativa trycket används en tryckmätare så här. Källa: Wikimedia Commons.

De uppmätta trycket kan vara över eller under atmosfärstrycket. I det första fallet talas det om mättryck Och i den andra av vakuumtryck.

Normalt är trycket som mäts dagligen i däcken och blodtrycket relativa tryck, medan när atmosfärstrycket mäts med en barometer är det ett absolut tryck.

[TOC]

Relativ tryckformel

Det relativa trycket är skillnaden mellan det absoluta trycket p_magmuskler och atmosfärstryck p_Bankomat, Det är ett differentiellt tryck eller skillnad i tryck. Vid det relativa trycket p_Rel Det är känt på engelska som Mättryck P_g Och det ges av förhållandet:

P_magmuskler = P_Bankomat + P_g

P_Rel = P_magmuskler - P_Bankomat

För tryck används Pascal som en måttenhet på det internationella enhetssystemet, oavsett om det är ett absolut tryck eller ett relativt tryck.

Pascal motsvarar kraften som utövas av 1 Newton över ett område på 1 m², Men andra enheter används ofta, såsom kvicksilver, vatten, anglo -saxon -enheter som psi och andra.

Kan tjäna dig: de 31 typerna av kraft i fysik och deras egenskaper

Hur beräknas det relativa trycket?

Om absolut tryck är känt vid en punkt och standard atmosfärstryck är det relativa trycket subtraktionen mellan båda.

Anta till exempel att det absoluta trycket i ett visst system är 305 kPa. Att veta att standard atmosfärstryck är 101.3 kPa, det relativa trycket är:

P_g = P_magmuskler - P_Bankomat = 305 - 101.3 kpa = 203.7 kpa

KPA eller kilopascal är tusen gånger större än en Pascal. Det används oftare, eftersom tryckvärden är i storleksordningen tusentals Pascal. Vikten på ett äpple är ungefär 1 Newton och en pascional motsvarar denna kraft som distribueras på en torg på 1 meter. Andra multiplar som Megapascal (1 MPa = 1 x 10⁶ Pa) eller Gigapascal (1 GPA = 1x 10⁹ Pa).

Exemplets tryck är manometriskt, eftersom det är över atmosfärstrycket, men det finns absoluta tryck under detta. Till exempel, om en gas i en behållare har ett absolut tryck på 50 kPa, är dess relativa tryck ett vakuumtryck som ger sug:

P_g = P_magmuskler - P_Bankomat = 50 - 101.3 kpa = -51.3 kpa

I dessa exempel användes det vanliga atmosfärstrycket, vilket är trycket vid havsnivån. Men om mer noggrannhet krävs i beräkningen kan lokalt atmosfärstryck användas, vilket kan skilja sig från 101.3 kPa, eftersom det beror på höjd och andra geografiska förhållanden.

I texterna är vanligtvis de tryck som ges relativa, och om det krävs att arbeta med absoluta tryck, skiljer dessa med användning av prenumerationer för att undvika förvirring.

Kan tjäna dig: sol

Variation av tryck med djup

Vid varje punkt inuti en vätska som vatten finns det tryck. Förutsatt att vattnet är inkomprimerbart, så att densiteten förblir konstant och trycket varierar vertikalt.

Det kan kontrolleras genom att ta en liten del av vätska i form av en tjock skiva Dy det är i vila mitt i flytande massa.

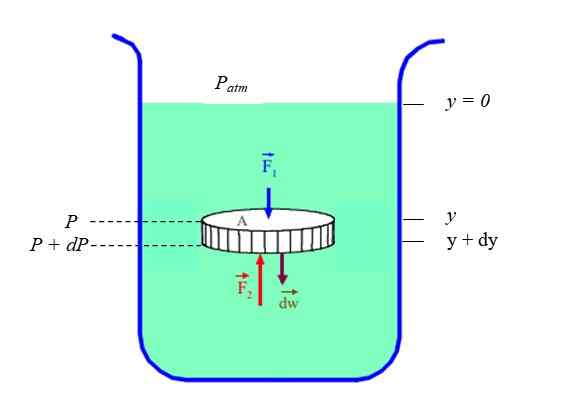figur 2. En liten del av diskformad vätska, i statisk jämvikt. Källa: f. Zapata.

Krafterna på skivans cirkulära kanter avbryts av kamrater, men inte de krafter som utövas av vätskemassan över och under skivan: F₁ och F₂. Dessutom är det nödvändigt att ta hänsyn till vätskeskivans viktW I Newtons andra lag:

∑f_och = F₂ - F₁ - W = 0

Dessa krafter kan uttryckas i termer av trycket, som är den vinkelräta kraften per areenhet. På detta sätt har vi trycket P, producerat med kraft F₁:

F₁ = P. TILL

Där a är skivans cirkulära område. Liknande:

F₂ = (P + dp). TILL

Med P + dp trycket på djupet och + dy. Vikten är dw = dm . G:

(P + DP). A - p. A - DM . G = 0

Vätsketätheten är ρ = DM/ DV, med DV vätskeskivans volym, som ges av a.Dy. Den här vägen:

(P + DP). A - p. A - ρa.Dy .G = 0

Ekvationen som erhålls förenklas för:

Dp - ρgdy = 0 → dp = ρgdy

Integrera båda sidor från och₁ upp till y₂:

= P₂ - P₁ = ρg (och₂ - och₁)

Termen p₂ - P₁ Det är en skillnad i tryck eller differentiellt tryck. Om vi ​​vill veta trycket vid den vertikala koordinatpunkten och gör vi det och₁ = 0, och₂ = y och P_antingen = P_Bankomat. Med detta kommer vi att ha trycket relativt detta djup, som enbart beror på djupet och:

Kan tjäna dig: oregelbunden galax: bildning, egenskaper, typer, exempel

P₂ - P_Bankomat = ρgy ⇒ P_Rel = ρgy

Exempel på relativt tryck

Tryck längst ner i en pool

Vi har alla upplevt det tryck som känns genom att fördjupa oss i en pool eller i havet. Vad är det relativa trycket som känns genom att vara nedsänkt i en sötvattenpool på 5 meter djup? Med det tidigare uttrycket och att veta att tätheten av färskt vatten är 1000 kg/m³, Med g = 9.81 m/s² Det relativa trycket är:

P_Rel = ρgy = 1000 x 9.81 x 5 Pa = 49050 PA.

Trycka på ett däck

Fordonsdäck är vanligtvis vid ett tryck på 32 psi. Detta är ett relativt eller manometriskt tryck i pund per kvadrat tum, enheten som används i engelska -talande länder. Många manometrar är kalibrerade i dessa enheter. 32 PSI är lika med 220632 PA O 220 KPA.

Träning löst

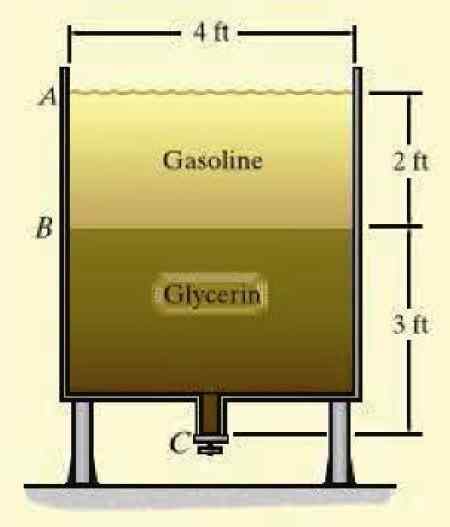
En tank innehåller bensin och glycerin, två icke -miskbara vätskor (blanda inte) i de angivna höjderna. Vad är det manometriska trycket längst ner i tanken? De specifika vikterna är fästa, betecknade med den grekiska bokstaven y, för varje vätska:

y_gas = 45.3 lb/ft³

y_Gly = 78.7 lb/ft³

Figur 3. En tank full med två icke -miscible vätskor. Källa: Hibbeler, R. Flytande mekanik.

Lösning

Den specifika vikten y för en vätska är produkten av dess densitet på grund av tyngdkraften, därför kan ekvationen för det relativa trycket uttryckas enligt följande:

P_Rel = γ.och

Det relativa trycket längst ner på tanken beror på både vikten på glycerinkolonnen och bensin och är oberoende av tankens form:

P_Rel = γ_gas . och_Ab + y_Gly . och_{före Kristus} = (45.3 x 2 + 78.7 x 3) lb/ft² = 326.7 lb/ft²

Referenser

1. Cimbala, c. 2006. Mekanik för vätskor, grundläggande faktorer och applikationer. Mc. Graw Hill.
2. Hibbeler, R. 2015. Flytande mekanik. Första. Ed. Pearson.
3. Mott, r.  2006. Flytande mekanik. 4th. Utgåva. Pearson Education.
4. Sitter, a. 2006. Flytande mekanik, en fysisk introduktion. Alfa -omega.
5. Gator, v. 1999. Flytande mekanik. McGraw Hill.
6. Zapata, f. Tryck och djup. Återhämtat sig från: FrancesPhysics.Bloggfläck.com.