Förklaring av första balansförhållandena, exempel, övningar

De Första balansförhållandet Det kräver att sumptorialvektorn för alla krafter som verkar på en kropp är ogiltig, så att den är i vila (statisk balans) eller med enhetlig rektilinär rörelse (dynamisk jämvikt).

Denna summa av krafter är ingen annan än nettokraften som verkar på kroppen och uttrycker detta läge matematiskt:

F_Netto = 0

∑ F = 0

Figur 1. Byggare av antiken har redan använt det första jämviktstillståndet, vilket framgår av Stonehenge -monumentet. Källa: Pixabay.

I rymden ger det första jämviktstillståndet upphov till tre ekvationer, en för varje dimension:

∑ f_x = 0; ∑ f_och = 0 och ∑ f_z = 0

När dessa ekvationer är nöjda rör sig objektet inte eller om det gör det kommer det att vara med konstant hastighet.

Observera runt oss inser vi att vi ständigt försöker uppfylla det första balansvillkoret så att saker inte faller.

Därför försöker den kompensera för jordens gravitation attraktion genom stöd, rep eller stöd av vissa, så att saker förblir på plats och inte går till marken.

Andra gånger är det som behövs för att förhindra externa elektromagnetiska fält från att störa driften av elektriska kretsar och kommunikationsenheter. I så fall är det de elektriska avgifterna som måste vara i balans.

[TOC]

Exempel

Ett stort antal vardagliga föremål uppfyller det första jämviktstillståndet, det handlar om att observera noggrant:

Byggnader

Byggare söker stabilitet i konstruktioner så att användare håller sig säkra. Syftet med statisk är att studera villkoren för statisk balans i byggnader, broar, vägar och alla slags strukturer.

Higaforer och hängande varningar

Dessa signalanordningar måste förbli fixerade för att uppfylla sina funktioner, därför är de föremål för kablar, stolpar och stavar på ett sådant sätt att det första balansvillkoret uppfylls.

Det kan tjäna dig: Tredje lagen om termodynamik: formler, ekvationer, exempelfigur 2. Trafikljus och hängande varningar utsätts på ett sådant sätt att det uppfyller det första jämviktstillståndet. Källa: PXFuel.

Elektrostbalansdrivrutinertakvåning

När ledande material som koppar och andra metaller förvärvar elektrisk laddning, etableras den elektrostatiska balansen inom kort, vilket lämnar belastningsöverskottet på den ledande ytan. Inuti det elektriska fältet är noll.

Denna effekt används ofta för att isolera elektrisk och elektronisk utrustning i de yttre fälten, med hjälp av den så kallade Faraday -buren. Buren är gjord av ledande material och omger utrustningen som ska skyddas.

Under stormar fungerar bilar som Faraday -burar genom att skydda passagerare från elektriska stötar.

Taklampor

I belysningssystem, såsom hängande lampor, används det första balansförhållandet för att fixa dem på taket, på golvet eller väggen.

Figur 3. Den utarbetade taklampan som kallas "spindlar" uppfyller det första jämviktstillståndet. Källa: Pixabay.

Böcker och föremål på bord

Objekten som placeras på bord och hyllor uppfyller det första balansförhållandet. Den normala kraften som stödet utövar på föremålen är ansvarig för att kompensera vikten.

Mått på viskositeten hos en vätska

För att bestämma viskositeten hos en vätska är ett sfäriskt objekt, med känd diameter, som kommer att se dess hastighet på grund av motståndet tappas inuti. Sfärens hastighet är konstant och är i dynamisk jämvikt.

En större viskositet hos vätskan, mindre hastigheten med vilken sfären rör sig inuti.

Steg för att tillämpa det första jämviktstillståndet

-Gör ett gratis kroppsdiagram, som visar alla krafter som verkar på kroppen (utelämna vad kroppen utövar på andra).

Det kan tjäna dig: fysik under medeltiden

-Välj ett kartesiskt koordinatsystem och se till att krafterna om möjligt är belägna på någon av axlarna. Den positiva adressen tas vanligtvis i betydelse eller en möjlig rörelse.

-Bestämma de kartesiska komponenterna i varje kraft.

-Tillämpa Newtons andra lag för varje komponent, som fastställts i början, finns det ett system med ekvationer.

-Lös systemet med ekvationer som tas upp i föregående steg.

Löst övningar

- Motion Löst 1

Figurens block m, Den rör sig nedför vinkelplanet θ med konstant hastighet. Beräkna värdet på den kinetiska friktion μ -koefficienten_k, Om blockets massa är m = 5 kg och θ = 37º.

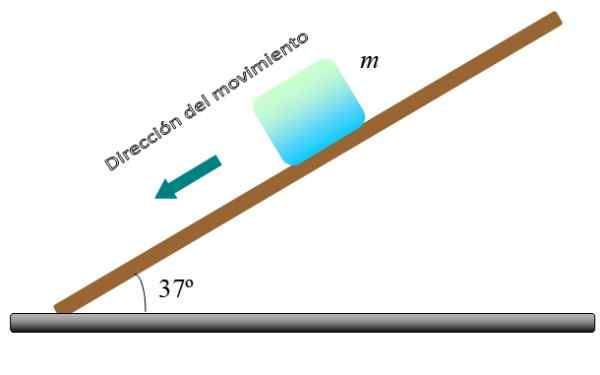Figur 4. Ett block glider med konstant hastighet på ett lutande plan. Källa: f. Zapata.

Lösning

Det första steget är att rita det fria kroppsdiagrammet och välja ett kartesiskt koordinatsystem för att uttrycka varje kraftvektor. Krafterna som verkar på blocket är:

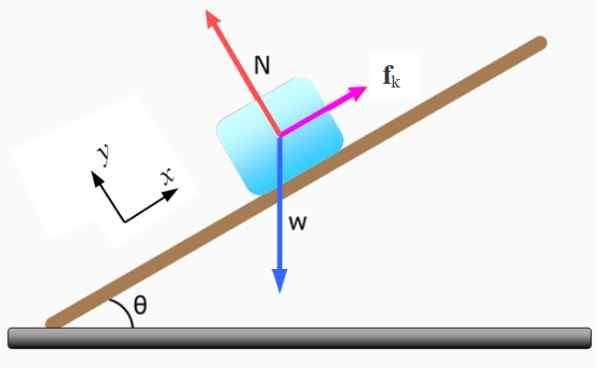Figur 5. Gratis kroppsdiagram för block. Källa: f. Zapata.

-Det normala N Utövas av det lutande planet är det vinkelrätt mot ytan på detta.

-Vikten W Det riktas vertikalt ner.

-Kinetisk friktion F_k som motsätter sig rörelse. Om den inte fanns skulle kroppen röra sig nedförsbacke med en acceleration lika med g.Senθ.

Som vikt W Det är benäget med avseende på de valda koordinataxlarna, den måste delas upp i dess kartesiska komponenter:

W_x = mg.Sen 37º = 5 kg x 9,8 m/s² x sin 37º = 29. 5 n
W_och = mg.cos 37º = 5 kg x 9,8 m/s² x cos 37º = 39.1 n

Newtons andra lag tillämpas nu och matchar varje summa till 0, eftersom blocket saknar acceleration när man rör sig med konstant hastighet:

∑ f_och = N - w_och = 0
∑ f_x = W_x - F_k = 0

Storleken på kinetisk friktion är proportionell mot storleken på det normala, är den kinetiska friktionskoefficienten μ_k Proportionalitetskonstanten.

Det kan tjäna dig: absolut tryck: formel, hur det beräknas, exempel, övningar

F_k = μ_k N

På samma gång:

N = w_och = 39.1 n

Och även:

F_k = W_x

Därför:

29. 5 n = μ_k X 39.1 n

μ_k = 29. 5/39.1 = 0.75

- Motion Löst 2

Beräkna storleken på de spänningar som stöder masstrafikljuset 33 kg, som visas i figuren:

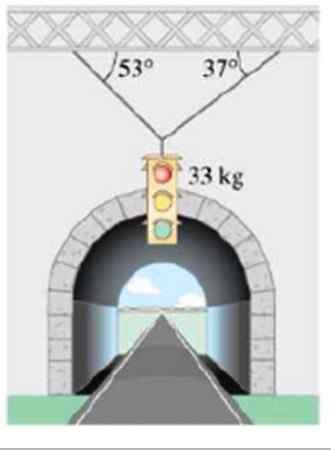Figur 6. En trafikljus hänger med kablar. Källa: Giancoli. Fysik med applikationer.

Lösning

Det fria kroppsdiagrammet görs både för trafikljuset och för knuten som håller kablarna:

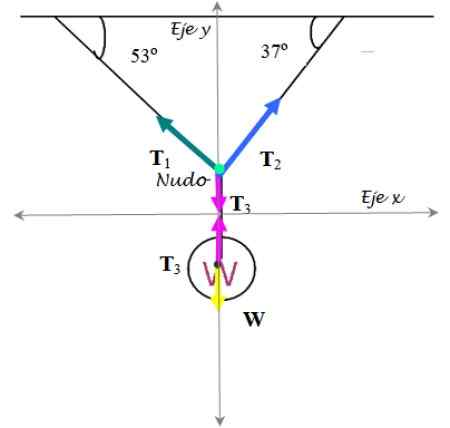Figur 7. Gratis kroppsdiagram för övningen löstes 2. Källa: f. Zapata.

Trafikljus

Om det: spänningen t₃ upp och vikt w ner. Därför:

∑ f_och = W - T₃ = 0

Därför:

T₃ = 33 kg x 9.8 m/s² = 323.4 n

Knut

Spänningarna bryts ned i sina kartesiska komponenter:

∑ f_och = T₁ Sen 53º + T₂ Sen 37º - T₃ = 0
∑ f_x = T₂ Cos 37º - T₁ Cos 53º = 0

Och följande system med linjära ekvationer med två okända erhålls₁  och t₂ :

- 0.6 t₁ + 0.8 t₂ = 0
0.8 t₁ + 0.6 t₂ = 323.4

Lösningen av detta system med ekvationer är: t₁ = 258.7 n och t₂ = 194.0 n

Intresse teman

Jämviktsförhållanden.

Andra jämviktstillstånd.

Referenser

1. Bedford, 2000. TILL. Mekanik för teknik: statisk. Addison Wesley.
2. Figueroa, D. (2005). Serie: Physics for Science and Engineering. Volym 4. Partikelsystem. Redigerad av Douglas Figueroa (USB).
3. Giancoli, D.  2006. Fysik: Principer med applikationer. Sjätte. Ed Prentice Hall.
4. Sears, Zemansky. 2016. Universitetsfysik med modern fysik. 14th. Ed. Volym 1.
5. Wikipedia. Statisk (mekanisk). Återhämtad från: är.Wikipedia.org.