Newtons första lagformler, experiment och övningar

De Newtons första lag, även känd som Inercia lag, Det föreslogs först av Isaac Newton, fysisk, matematiker, filosof, teolog, uppfinnare och alkemist. Denna lag fastställer följande: "Om ett objekt inte utsätts för någon kraft, eller om de krafter som verkar på det avbryts till varandra, kommer det att fortsätta röra sig med konstant snabbhet i en rak linje."

I detta uttalande är nyckelordet fortsättning följer. Om lagens lokaler uppfylls fortsätter objektet med sin rörelse som den hade gjort. Såvida inte en obalanserad kraft dyker upp och ändrar rörelsestillståndet.

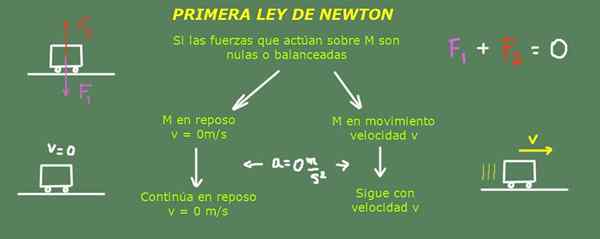
Förklaring av Newtons första lag. Källa: Självgjord.

Detta innebär att om objektet är i vila kommer att fortsätta i vila, förutom om en kraft tar ut det från det tillståndet. Det betyder också att om ett objekt rör sig med en fast hastighet i rak riktning kommer det att fortsätta att röra sig på det sättet. Kommer bara att förändras när en extern agent utövar en kraft på honom och ändrar sin hastighet.

[TOC]

Lagens bakgrund

Isaac Newton föddes i Woolshorpe Manor (Storbritannien) den 4 januari 1643 och dog i London 1727.

Det exakta datumet för vilket Sir Isaac Newton upptäckte sina tre dynamiklagar är inte känt med säkerhet, inklusive den första lagen. Men det är känt att det var långt innan publiceringen av den berömda boken Matematiska principer för naturfilosofi, 5 juli 1687.

Ordboken för den kungliga spanska akademin definierar ordet tröghet på följande sätt:

"Ägs av kropparna av att upprätthålla sin vilande status eller rörelse om det inte är för en styrka handling".

Denna term används också för att bekräfta att alla situationer förblir oförändrade eftersom ingen ansträngning har gjorts för att uppnå det, därför ibland har ordet tröghet rutinkonnotation eller försummelse.

Den pre Newtoniska visionen

Före Newton var de dominerande idéerna de från den stora grekiska filosofen Aristoteles, som hävdade att för ett objekt att förbli i rörelse är det nödvändigt att en styrka agerar på den. När kraften upphör kommer rörelsen också att göra det. Inte så, men även idag tror många det.

Galileo Galilei, en lysande italiensk astronom och fysiker som levde mellan 1564 och 1642, upplevde och analyserade kroppens rörelse.

En av Galileos observationer var att en kropp som glider på en slät och polerad yta med en viss initial impuls, tar längre tid att stoppa och har en större väg i en rak linje, i den utsträckning friktionen mellan kroppen och ytan är lägre.

Det är uppenbart att Galileo hanterade idén om tröghet, men inte formulerade ett uttalande så exakt som Newton.

Kan tjäna dig: Översättningsbalans: Förhållanden, exempel, övningar

Här är några enkla experiment, som läsaren kan utföra och bekräfta resultaten. Observationer kommer också att analyseras enligt den aristoteliska synen på Newtonian Movement and Vision.

Experiment om tröghet

Experiment 1

En låda befordras på golvet och sedan är drivkraften upphängd. Vi observerar att lådan reser en liten resa tills den stannar.

Låt oss tolka det tidigare experimentet och dess resultat, inom ramen för teorierna före Newton och sedan enligt den första lagen.

I den aristoteliska visionen var förklaringen mycket tydlig: lådan stannade eftersom kraften som rörde den avbröts.

I Newtonian -visionen kan lådan på golvet/golvet inte fortsätta röra sig med den hastighet som den hade vid den tidpunkten som styrkan upphängdes, för mellan golvet och lådan finns det en icke -balanserad kraft, vilket gör att hastigheten minskar fram till låda stannar. Detta är friktionskraften.

I detta experiment är lokalerna för Newtons första lag inte uppfyllda, så lådan stannade.

Experiment 2 

Återigen är det lådan på golvet/golvet. Vid detta tillfälle upprätthålls styrkan på lådan, så att friktionskraften kompenserar eller balanseras. Detta händer när vi får lådan att fortsätta ständigt och i en rak riktning.

Detta experiment motsäger inte den aristoteliska visionen om rörelsen: lådan rör sig ständigt eftersom en kraft utövas på den.

Det motsäger inte heller Newtons inställning, eftersom alla krafter som verkar på lådan är balanserade. Låt oss se:

• I den horisontella riktningen är kraften som utövas på lådan densamma och av riktning i motsats till friktionskraften mellan lådan och golvet.
• Då är nettokraften i horisontell riktning noll, det är därför lådan behåller sin hastighet och riktning.

Även i vertikal riktning är krafterna balanserade, eftersom vikten på lådan som är en kraft som pekar vertikalt nere kompenseras exakt av kontaktkraften (eller normal) som jorden utövar på lådan vertikalt uppåt.

Förresten, lådans vikt beror på jordens gravitation attraktion.

Experiment 3

Vi fortsätter med lådan som stöds på golvet. I vertikal riktning är krafterna balanserade, det vill säga att nettokraften är noll. Det skulle verkligen vara mycket förvånande om lådan rörde sig upp.  Men i den horisontella riktningen finns friktionskraft.

Kan tjäna dig: Mekanisk fördel: Formel, ekvationer, beräkning och exempel

Nu, för förutsättningen för Newtons första lag som ska uppfyllas, måste vi minska friktionen till dess minsta uttryck. Detta kan uppnås ganska ungefär om vi letar efter en mycket slät yta som vi sprayade silikonolja.

Eftersom silikonolja minskar friktionen nästan till noll, så när denna låda är horisontellt kommer den att bibehålla sin hastighet och riktning med en lång sektion.

Det är samma fenomen som inträffar med en åkare på en isspår eller med ishockeyskivan när de körs och släpper sitt eget konto.

I de beskrivna situationerna, där gnuggarna.

I den aristoteliska visionen kunde detta inte hända, för enligt denna naiva teori inträffar rörelsen bara när det finns en nettokraft på objektet i rörelse.

Isytan kan övervägas med mycket liten friktion. Källa: Pixabay.

Förklaring av Newtons första lag

Tröghet och massa

Massan är en fysisk mängd som indikerar mängden materia som innehåller en kropp eller föremål.

Massan är då en inre egenskap av materia. Men materia består av atomer, som har en massa. Atommassan är koncentrerad i kärnan. Det är protoner och neutroner i kärnan som praktiskt definierar atomens massa och materia.

Massan mäts vanligtvis i kilogram (kg), det är den grundläggande enheten för International Units System (SI).

Prototypen eller referensen för KG är en platina- och iridiumcylinder som lagras på International Office of Wights and Measures in Sèvres i Frankrike, även om den 2018 var kopplad till Planck -konstanten och den nya definitionen träder i kraft från 20 maj 2019 2019.

Det händer att tröghet och deg är relaterade. En större massa, större tröghet har ett objekt. Det är mycket svårare eller dyrt när det gäller energi att förändra tillståndet för en mer massiv än en annan mindre massiv.

Exempel

Till exempel krävs mycket mer styrka och mycket mer arbete för att ta en låda med en ton (1000 kg) från vila än ytterligare ett kilo (1 kg). Det är därför det vanligtvis sägs att den första har mer tröghet än den andra.

På grund av förhållandet mellan tröghet och massa insåg Newton att hastigheten inte är representativ för rörelsestillståndet. Det är därför han definierade ett belopp som kallas rörelse antingen Momentum som betecknas med texterna p Och det är produkten av massan m För snabbhet v:

Det kan tjäna dig: Grashof Law: Cases, Mekanismer, exempel, applikationer

 p = m v

Det djärva i p och i v De indikerar att det här är vektorens fysiska mängder, det vill säga de är mängder med storlek, riktning och mening.

Istället massan m Det är en skal kvantitet, som tilldelas ett nummer som kan vara större än eller lika med noll, men aldrig negativt. Fram till nutid har ett objekt med negativ massa inte hittats i universum känt.

Newton förde sin fantasi och abstraktion till det extrema och definierade samtalet Fri partikel. En partikel är en materiell punkt. Det vill säga, det är som en matematisk punkt men med massa:

En fri partikel är den partikeln som är så isolerad, så långt från ett annat objekt i universum att ingenting kan utöva viss interaktion eller styrka över den.

Senare fortsatte Newton att definiera tröghetsreferenssystemen, som kommer att vara de där deras tre lagar tillämpas. Här är definitionerna enligt dessa koncept:

Tröghetsreferenssystem

Varje koordinatsystem kopplat till en fri partikel, eller som överförs med konstant hastighet med avseende på den fria partikeln kommer att vara ett tröghetsreferenssystem.

Newtons första lag (tröghetslag)

Om en partikel är fri, har den en konstant mängd rörelse med avseende på ett tröghetsreferenssystem.

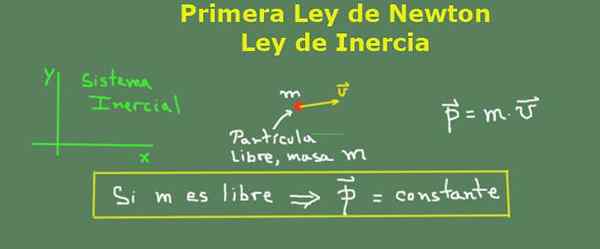Newtons första lag och mängden rörelse. Källa: Självgjord.

Löst övningar

Övning 1

Ett hockeyalbum är 160 gram på isbanan på 3 km/h. Hitta din mängd rörelse.

Lösning

Albumets massa i kilogram är: M = 0.160 kg.

Hastigheten i meter över sekund: V = (3/3.6) m/s = 0.8333 m/s

Mängden rörelse eller momentum p beräknas enligt följande: p = m*v = 0.1333 kg* m/s,

Övning 2

Friktion på föregående album betraktas som Void, så momentumet bevaras medan ingenting förändrar albumets raka kurs. Det är emellertid känt att två krafter agerar på albumet: skivans vikt och kontaktkraften eller normalt som golvet utövar på den.

Beräkna värdet på normal kraft i newton och dess riktning.

Lösning

När momentumet bevaras måste den resulterande kraften på hockeyalbumet vara noll. Viktpunkterna vertikalt ner och ok: p = m *g = 0.16 kg * 9.81 m/s²

Den normala kraften måste nödvändigtvis motverka vikten, så den måste registrera sig vertikalt och dess storlek blir 1.57 n.

Intresseartiklar

Newtons lagexempel i verkliga livet.

Referenser

1. Alonso m., Finn e. Fysikvolym I: Mekanik. 1970. Inter -American Education Fund S.TILL.
2. Hewitt, s. Konceptuell fysisk vetenskap. Femte upplagan. Pearson. 67-74.
3. Young, Hugh. Universitetsfysik med modern fysik. 14: e upplagan. Pearson. 105 - 107.