Påskprinciphistoria, applikationer, exempel

han Pascalprincip, o Pascal lag, konstaterar att en förändring i trycket på en vätska som är begränsad i någon av dess punkter överförs utan förändring av alla andra punkter inom vätskan.

Denna princip upptäcktes av den franska forskaren Blaise Pascal (1623 - 1662). På grund av vikten av bidrag från Pascal till vetenskapen har tryckenheten i det internationella systemet utsetts till sin ära.

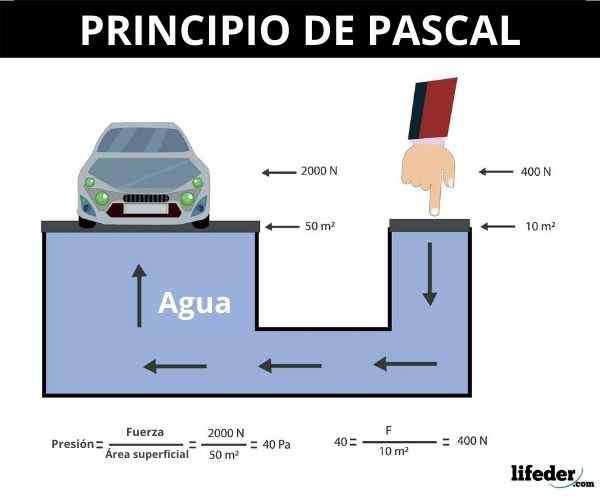
Eftersom trycket definieras som kvoten mellan kraften vinkelrätt mot ett område mellan dess område, är 1 Pascal (PA) lika med 1 Newton / m².

[TOC]

Historia

För att verifiera dess princip utformade Pascal en ganska överväldigande demonstration. Han tog en ihålig sfär och genomborrade på flera platser, satte mössor i alla hål utom i ett, för vilka han fyllde den med vatten. I detta placerade han en spruta med en kolv.

Genom att tillräckligt öka trycket i kolven skjuts locken samtidigt, eftersom trycket överförs lika till alla vätskepunkter och i alla riktningar, vilket visar Pascal -lagen.

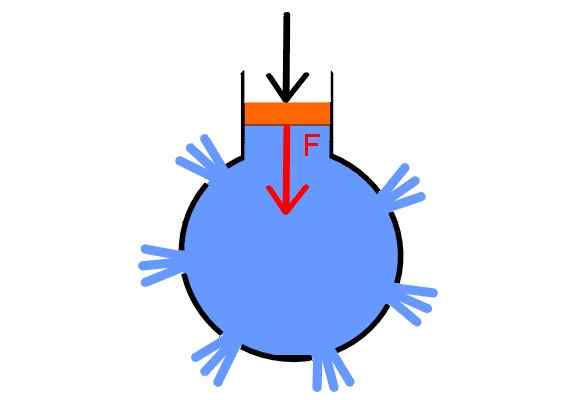Pascalspruta. Källa: Wikimedia Commons.

Blaise Pascal hade ett kort liv, präglat av sjukdomen. Det otroliga räckvidden för att hans sinne ledde till att han undersökte i olika aspekter av naturen och filosofin. Hans bidrag var inte begränsade till att studera vätskans beteende, Pascal var också en pionjär inom datoranvändning.

Och vid 19 års ålder skapade Pascal en mekanisk kalkylator för sin far att använda henne i sitt arbete i Frankrikes skattesystem: Pascalina.

Tillsammans med sin vän och kollega formade den stora matematikern Pierre of Fermat teorin om sannolikheter, oumbärlig inom fysik och statistik. Pascal dog i Paris, vid 39 års ålder.

Förklaring av Pascal -principen

Nästa experiment är ganska enkelt: ett U -rör är fyllt med vatten och lock placeras i varje ände som kan glida smidigt och enkelt, som en kolv. Det är tryck mot den vänstra kolven som sjunker lite och det observeras att den till höger stiger, skjuts av vätskan (nedre figuren).

Kan tjäna dig: Andromeda: upptäckt, ursprung, egenskaper, struktur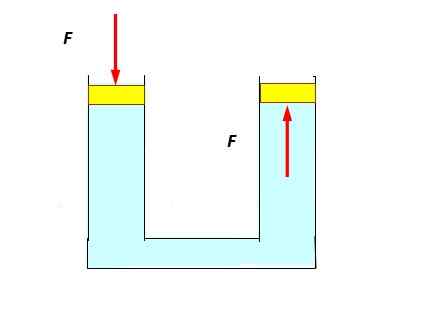Tillämpning av Pascal -principen. Källa: Självgjord.

Detta händer eftersom trycket överförs utan någon minskning till hela vätskan, inklusive de som är i kontakt med höger kolv.

Vätskor som vatten eller olja är inkomprimerbara men samtidigt har molekylerna tillräckligt med rörelsefrihet, vilket gör det möjligt för trycket att fördelas på höger kolv.

Tack vare detta får den högra kolven en kraft som är exakt densamma i storlek och riktning som den applicerades till vänster, men i motsatt riktning.

Trycket i en statisk vätska är oberoende av behållarens form. Det kommer omedelbart att demonstreras att trycket varierar linjärt med djupet och principen för Pascal är en följd av detta.

En förändring av trycket när som helst gör trycket vid en annan punkt förändras i samma mängd. Annars skulle det finnas ett extra tryck som skulle flyta vätskan.

Förhållandet mellan tryck och djup

En vilovätska utövar en kraft på väggarna i behållaren som innehåller den och även på ytan av alla objekt som är nedsänkta i den. I experimentet av pascal spruta ser man att vattenstänket kommer ut vinkelrätt Till sfären.

Vätskorna fördelar kraften vinkelrätt på ytan som den verkar, så det är bekvämt att införa konceptet med genomsnittligt tryck P_m Som den vinkelräta kraften utövas F_⊥ Efter området TILL, vars enhet är Pascal:

P_m = F_⊥ Till

Trycket ökar med djupet. Du kan se en liten del av statisk jämviktsvätska och tillämpa Newtons andra lag:

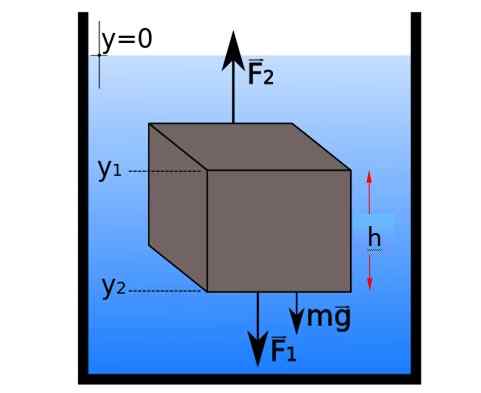Gratis kroppsdiagram över en liten del av statisk jämvikt med en kubformad. Källa: E-XUAO [CC BY-SA 4.0 (https: // CreativeCommons.Org/licenser/BY-SA/4.0)]

Horisontella krafter avbryts av par, men i vertikal riktning grupperas krafterna enligt följande:

∑f_och = F₂ - F₁ - mg = 0 → F₂ - F₁ = mg

Uttrycka degen i termer av densitet ρ = massa /volym:

P₂.A- p₁.A = ρ X Volym x g

Volymen på den vätskeddelen är produkten vid x h:

Det kan tjäna dig: andra lagen om termodynamik: formler, ekvationer, exempel

TILL.(P₂ - P₁) = ρ X a x h x g

ΔP = ρ.g.h   Grundläggande sats för hydrostatisk

Ansökningar

En traktorgeln använder Pascal -principen för att lyfta stora pesos

Pascal -principen har använts för att bygga många enheter som multiplicerar styrka och underlättar uppgifter som att lyfta pesos, stämpla på metall eller pressa föremål. Bland dem är:

-Den hydrauliska pressen

-Bilbromssystemet

-Mekaniska spade och mekaniska armar

-Den hydrauliska katten

-Kranar och hissar

Låt oss sedan se hur Pascal -principen gör att små krafter förvandlas till stora krafter för att utföra alla dessa verk. Den hydrauliska pressen är det mest karakteristiska exemplet och kommer att analyseras nedan.

Den hydrauliska pressen

För att bygga en hydraulisk press tas samma enhet i den övre figuren, det vill säga en U -formad behållare, som vi redan vet att samma kraft överförs från en kolv. Skillnaden är storleken på kolvarna och det är detta som får enheten att fungera.

Följande figur visar Pascal -principen i handling. Trycket är detsamma vid alla vätskepunkter, både i den lilla och stora kolven:

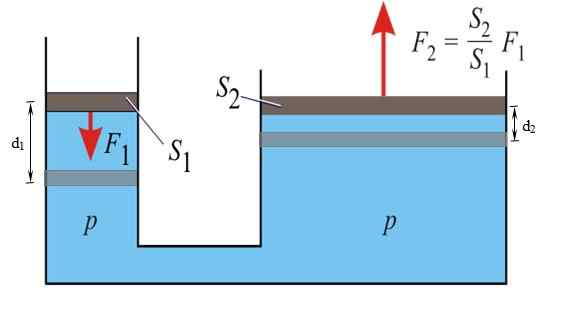Hydraulisk pressprogram. Källa: Wikimedia Commons.

p = f₁ / S₁ = F₂ / S₂

Storleken på kraften som överförs till den stora kolven är:

F₂ = (S₂ / S₁). F₁

Gillar₂ > S₁, resulterar i f₂ > F₁, Därför har utgångskraften multiplicerats i den faktor som ges av kvoten mellan områdena.

Exempel

Det här avsnittet visar applikationsexempel.

Hydraulbromsar

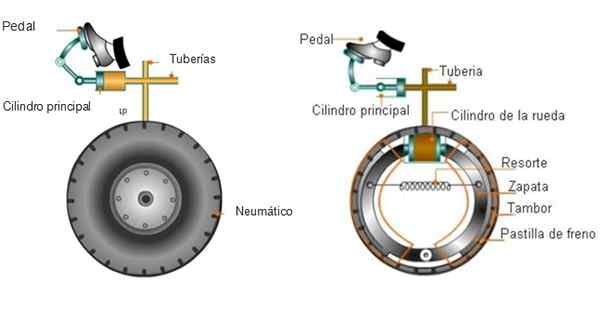
Bilbromsar använder Pascal -principen genom en hydraulvätska som fyller vissa rör anslutna till hjulen. När du behöver stoppa tillämpar föraren en kraft genom att förtrycka bromspedalen och generera ett tryck på vätskan.

I den andra änden skjuter trycket bromsbeläggarna mot trumman eller bromsskivorna som svänger ihop med hjulen (inte med däcken). Den resulterande friktionen får skivan att stoppa, också bromsar hjulen.

Kan tjäna dig: mekaniska vågor: egenskaper, egenskaper, formler, typerHydraulisk bromssystem. Källa: f. Zapata

Mekanisk fördel med den hydrauliska pressen

I den hydrauliska pressen i den nedre figuren måste ingångsarbetet vara lika med utgångsarbetet så länge friktion inte beaktas.

Ingångsstyrkan F₁ gör kolven att resa till avstånd d₁ När du går ner, medan utgångskraften F₂ Tillåter en D₂ av kolven som går upp. Om det mekaniska arbetet som görs av båda krafterna är detsamma:

F₁.d₁ = F₂. d₂

Den mekaniska fördelen m är kvoten mellan storleken på ingångs- och utgångskraften:

M = f₂/F₁ = D₁/d₂

Och som visas i föregående avsnitt kan det också uttryckas som kvoten mellan områdena:

F₂/F₁ = S₂ / S₁

Det verkar som om arbete görs gratis men det skapar inte riktigt energi med den här enheten, eftersom den mekaniska fördelen erhålls på bekostnad av förskjutningen av den lilla kolven D₁.

Så för att optimera prestanda läggs ett ventilsystem till enheten på ett sådant sätt att utgångskolven höjs tack vare korta impulser på ingångskolven.

På detta sätt pumpar operatören av en garage hydraulisk katt flera gånger för att gradvis lyfta ett fordon.

Träning löst

I den hydrauliska pressen i figur 5 är kolvområdena 0.5 kvadratmeter (liten kolv) och 25 kvadratmeter (stor kolv). Hitta:

a) Den mekaniska fördelen med denna press.

b) den nödvändiga kraften för att lyfta en belastning på 1 ton.

c) Avståndet vid vilket ingångsstyrkan måste agera för att lyfta nämnda belastning i 1 tum.

Uttrycka alla resultat i enheter i det brittiska systemet och det internationella systemet om.

Lösning

a) Den mekaniska fördelen är:

M = f₂/F₁ = S₂/S₁ = 25 in² / 0.5 i² = 50

b) 1 ton motsvarande 2000 lb-kraft. Den nödvändiga styrkan är f₁:

F₁ = F₂ / M = 2000 lb-kraft / 50 = 40 lb-kraft

För att uttrycka resultatet i det internationella systemet krävs följande omvandlingsfaktor:

1 pund-kraft = 4.448 n

Därför är F1: s storlek 177.92 n.

c) M = D₁/d_{2 →} d₁ = M.d₂ = 50 x 1 tum = 50 in

Den nödvändiga omvandlingsfaktorn är: 1 in = 2.54 cm

d₁ = 127 cm = 1.27 m

Referenser

1. Bauer, w. 2011. Fysik för teknik och vetenskap. Volym 1. MC Graw Hill. 417-450.
2. Högskolefysik. Pascals principie. Återhämtad från: OpenTextbc.Växelström.
3. Figueroa, D. (2005). Serie: Physics for Science and Engineering. Volym 4. Vätskor och termodynamik. Redigerad av Douglas Figueroa (USB). 4 - 12.
4. Rex, a. 2011. Fysikens grunder. Pearson. 246-255.
5. Tippens, s. 2011. Fysik: koncept och applikationer. Sjunde upplagan. McGraw Hill.301-320.