Fyrkantig prisma

Vi förklarar vad som är ett fyrkantigt prisma, dess egenskaper, ansikten, vertikaler, kanter, hur man beräknar volym, exempel och övningar löst

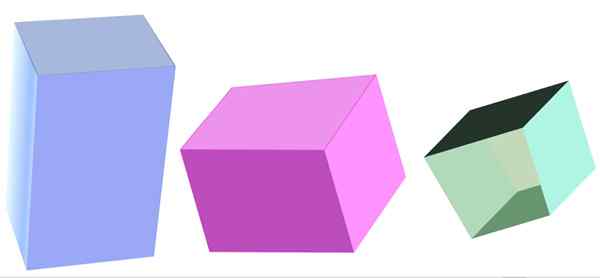
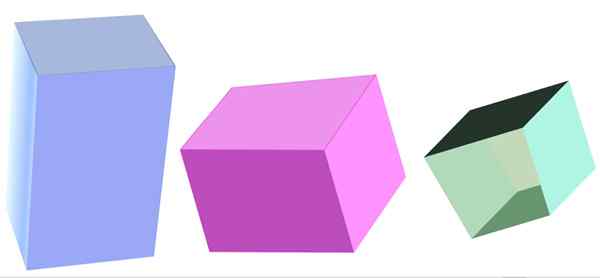Olika typer av fyrkantigt prisma. Källa: f. Zapata

Vad är ett fyrkantigt prisma?

han Fyrkantig prisma Det är en tre -dimensionell geometrisk figur i Polyhedros -familjen. Den består av två lika och parallella ansikten, med formen av en fyrkant, som bas och fyra parallellogram på sidorna, för totalt sex ansikten.

Det finns flera kriterier för att klassificera dem, eftersom det finns många möjligheter för formen på ansikten och lutningen. Till exempel finns det Raka hemkörningsprismor och den lutande fyrkantiga prismor.

I det första fallet är sidorna vinkelrätt mot basen, och sedan är de rektanglar eller rutor. I det andra fallet är sidans ansikten benägna med avseende på basen, därför kan de inte vara rektanglar eller fyrkantiga.

Dessutom kan fyrkantiga prisma vara regelbundna eller oregelbundna, beroende på basen är en regelbunden eller oregelbunden fyrkantig fyrkantig. Den vanliga fyrkantiga är torget, vars fyra sidor och dess fyra vinklar mäter samma .

Ett exempel på Special Home Run Prism är Parallelepiped, vars baser är parallellogram. Formerna på lådorna och tegelstenarna är inspirerade av fyrkantiga prismor, så bra exempel på hur man använder denna geometriska figur i praktiska tillämpningar är.

Egenskaper för det fyrkantiga prismen

Bland de viktigaste egenskaperna hos det fyrkantiga prismen är följande:

• Deras ansikten har en polygonform.
• Den har totalt 6 ansikten (2 baser och 4 sidor), 12 kanter eller kanter och 8 vertikaler (hörn).
• Sidans ansikten kan formas som: fyrkantig, rektangel, parallellogram, rhombus eller rhomboid.
• Sidorna kan vara raka (form 90º vinkel med baserna) eller lutande (det finns en vinkel mindre än 90º på den inre sidan).
• De laterala ansikten av raka prismor kan bara vara fyrkantiga eller rektanglar.
• Prismbaserna får också namnet på riktlinjer.
• Om basen är en vanlig fyrkantig är det fyrkantiga prismen också regelbunden. Eftersom en platt figur är regelbunden om alla sidor har samma mått, är den enda möjligheten att baserna är fyrkantiga.
• När priset är någon annan fyrkantig annorlunda än torget, betraktas prismen oregelbunden.
• Det vanliga fyrkantiga prismen kan registreras i en cylinder.

Kan tjäna dig: Inferential Statistics: Historia, Egenskaper, vad är det för, exempel

Element i det fyrkantiga prismen

De fem elementen i det fyrkantiga prismen är vanliga för alla prismor:

• Baser, består av två identiska och parallella fyrkantiga.
• Laterala ansikten, är de fyra parallellogrammen som gränsar till figuren.
• Häckar eller hörn, vanliga punkter som har tre angränsande sidor av prismen.
• Kanter eller kanter, gemensamt segment som har två angränsande ansikten.
• Höjd: Det är längden på ett vinkelröst segment med ändar i baserna. När prismen är rak sammanfaller höjden med måttet på sidokanterna.
• Rak sektion, korsningsområdet mellan prismen och ett plan som bildar 90º med sidokanterna.

Följande bild visar vart och ett av dessa element för ett rak fyrkantigt prisma:

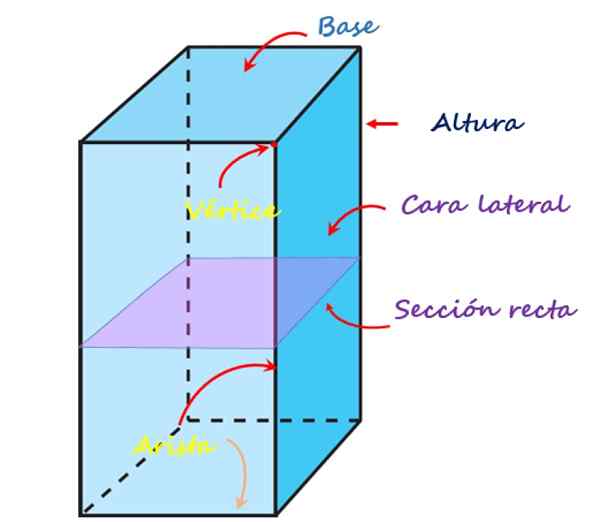Elementen i det fyrkantiga prismen. Källa: f. Zapata

Ansikten, vertikaler och kanter

Av stor betydelse för att studera det fyrkantiga prismen är ansikten, vertikalerna och kanterna:

Inslag

Prismets ansikten gör totalt 6: de två identiska baserna i form av en fyrkantig och de fyra sidosidorna eller ansikten i form av parallellogram.

Häckar

De är hörnen på figuren, punkten där tre angränsande ansikten kommer.

Kanter

De är skärningssegmenten mellan prisma ansikten. Kanterna klassificeras som:

• Baskanter, Vanliga segment mellan baser och sidoytor.
• Sidokanter, Som namnet antyder är de de vanliga segmenten bland sidosytorna.

Den översta figuren visar de två typerna av kanter, avsedda med olika färgpilar. Antalet kanter n_TILL kan bestämmas med Euler teorem av polyhedros, som relaterar antalet kanter till ansikten n_C och vertikaler n_V:

Kan tjäna dig: matematiska funktioner

N_TILL = N_C + N_V −2

För det fyrkantiga prismen n_C = 6 och n_V = 8, därför:

N_TILL = 6 + 8 −2 = 12

Därför är antalet kanter eller kanter på det fyrkantiga prismen 12.

Hur man beräknar volymen på ett fyrkantigt prisma?

Prismens volym förstås som den del av det utrymme som låsts av det och mäts i kubiska enheter, som kan vara kubikmeter, kubikcentimeter, kubikfot eller annat lämpligt, förutsatt att de är av längd till kuben.

Volym V är alltid ett positivt belopp, och i fallet med något fyrkantigt prisma ges det av produkten mellan basens bas till_b och höjd h:

V = a_b × h

Yo) Regelbunden fyrkantig prisma volym

Eftersom baserna är fyrkantiga och kvadratet på kvadratet är dess sida ℓ fyrkantig:

TILL_b = ℓ²

Sedan är volymen på prisma vars höjd är "H":

V = ℓ² × h

Ii) Oregelbunden fyrkantig prisma volym

Det beror på basens form och höjden "h" för prisma:

1.- Rektangulär basprism

Områdets rektangel "A" och "B" är:

TILL_b = A × B

Så volymen är:

V = a × b × h

2.- Romboidal Base Prism

Rhombus -området är semi -produkten från dess "D" och "D" -diagonaler:

Och volymen är:

3.- Romboid -formad basprism

Det rhomboid -formade basområdet är produkten från dess bas "B" och dess relativa höjd "h_r”Till denna bas, som är det vinkelräta segmentet som går från denna bas till den parallella sidan till den.

TILL_b = B × h_r

Därför är priset av prisma med denna bas:

Kan tjäna dig: vad är statistikområdet? (Med exempel)

V = b × h_r × h

4.- Trapesformad basprism

Eftersom trapezoidområdet är semi -sätet för de parallella sidorna "A" och "B", multiplicerat med dess höjd "C":

Volymen på det trapezoidala prismen är:

5.- Trapezoidformad basprism

Området för en symmetrisk trapezoid är halvprodukten för dess diagonaler D och D, därför:

I det här fallet är prismaens volym:

Träning löst

En trapezoidal basfyrkantig prisma har en volym på 648 cm³. Trapezoidens parallella sidor mäter a = 10 cm och b = 5 cm, medan trapeshöjden är c ​​= 6 cm. Med dessa uppgifter hitta priset på höjden.

Lösning

Eftersom basens dimensioner har kan ditt område enkelt beräknas:

Och av formeln:

V = a_b × h

"H" rensas, prismen, eftersom dess volym är känd:

H = v/ a_b = 648 cm³ / 45 cm² = 14.4 cm

Exempel

Rektangulärt prisma eller kub

De sex ansikten av detta raka prisma är fyrkantiga eller rektangulära. Lådorna är exempel på rektangulära prismor, en form som också används i många föremål och konstruktioner som byggnader.

Kub

En kub är ett vanligt fyrkantigt prisma, vars sex sidor är formade som en fyrkant, till exempel en tärning eller det välkända Rubiks kubspel.

Kuben är en del av gruppen av platoniska fasta ämnen, geometriska figurer som uppfyller två villkor. Den första är att varje ansikte är en vanlig polygon och den andra är att varje toppunkt har gemensamt samma antal ansikten.

Kuben uppfyller båda förhållandena, eftersom deras ansikten har en fyrkantig form, vilket är en vanlig polygon. Och i var och en av de åtta vertikalerna i kuben är tre ansikten av samma konvergera.

De återstående platoniska fasta ämnena är tetrahedronen, octahedronen, dodekahedro och ikosaedro.