Politropiska processegenskaper, applikationer och exempel

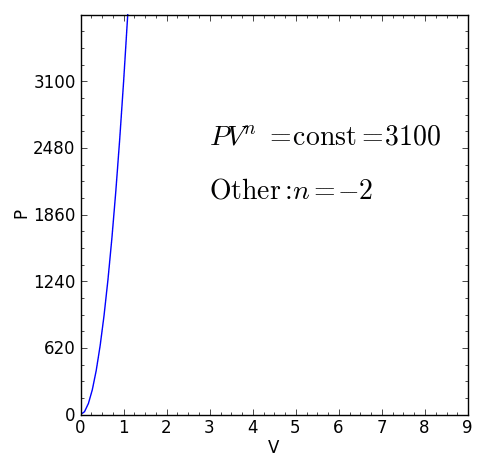
En Politropisk process Det är en termodynamisk process som uppstår när förhållandet mellan tryck P och volymen V getts av P.Vⁿ Det förblir konstant. Exponenten n Det är ett verkligt antal, vanligtvis mellan noll och oändlighet, men det kan i vissa fall vara negativt.

Värdet av n få namnet på Politropiindex Och det är viktigt att lyfta fram att under en polytropisk termodynamisk process sa att index måste upprätthålla ett fast värde, annars kommer processen inte att betraktas som polytropisk.

Figur 1. Karakteristisk ekvation av en polytropisk termodynamisk process. Källa: f. Zapata.

[TOC]

Egenskaper hos polytropiska processer

Vissa karakteristiska fall av polytropiska processer är: 

- Den isotermiska processen (vid konstant T -temperatur), där exponenten är n = 1.

- En isobarisk process (konstant tryck p), i detta fall n = 0.

- Den isokoriska processen (till volym V -konstant), för vilken n =+∞.

- Adiabatiska processer (till konstant entropi), där exponenten är n = y, är y den adiabatiska konstanten. Denna konstant är kvoten mellan värmekapaciteten vid konstant tryck CP dividerat med värmekapaciteten vid konstant CV -volym:

γ = CP/CV

- Någon annan termodynamisk process som inte är något av de tidigare fallen. Men följer P.Vⁿ = ctte Med verkligt och konstant polytropiskt index n Det kommer också att vara en polytropisk process.

figur 2. Olika karakteristiska fall av polytropiska termodynamiska processer. Källa: Wikimedia Commons.

Ansökningar

En av de viktigaste tillämpningarna av den polytropiska ekvationen är för beräkningen av det arbete som gjorts av ett stängt termodynamiskt system, när det passerar från ett initialt tillstånd till ett annat ändamål på ett kvasi -statiskt sätt, det vill säga efter en följd av jämviktstillstånd.

Arbeta i polytropiska processer för olika värden på N

För n ≠ 1

Mekaniskt arbete som utförs av ett stängt termodynamiskt system beräknas genom uttryck:

W = ∫p.Dv

Kan tjäna dig: Diamagnetism: Material, applikationer, exempel

Där p är trycket och v volymen.

Liksom i fallet med en polytropisk process är förhållandet mellan tryck och volym:

P.V ⁿ = konstant = c

Rensa p i det tidigare uttrycket för att ersätta det i uttrycket av arbete:

P = c /V ⁿ

Du har gjort det mekaniska arbetet under en polytropisk process, som börjar i ett initialt tillstånd 1 och slutar i det slutliga tillståndet 2. Allt detta visas i följande uttryck:

Om n ≠ 1, har du:

Eftersom de initiala och slutliga tillstånden är väl definierade, bestäms dessutom konstanten också av följande uttryck:

C = p₁ V₁ⁿ = P₂ V₂ⁿ

Genom att ersätta värdet på konstanten i uttrycket av arbetet erhålls:

W = (p₂ V₂ - P₁ V₁)/(1-n)

I händelse av att arbetsämnet kan modelleras som en idealisk gas har följande tillståndsekvation:

P.V = m.R.T

Där m är antalet mol av idealisk gas och r är den universella konstanten för gaser.

För en idealisk gas som följer en polytropisk process med ett polytropindex som skiljer sig från enheten och som passerar från ett tillstånd med initial temperatur T₁ till ett annat tillstånd med temperatur t₂ Arbetet ges av följande formel:

W = m r (t₂ - T₁)/(1-n)

För N → ∞

Enligt formeln för det arbete som erhållits i föregående avsnitt är arbetet med en polytropisk process med n = ∞ noll, eftersom uttrycket av arbete är uppdelat mellan oändlighet och därför tenderar resultatet att noll.

Ett annat sätt att nå detta resultat är att starta från P -förhållandet₁ V₁ⁿ = P₂ V₂ⁿ, som kan skrivas om enligt följande:

(P₁/P₂) = (V₂/V1)ⁿ

Ta N-Thicker Root i varje medlem du får:

(V₂/V1) = (P₁/P₂)^(1/n)

I det fall N → ∞ måste du (v₂/V1) = 1, vilket betyder att:

Kan tjäna dig: ceded värme: formler, hur man beräknar den och lösta övningar

V₂ = V₁

Det vill säga, volymen förändras inte i en polytropisk process med N → ∞. Därför är DV -volymdifferensen i integralen av mekaniskt arbete 0. Dessa typer av polytropiska processer är också kända som processer isokorisk, o Processer i konstant volym.

För n = 1

Återigen har vi uttrycket för arbete:

W = ∫p DV

När det gäller en polytropisk process med n = 1 är förhållandet mellan tryck och volym:

P v = konstant = c

Genom att rensa P i det tidigare uttrycket och ersättningen har du arbetet gjort för att gå från det ursprungliga tillståndet 1 till sluttillståndet 2:

W = ∫12p dv = ctte ∫12 v^( - 1) dv = ctte (ln (v2) - ln (v1))

Det vill säga:

W = c ln (v₂/V₁).

Eftersom de initiala och slutliga staterna är väl bestämda, kommer CTTE också. Det vill säga:

C = p₁ V₁ = P₂ V₂

Slutligen är följande användbara uttryck tillgängliga för att hitta det mekaniska arbetet för ett polyitropiskt stängt system där n = 1.

W = p₁ V₁ ln (v₂/V₁) = P₂ V₂ ln (v₂/V₁)

Om arbetsämnet består av m Mullvad med idealisk gas, då kan den ideala gasekvationen appliceras: p v = m.R.T.

I detta fall, som P.V₁ = CTTE, en polytropisk process med n = 1 är en process vid konstant T -temperatur (isotermisk), så att följande uttryck för arbete kan erhållas:

W = m r t₁ ln (v₂/V₁) = m r t₂ ln (v₂/V₁)

Figur 3. En caramban smälter, exempel på isotermisk process. Källa: Pixabay.

Exempel på polytropiska processer

- Exempel 1

Anta en cylinder med en rörlig kolv full med ett kilo luft. Ursprungligen upptar luften en volym v₁= 0,2 m³ vid ett tryck s₁= 400 kPa. En polytropisk process följs med n = y = 1,4, vars slutliga tillstånd har tryck p₂ = 100 kPa. Bestäm det arbete som gjorts av luften på kolven.

Lösning

När polytropiindexet är lika med den adiabatiska konstanten finns det en process där arbetsämnet (luft) inte utbyter värme med miljön och ändrar därför inte entropi.

Det kan tjäna dig: Tredje lagen om termodynamik: formler, ekvationer, exempel

För luft, en idealisk diatomisk gas, har du:

y = CP/CV, med CP = (7/2) R och CV = (5/2) R

Så:

γ = 7/5 = 1,4

Med hjälp av uttrycket av den polytropiska processen kan den slutliga volymen av luften bestämmas:

V₂ = [P₂ V₁^1.4)/P₂]^(1/1.4) = 0,54 m³.

Nu finns det villkor för att tillämpa arbetsformeln som görs i en polytropisk process för n ≠ 1 som erhållits ovan:

W = (p₂ V₂ - P1 v1)/(1-n)

Att ersätta lämpliga värden är:

W = (100 kPa 0,54 m³ - 400 kPa 0,2 m³)/(1 - 1,4) = 65,4 kJ

- Exempel 2

Anta samma cylinder i exempel 1, med en rörlig kolv full med ett kilo luft. Ursprungligen upptar luften en volym V1 = 0,2 m³ Vid ett tryck P1 = 400 kPa. Men till skillnad från det föregående fallet expanderar luften isotermiskt för att nå ett slutligt tryck P2 = 100 kPa. Bestäm det arbete som gjorts av luften på kolven.

Lösning

Som tidigare sett är isotermiska processer polytropiska processer med index n = 1, så det uppfylls att:

P1 V1 = P2 V2

På detta sätt kan den slutliga volymen lätt lossas för att få:

V2 = 0,8 m³

Sedan använder du uttrycket av det arbete som tidigare erhållits för fallet n = 1 måste du arbeta i luften på kolven i denna process är:

W = P1 V1 LN (V2/V1) = 400000 PA × 0,2 M³ ln (0,8/0,2) = 110,9 kJ.  

Referenser

1. Bauer, w. 2011. Fysik för teknik och vetenskap. Volym 1. MC Graw Hill.
2. Cengel och. 2012. Termodynamik. Sjunde upplagan. McGraw Hill.
3. Figueroa, D. (2005). Serie: Physics for Science and Engineering. Volym 4. Vätskor och termodynamik. Redigerad av Douglas Figueroa (USB).
4. López, c. Termodynamikens första lag. Återhämtat sig från: kulturientifica.com.
5. Riddare, r. 2017. Fysik för forskare och teknik: En strategistrategi. Pearson.
6. Serway, R., Vule, c. 2011. Fysikens grunder. 9na ed. Cengage Learning.
7. Sevilla universitet. Termiska maskiner. Återhämtat sig från: Laplace.oss.är.
8. Wikiwand. Politropisk process. Återhämtat sig från: wikiwand.com.