Dynamiska programmeringsegenskaper, exempel, fördelar, nackdelar

De Dynamisk programmering Det är en algoritmmodell som löser ett komplext problem genom att dela upp den i delproblem och lagra sina resultat för att undvika att beräkna dessa resultat.

Detta program används när problem kan delas in i liknande delproblem, så att deras resultat kan återanvändas. För de flesta majoriteten används detta program för optimering.

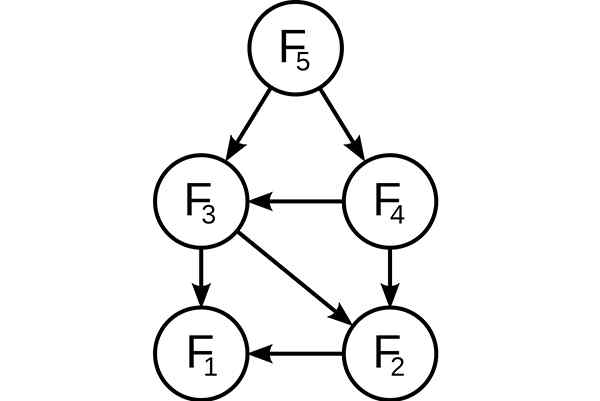
Dynamisk programmering. Delproblem överlagrade i Fibonacci -successionen. Källa: Wikimedia Commons, på: Användare: DCOATZEE, spårad av användare: Stannered / Public Domain

Innan den tillgängliga subproblemet löser det tillgängliga delen kommer den dynamiska algoritmen att försöka undersöka resultaten från de tidigare upplösta delproblemen. Subproblems Solutions kombineras för att uppnå den bästa lösningen.

Istället för att beräkna samma subproblema om och om igen kan din lösning lagras i något minne när du först möter detta subproblem. När det visas igen under lösningen av ett annat delproblem kommer lösningen som redan lagras i minnet att tas.

Detta är en underbar idé att korrigera tid med minnet, där när du använder ytterligare utrymme kan du förbättra den tid som krävs för att hitta en lösning.

[TOC]

Egenskaper för dynamisk programmering

Följande väsentliga egenskaper är de som ett problem kan tillämpas för dynamisk programmering:

Optimal understruktur

Denna egenskap uttrycker att ett optimeringsproblem kan lösas genom att kombinera de optimala lösningarna av de sekundära problemen som utgör det. Dessa optimala understrukturer beskrivs genom rekursion.

I en graf kommer till exempel en optimal understruktur att presenteras på den kortaste rutten som går från ett toppunkt till ett toppunkt T:

Det vill säga, på denna kortaste väg r kan du ta alla mellanliggande vertex i. Om R verkligen är den kortaste vägen, kan den delas upp i Subrutas R1 (från S till I) och R2 (från I till T), så att det i sin tur är de kortaste vägarna mellan motsvarande vertikaler.

För att hitta de kortaste rutterna kan du enkelt formulera lösningen rekursivt, vilket är vad Floyd-Warshall-algoritmen gör.

Överlagrade delproblem

Underproblemen måste vara litet. Det vill säga varje rekursiv algoritm som löser ett problem måste lösa samma delproblem om och om igen, istället för att generera nya delproblem.

För att till exempel generera Fibonacci-serien kan denna rekursiva formulering övervägas: FN = F (N-1) + F (N-2), som tar ett grundläggande fall att F1 = F2 = 1. Då måste du: F33 = F32 + F31 och F32 = F31 + F30.

Som man kan se löses F31 i de rekursiva sub -mätningarna för både F33 och F32. Även om det totala antalet delproblem är riktigt litet, om en rekursiv lösning antas eftersom detta kommer att lösa samma problem om och om igen.

Kan tjäna dig: de sju komponenterna i ett informationssystem

Detta beaktas av dynamisk programmering, så det löser varje delproblem bara en gång. Detta kan uppnås på två sätt:

Toppmetod

Om lösningen på något problem kan formuleras rekursivt med hjälp av lösningen av sina underproblem, och om dessa delproblem överlappar varandra, kan lösningarna på delproblemen enkelt memoreras eller lagras i en tabell i en tabell.

Varje gång lösningen av ett nytt subproblema söks kommer den att granskas i tabellen om den tidigare har lösts. Om en lösning lagras kommer den att användas istället för att beräkna den igen. Annars kommer subproblema att lösas och lagra lösningen i tabellen.

Stigande tillvägagångssätt

Efter att lösningen av ett problem är rekursivt formulerat i termer av dess delproblem kan problemet prövas i en uppåt: först kommer de att försöka lösa delproblemen och använda sina lösningar för att nå lösningar till de största delproblemen.

Detta görs också vanligtvis i form av en tabell, vilket genererar iterativa lösningar till allt större delproblem genom att använda lösningar på små delproblem. Till exempel, om värdena på F31 och F30 redan är kända, kan värdet på F32 beräknas direkt.

Jämförelse med andra tekniker

Ett betydande tillhörighet av ett problem som kan lösas genom dynamisk programmering är att det borde ha överlappande delproblem. Detta är vad som skiljer den dynamiska programmeringen av tekniken för att dela och erövra, där det inte är nödvändigt att lagra de enklaste värdena.

Det liknar rekursion, eftersom genom att beräkna basfall kan det slutliga värdet bestämmas induktivt. Denna stigande metod fungerar bra när ett nytt värde beror endast på tidigare beräknade värden.

Exempel

Minsta steg för att nå 1

För alla positiva heltal "E" kan du utföra något av följande tre steg.

- Subtrahera 1 från numret. (E = E-1).

- Om det är delbart med 2, delas den med 2 (om e%2 == 0, då e = e/2).

- Om det är delbart med 3, delas den med 3 (om e%3 == 0, då e = e/3).

Baserat på de tidigare stegen måste du hitta minsta belopp av dessa steg att vidta och 1. Till exempel:

- Om E = 1, resultat: 0.

- Om E = 4, resultat: 2 (4/2 = 2/2 = 1).

- När E = 7, resultat: 3 (7-1 = 6/3 = 2/2 = 1).

Närma sig

Du kanske alltid tänker på att välja steget som gör n så lågt som möjligt och fortsätta så här tills den når 1. Det kan emellertid ses att denna strategi inte fungerar här.

Kan tjäna dig: kommersiell programvara

Till exempel, om E = 10, skulle stegen vara: 10/2 = 5-1 = 4/2 = 2/2 = 1 (4 steg). Det optimala sättet är dock: 10-1 = 9/3 = 3/3 = 1 (3 steg). Därför måste alla möjliga steg som kan göras för varje värde på n bevisas, vilket väljer minsta belopp av dessa möjligheter.

Allt börjar med rekursion: f (e) = 1 + min f (e-1), f (e/2), f (e/3) Om e> 1, tar som basfall: f (1 ) = 0. Med återfallsekvationen kan du börja koda rekursionen.

Det kan emellertid observeras att det har överlagrade delproblem. Dessutom beror den optimala lösningen för en given ingång på den optimala lösningen av dess delproblem.

Som i memorering, där lösningarna på de delproblem som löses lagras för att använda dem senare. Eller som i dynamisk programmering börjar det underifrån och går vidare till den givna E. Nästa, båda koderna:

Memorering

Dynamisk uppåt programmering

Fördelar

En av de viktigaste fördelarna med att använda dynamisk programmering är att den påskyndar bearbetning, eftersom referenser som tidigare beräknades är använd. Som en rekursiv programmeringsteknik reducerar det programkodlinjer.

Vorace Algoritmos vs dynamisk programmering

Vorecious algoritmer liknar dynamisk programmering i den meningen att båda är verktyg för optimering. Voraz -algoritmen söker dock en optimal lösning i varje lokalt steg. Det vill säga det söker ett girigt val med hopp om att hitta ett globalt optimalt.

Därför kan glupiga algoritmer göra ett antagande som ser optimalt ut vid den tiden, men som blir dyr i framtiden och garanterar inte en global optimal.

Å andra sidan hittar dynamisk programmering den optimala lösningen för delproblem och gör sedan ett informerat val genom att kombinera resultaten från dessa delproblem för att verkligen hitta den mest optimala lösningen.

Nackdelar

- Mycket minne behövs för att lagra det beräknade resultatet av varje delproblem, utan att kunna se till att det lagrade värdet kommer att användas eller inte.

- Många gånger lagras utgångsvärdet utan att någonsin användas i följande delproblem under körningen. Detta leder till onödig användning av minne.

- Vid dynamisk programmering kallas funktionerna rekursivt. Detta gör att batteriminnet förblir i ständig ökning.

Rekursivitet vs dynamisk programmering

Om du har begränsat minne för att utföra koden och bearbetningshastigheten inte är oroande, kan rekursivitet användas. Till exempel, om en mobilapplikation utvecklas är minnet mycket begränsat för att utföra applikationen.

Kan tjäna dig: blandade enheter: egenskaper och exempel

Om programmet önskas att utföras snabbare och det inte finns några minnesbegränsningar, är det att föredra att använda dynamisk programmering.

Ansökningar

Dynamisk programmering är en effektiv metod för att lösa problem som annars kan verka extremt svåra att lösa på rimlig tid.

Algoritmer baserade på det dynamiska programmeringsparadigmet används i många vetenskapsområden, inklusive många exempel på konstgjord intelligens, från upplösning av planeringsproblem till röstigenkänning.

Dynamiska programmeringsalgoritmer

Dynamisk programmering är ganska effektiv och tjänar mycket bra för ett brett utbud av problem. Många algoritmer kan ses som tillämpningar av glupiga algoritmer, till exempel:

- Fibonacci Numbers Series.

- Hanoi torn.

- Alla kortaste rutter parar av Floyd-Warshall.

- Ryggsäck.

- Projektprogrammering.

- Den kortaste vägen av Dijkstra.

- Robotikflygkontroll och kontroll.

- Matematiska optimeringsproblem.

- Delad tid: Programmera arbetet för att maximera användningen av CPU.

Fibonacci Numbers Series

Fibonacci -nummer är siffrorna som finns i följande sekvens: 0, 1, 1, 3, 5, 8, 13, 21, 34, 55, 89, 144, etc.

I matematisk terminologi definieras FN -följd av fibonacci -nummer av återfallsformeln: f (n) = f (n -1) + f (n -2), där f (0) = 0 och f (1) = 1.

Toppmetod

I det här exemplet initialiseras en sökmatris med alla initiala värden med -1. När lösningen på ett delproblem behövs kommer den först att sökas i denna sökmatris.

Om det finns det beräknade värdet kommer det värdet att returneras. Annars kommer resultatet att beräknas för att lagra det i sökmatrisen och därmed kunna återanvända den senare.

Stigande tillvägagångssätt

I det här fallet, för samma Fibonacci -serie, F (0), sedan F (1), F (2), F (3), och så vidare beräknas först. Således kommer lösningarna på delproblemen från botten att byggas.

Referenser

1. Vineet Choudhary (2020). Introduktion till dynamisk programmering. Orustersidare.Taget från: DeveloperInsider.co.
2. Alex Allain (2020). Dynamisk programmering i c++. C -programmering. Taget från: cprogrammming.com.
3. Efter akademin (2020). Idé om dynamisk programmering. Taget från: Afteracademy.com.
4. Aniruddha Chaudhari (2019). Dynamisk programmering och rekursion | Annorlunda. CSE -stack. Taget från: csestack.org.
5. Kodkock (2020). För dynamisk programmeringsstudie. Taget från: codhef.com.
6. Programiz (2020). Dynamisk programmering. Taget från: Programiz.com.