Linjär programmering Vad är det för, modeller, begränsningar, applikationer

De linjär programmering Det är en matematisk metod som tjänar till att optimera (maximera eller minimera efter behov) en funktion vars variabler är föremål för begränsningar, så länge funktionen och begränsningarna är linjärt beroende på variablerna.

Generellt sett är funktionen för att optimera en praktisk situation, till exempel förstärkningen av en tillverkare vars insatser, arbetskraft eller maskiner är begränsad.

Figur 1. Linjär programmering används ofta för att optimera vinsten. Källa: Piqsels.

Ett av de enklaste fallen är en linjär funktion för att maximera, vilket bara beror på två variabler, kallade Beslutsvariabler. Det kan vara form:

Z = k₁x + k₂och

Med k₁ och k₂ konstanter. Denna funktion är känd som Objektiv funktion. Naturligtvis finns det situationer som förtjänar mer än två variabler för sin studie, som är mer komplexa:

Z = k₁x₁ + k₂x₂ + k₃x₃ +.. .

Och begränsningar modelleras också matematiskt genom ett system med ekvationer eller ojämlikheter, lika linjära x och och.

Uppsättningen av lösningar i detta system kallas genomförbara lösningar antingen genomförbara poäng. Och bland de genomförbara punkterna finns det minst en, som optimerar objektivfunktionen.

Linjär programmering utvecklades oberoende av amerikansk fysiker och matematiker.

Problemlösningsmetoden känd som Simplexmetod Det är skapandet av Dantzig, som arbetade för US Air Force, University of Berkeley och Stanford University.

figur 2. Matematikerna George Dantzig (vänster) och Leonid Kantorovich (höger). Källa: f. Zapata.

[TOC]

Linjära programmeringsmodeller

De nödvändiga elementen för att skapa en linjär programmeringsmodell, som är lämplig för en praktisk situation, är:

-Objektiv funktion

-Beslutsvariabler

-Begränsningar

I objektivfunktionen definieras vad du vill uppnå. Anta till exempel att det är önskvärt att maximera de vinster som erhållits från tillverkning av vissa produkter. Då fastställs "vinst" -funktionen enligt det pris där produkterna säljs.

I matematiska termer kan denna funktion uttryckas förkortas med summering:

Z = ∑k_Yo x_Yo

I denna ekvation, k_Yo De är koefficienter och x_Yo är beslutsvariablerna.

Beslutsvariabler är elementen i systemet vars kontroll är och deras värden är positiva verkliga siffror. I det föreslagna exemplet är beslutsvariablerna mängden av varje produkt som ska tillverkas för att erhålla maximal förstärkning.

Slutligen har vi begränsningarna, som är linjära ekvationer eller ojämlikheter när det gäller beslutsvariablerna. De beskriver begränsningarna i problemet, som är kända och kan till exempel vara mängden råvaror som finns tillgängliga vid tillverkningen.

Kan tjäna dig: funktioner med högre än två (exempel)

Typer av begränsningar

Du kan ha ett belopp m begränsningar, från och med J = 1 fram tills J = m. Matematiskt är begränsningarna av tre typer:

1. TILL_J = ∑ a_{I j} . x_Yo
2. B_J ≥ ∑ b_{I j} . x_Yo
3. C_J ≤ ∑ c_{I j} . x_Yo

Den första begränsningen är av linjär ekvationstyp och innebär att värdet till_J, vilket är känt måste respekteras.

De återstående två begränsningarna är linjära ojämlikheter och innebär att B -värdena_J och C_J, Känd, kan respekteras eller övervinnas, när symbolen som visas är ≥ (större eller lika med) eller respekt eller inte övervinnas, om symbolen är ≤ (mindre än eller lika med).

Modellexempel

Tillämpningsområdet är mycket olika, som täcker från företagsekonomi till näring, men för att förstå metoden föreslås en enkel modell av en praktisk situation med två variabler.

Ett lokalt bakverk är känt för två specialiteter: den svarta djungelkakan och Sacrista -kakan.

I sin utarbetande kräver de ägg och socker. För den svarta djungeln behövs 9 ägg och 500 g socker, medan 8 ägg och 800 g socker är nödvändiga för Sacripenin. De respektive försäljningspriserna är $ 8 och 10.

Problemet är: hur många kakor av varje typ ska konditoriet göra för att maximera sin förstärkning, veta att den har 10 kilo socker och 144 ägg?

Beslutsvariabler

Beslutsvariablerna är "X" och "Y", som tar verkliga värden:

-X: Mängden svarta djungelkakor

-Y: Kakor av sakrifantin.

Begränsningar

Begränsningarna ges av det faktum att antalet kakor är en positiv mängd och det finns begränsade mängder råmaterial för att förbereda dem.

Därför förvärvar dessa begränsningar på matematiskt sätt:

1. x ≥ 0
2. och ≥0
3. 9x +8y ≤ 144
4. 0.5 x + 0.8 och ≤ 10

Begränsningarna 1 och 2 utgör Icke -negativitetsvillkor Tidigare exponerad, och alla införda ojämlikheter är linjära. I begränsningarna är 3 och 4 värden som inte bör övervinnas: 144 ägg och 10 kg socker.

Objektiv funktion

Slutligen är objektivfunktionen den förstärkning som erhålls genom att tillverka "x" mängden svarta djungelkakor plus "y" mängder sakristiner. Det är byggt multipliceringspris med mängd kakor som tillverkas och lägger till för varje typ. Det är en linjär funktion som vi kommer att kalla g (x, y):

G = 8x + 10y

Lösningsmetoder

Bland de olika lösningsmetoderna är grafiska metoder, Simplex -algoritmen och den inre punktmetoden, för att nämna vissa.

- Grafisk eller geometrisk metod

När du har problem med två variabler som föregående avsnitt bestämmer begränsningarna en polygonal region i planet Xy, ring upp genomförbar region antingen Livskraftsregion.

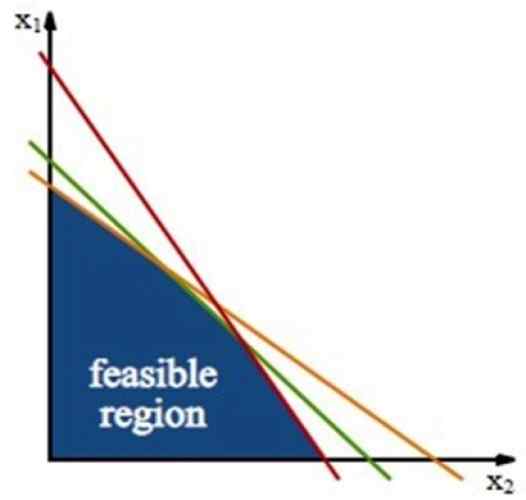Figur 3. Den genomförbara regionen, där lösningen av optimeringsproblemet finns. Källa: Wikimedia Commons.

Denna region är byggd genom Restriktionslinjer, som är de linjer som erhålls från ojämlikheterna i begränsningarna och arbetar endast med tecken på jämlikhet.

Kan tjäna dig: Finite Set: Egenskaper, exempel, lösta övningar

När det gäller bageri som vill optimera vinsten är begränsningslinjer:

1. x = 0
2. y = 0
3. 9x +8y = 144
4. 0.5 x + 0.8y = 10

Alla punkter i regionen som låsts av dessa linjer är möjliga lösningar, så det finns oändliga av dem. Förutom i det fall det genomförbara regionen är tomt, i vilket fall problemet saknar en lösning.

Lyckligtvis, för konditoriet.

Figur 4. Det genomförbara regionen för konditoriet. Den raka linjen 0 korsar ursprunget. Källa: f. Zapata med geogebra.

Den optimala lösningen, om den finns, är med hjälp av objektivfunktionen. Till exempel, när det gäller att hitta den maximala G -förstärkningen, har du följande rad, som kallas Iso-nackdelar rak:

G = k₁x + k₂och → y = -k₁x / k₂ + G/ k₂

Med denna linje erhålls alla par (x, y) som ger en given förstärkning g, så det finns en familj av linjer beroende på värdet på g, men alla med samma lutning -k₁ / k₂, så att de är parallella raka.

Den optimala lösningen

Nu kan det demonstreras att den optimala lösningen av ett linjärt problem alltid är ett extremt eller toppunkt i det genomförbara regionen. Så:

Linjelösningen är längst från ursprunget och som har åtminstone en punkt gemensamt med det genomförbara regionen.

Om linjen som är närmast ursprunget har ett helt segment gemensamt med det genomförbara regionen, sägs det att det finns oändliga lösningar. Detta fall inträffar om lutningen för iso-fördelarna är lika med den för någon av de andra linjerna som begränsar regionen.

För vår konditorivaror är kandidatens vertikaler A, B och C.

- Simplex Method of Dantzig

Den grafiska eller geometriska metoden är tillämplig för två variabler. Det är emellertid mer komplicerat när det finns tre variabler och omöjligt att använda för ett större antal variabler.

När det gäller problem med mer än två variabler, Simplexmetod, som består av en serie algoritmer för att optimera objektiva funktioner. Enkla matriser och aritmetik används vanligtvis för att utföra beräkningarna.

Simplex -metoden börjar med att välja en genomförbar lösning och kontrollera om den är optimal. Om det är har vi redan löst problemet, men om det inte är det fortsätter det mot en lösning närmare optimering. Om lösningen finns, algoritmen med den i några försök.

Kan tjäna dig: vad är statistikområdet? (Med exempel)

Ansökningar

Linjär och icke-linjär programmering tillämpas på många områden för att fatta de bästa besluten för att minska kostnaderna och öka vinsten, som inte alltid är monetära, eftersom de kan mätas i tid, till exempel om du försöker minimera den nödvändiga tiden att genomföra den en serie operationer.

Här är några fält:

-I marknadsföring används det för att hitta den bästa kombinationen av media (sociala nätverk, tv, press och andra) för att annonsera en viss produkt.

-För tilldelning av arbete som är lämpligt för personalen för ett företag eller fabrik eller scheman till dem.

-Vid valet av den mest näringsrika maten och till lägsta kostnad i boskap och fjäderfäindustri.

Löst övningar

- Övning 1

Graf den linjära programmeringsmodellen som tas upp i föregående avsnitt.

Lösning

Det är nödvändigt att grafera uppsättningen av värden som bestäms av systemet med begränsningar som anges i problemet:

1. x ≥ 0
2. och ≥0
3. 9x +8y ≤ 144
4. 0.5 x + 0.8 och ≤ 10

Regionen som ges av ojämlikheterna 1 och 2 motsvarar den första kvadranten i det kartesiska planet. När det gäller ojämlikheter 3 och 4 börjar det med att hitta begränsningslinjerna:

9x +8y = 144

0.5 x + 0.8y = 10 → 5x + 8y = 100

Det genomförbara området är en fyrkantig vars toppar är punkter a, b, c och d.

Minsta förstärkning är 0, därför är 8x + 10 och 10 -linjen den nedre gränsen och de iso -förenliga linjerna har väntat -8/10 = -0.8.

Detta värde skiljer sig från sluttningarna för de andra begränsningslinjerna och eftersom det genomförbara området är begränsat, finns det den unika lösningen.

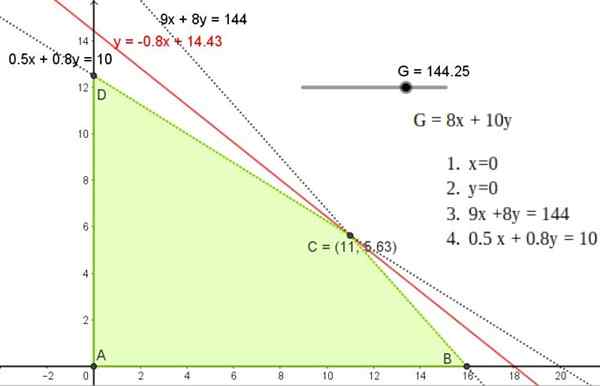Figur 5. Grafisk lösning av övning 1, som visar det genomförbara området och punktlösningen C i en av vertikalerna i nämnda region. Källa: f. Zapata.

Denna lösning motsvarar en lutningslinje -0.8 som passerar genom en av punkterna A, B eller C, vars koordinater är:

A (11; 5.625)

B (0; 12.5)

C (16, 0)

Optimal lösning

Vi beräknar värdet på G för var och en av dessa punkter:

-(11; 5.625): g_TILL = 8 x 11 + 10 x 5.625 = 144.25

-(0; 12.5): g_B = 8 x 0 + 10 x 12.5 = 125

-(16, 0): g_C = 8 x 16 + 10 x 0 = 128

Den största vinsten är att tillverka 11 svarta djungelkakor och 5.625 sakripantinska kakor. Denna lösning överensstämmer med den som hittades genom programvaran.

- Övning 2

Kontrollera resultatet av den tidigare övningen genom att använda den tillgängliga lösaren (Solutioner) i de flesta kalkylblad som Excel eller Calc de LibreOffice, som innehåller Simplex -algoritmen för linjär programmeringsoptimering.

Lösning

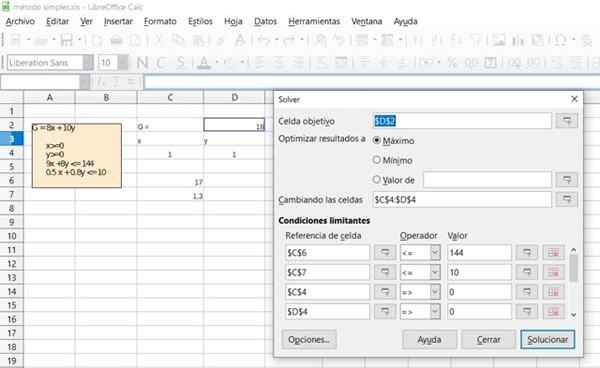Figur 6. Detalj av lösningen av övning 1 genom det gratis Office Calc -kalkylbladet. Källa: f. Zapata. 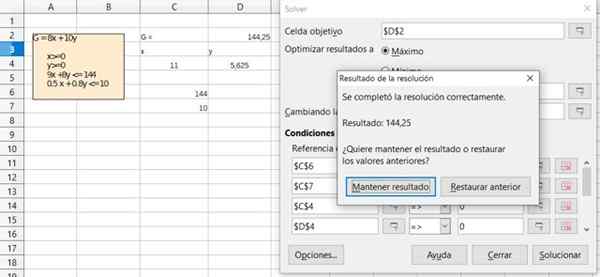Figur 7. Detalj av lösningen av övning 1 genom det gratis Office Calc -kalkylbladet. Källa: f. Zapata.

Referenser

1. Lysande. Linjär programmering. Återhämtat sig från: lysande.org.
2. Eppen, g. 2000. Operationsforskning inom administrativ vetenskap. Femte. Utgåva. Prentice hall.
3. Haeussler, E. 1992. Matematik för administration och ekonomi. 2: a. Utgåva. Ibero -amerikansk redaktionsgrupp.
4. Hiru.Eus. Linjär programmering. Återhämtat sig från: hiru.Eus.
5. Wikipedia. Linjär programmering. Återhämtad från: är. Wikipedia.org.