Fastighetsfastigheter, exempel

De Algebra låsegenskap Det är ett fenomen som relaterar två delar av en uppsättning med en operation, där det nödvändiga villkoret är att resultatet, efter de två elementen under nämnda operation, också tillhör den första uppsättningen.

Till exempel, om jämna siffror tas som helhet och en summa som en operation, erhålls ett lås av nämnda uppsättning med avseende på summan. Detta beror på att summan av 2 jämna siffror alltid kommer att ges som ett resultat ett annat nummer, vilket uppfyller låsvillkoret.

Källa: Unspash.com

[TOC]

Egenskaper

Det finns många egenskaper som bestämmer algebraiska utrymmen eller kroppar, till exempel strukturer eller ringar. Låsegenskap är emellertid en av de mest kända inom den grundläggande algebra.

Inte alla tillämpningar av dessa egenskaper är baserade på fenomen eller numeriska element. Många vardagliga exempel kan arbeta från en algebraisk teoretisk strategi ren.

Ett exempel kan vara medborgarna i ett land som antar ett juridiskt förhållande av något slag, till exempel kommersiellt eller äktenskapssamhället. Efter denna operation eller ledning är de fortfarande medborgare i landet. Således representerar medborgarskap och ledningsoperationer med avseende på två medborgare ett lås.

Numerisk algebra

När det gäller siffror finns det många aspekter som har varit en anledning till studier i olika matematikströmmar och algebra. Från dessa studier har ett stort antal axiomer och teorier framkommit som fungerar som teoretisk grund för samtida forskning och verk.

Om du arbetar med numeriska uppsättningar kan vi fastställa en annan giltig definition för låsegenskaper. Det sägs att en uppsättning A är låset i en annan uppsättning B om A är den minsta uppsättningen som innehåller alla uppsättningar och operationer som hus B.

Kan tjäna dig: distribuerande egendom

Demonstration

Låsdemonstration tillämpas på element och operationer som finns i uppsättningen verkliga n -nummer.

Låt A och B vara två siffror som tillhör uppsättningen R, är låset för dessa element definierat för varje operation som finns i R.

Tillägg

- Sum: ∀ A ˄ B ∈ R → A + B = C ∈ R

Detta är det algebraiska sättet att säga det För alla A och B som tillhör verkliga siffror måste det vara summan av en mer B är lika med C, vilket också tillhör det verkliga.

Det är lätt att kontrollera om detta förslag är sant; Det räcker för att göra summan mellan något verkligt nummer och verifiera om resultatet också tillhör de verkliga siffrorna.

3 + 2 = 5 ∈ R

-2 + (-7) = -9 ∈ R

-3 + 1/3 = -8/3 ∈ R

5/2 + (-2/3) = 11/6 ∈ R

Det observeras att låstillståndet uppfylls för verkliga siffror och summan. På detta sätt kan det avslutas: Summan av verkliga siffror är ett algebraiskt lås.

Multiplikation

- Multiplikation: ∀ A ˄ B ∈ R → A . B = c ∈ R

För alla A och B som tillhör de riktiga är multiplikationen av A för B lika med C, som också tillhör det verkliga.

Vid verifiering med samma element i föregående exempel observeras följande resultat.

3 x 2 = 6 ∈ R

-2 x (-7) = 14 ∈ R

-3 x 1/3 = -1 ∈ R

5/2 x (-2/3) = -5/3 ∈ R

Detta är tillräckligt bevis för att dra slutsatsen att: Multiplikationen av verkliga siffror är ett algebraiskt lås.

Denna definition kan utvidgas till alla verkliga siffror, även om vi hittar vissa undantag.

Källa: Pixabay.com

Särskilda fall i R

Division

Som ett speciellt fall observeras divisionen, där följande undantag uppskattas:

Kan tjäna dig: klassisk sannolikhet: beräkning, exempel, lösta övningar

∀ A ˄ B ∈ R → A / B ∉ R ↔ B = 0

För alla A och B som tillhör R Det måste mellan B inte tillhör reais om och bara om B är lika med noll.

Detta fall hänvisar till begränsningen av att inte kunna dela mellan noll. Eftersom noll tillhör de verkliga siffrorna dras det slutsatsen att: lDivision är inte ett lås i det verkliga.

Radio

Det finns också potentieringsoperationer, mer specifikt de för arkivering, där undantag presenteras för radikala momentindex:

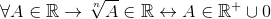; Med n par

För allt som det tillhör det kungliga.

På detta sätt betecknas det att de jämna rötterna endast gäller de positiva riktiga och det dras slutsatsen att förstärkningen inte är ett lås i R.

Logaritm

Det är godkänt för den logaritmiska funktionen, som inte är definierad för värden mindre eller lika med noll. För att kontrollera om logaritmen är ett R -lås fortsätter enligt följande:

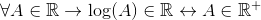
För allt som det tillhör reais tillhör logaritmen för reais, om och bara om det tillhör den positiva verkliga.

När de negativa och nollvärdena som också tillhör r utesluts kan det bekräftas att:

Logaritm är inte ett lås av riktiga siffror.

Exempel

Kontrollera låset för summan och subtraktionen av naturliga siffror:

Summan i n

Det första är att kontrollera låsvillkoret för olika element i den givna uppsättningen, där om det observeras att vissa element bryter med tillståndet, kan förekomsten av lås automatiskt förnekas.

Kan tjäna dig: konvergensradio: definition, exempel och övningar löst

Den här egenskapen uppfylls för alla möjliga värden på A och B, som observerats i följande operationer:

1 + 3 = 4 ∈ N

5 + 7 = 12 ∈ N

1000 + 10000 = 11000 ∈ N

Det finns inga naturliga värden som bryter låstillståndet, så det dras slutsatsen:

Summan är ett lås i N.

Subtrakt i n

Naturliga element söks kapabla att bryta tillståndet; A - B tillhör de infödda.

Drift Det är lätt att hitta par av naturliga element som inte uppfyller låsvillkoret. Till exempel:

7 - 10 = -3 ∉ A N

På så sätt kan vi dra slutsatsen att:

Subtraktionen är inte ett lås i uppsättningen av naturliga siffror.

Föreslagna övningar

1-samp.

2-Förslöjande om uppsättningen av verkliga siffror är ett lås av hela siffrorna.

3-bestämmare vilken numerisk uppsättning kan vara det verkliga siffrorna.

4-prov låsegenskapen för uppsättningen av imaginära nummer, med avseende på summan, subtraktion, multiplikation och uppdelning.

Referenser

1. Panorama of Pure Mathematics: The Bourbakist Choice. Jean dieudonné. Reverte, 1987.
2. Algebraiska siffror. Alejandro J. Díaz Barriga, Ana Irene Ramírez, Francisco Tomás. National Autonomous University of Mexico, 1975.
3. Linjär algebra och dess applikationer. Sandra Ibeth Ochoa García, Eduardo Gutiérrez González.
4. Algebraiska strukturer V: Kroppsteori. Héctor a. Merklen. Organisation av amerikanska stater, generalsekretariat, 1979.
5. Introduktion till kommutativ algebra. Michael Francis Atiyah, i. G. Macdonald. Reverte, 1973.