Radikala egenskaper

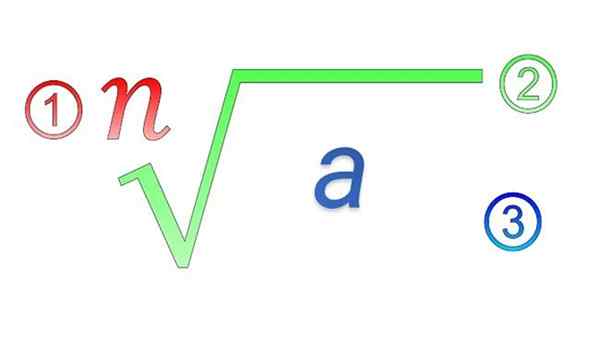
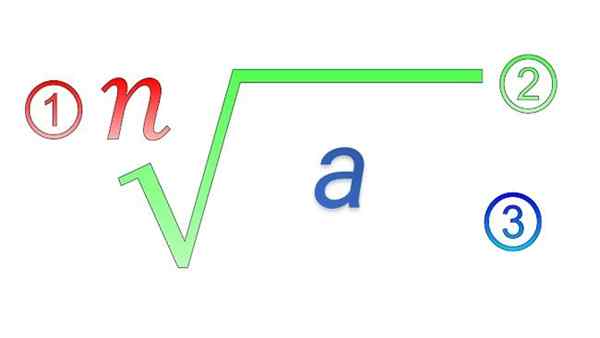Radikala element: 1) index; 2) radikal symbol; 3) subradisk mängd

Vilka är radikalens egenskaper?

De radikala egenskaper De är operationer som tillåter att lösa komplexa problem med radikaler och krafter. Radikalen är sättet att symbolisera matematiskt till N-EME för ett belopp "A". Denna rot är en annan mängd, kallad "B", så att namnet är exakt "A", så det är giltigt att skriva följande:

Värdet på "n" är ett naturligt tal, som kallas rotindexet, "a" är den Radikerande eller subradisk mängd, och "B" är N-EME för "en" rot. Både "A" och "B" tillhör uppsättningen verkliga siffror.

Om indexet inte är skrivet i en radikal förstås det omedelbart att dess värde är lika med 2 och läser "kvadratrot av en".

Eftersom "n" tillhör uppsättningen av naturliga nummer kan det vara ett par eller udda nummer. Sedan kännetecknas följande fall:

För "n" par

• Om A> 0 eller lika med 0 är den n-alkal roten till "A" positiv eller 0 och kallas huvudrot.
• När man < 0, no existe raíz n-ésima en el conjunto de los números reales, pero sí en los números complejos.

För “n” udda

• Ja a> 0, n-me för "a" roten är positiv.
• När man< 0, la raíz n-ésima de “a” es negativa.

Några exempel är följande:

Filmegenskaper

Det är möjligt att skriva namnet på ett belopp som en kraft med fraktionerad exponent, det vill säga ett rationellt antal.

I detta fall blir rotindex nämnaren, medan exponenten för den subradiska mängden blir teller:

Kan tjäna dig: Homografisk funktion: Hur man graferar, löste övningar

Uttryck som är giltig så länge som n ≠ 0, eftersom inga fraktioner med en nämnaren antas.

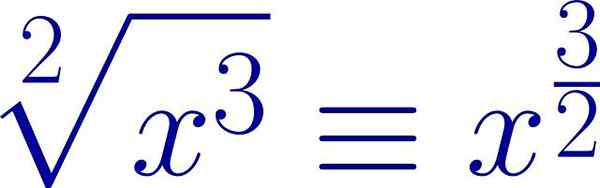Exempel på ett radikalt uttryck skrivet i form av en fraktionerad exponent. Rotindexet är exponentens nämnaren, medan sändarens kraft är telleren. Källa: Wikimedia Commons.

På detta sätt kan samma egenskaper som gäller för krafterna användas vid radikaler.

För värden som tillhör uppsättningen av verkliga siffror är dessa egenskaper följande:

1. Radikal produkt med lika index

I produkten av två (eller fler) radikaler med samma index multipliceras de subradiska mängderna, vilket bibehåller indexet:

2. Radikal kvot för samma index

Kvoten mellan n-that roten till "A" och N-EME för "B", som är B ≠ 0, är ​​lika med den N-emeasy roten till kvoten mellan "A" och "B":

3. Rotrot

För att hitta den n-emeasy roten till m-eMe för mängden "a", skrivs det subradiska beloppet under en rot vars index är produkten mellan "n" och "m":

Förfarandet utvidgas enkelt till successiva kapslade rötter. Det resulterande rotindexet är produkten från alla index, så här:

4. Rotkraft

En n-that, höjd till kraften M, uttrycker det subradiska beloppet till nämnda makt:

Särskilda fall:

1) Ja n = m, Rotskylten försvinner och lämnar basen upphöjd till kraft 1:

Som är giltigt för ≥ 0. I allmänhet, om rotindexet är ett jämnt nummer, har du:

(Se exempel senare)

2) Ja m> n, M/N -fraktionen är olämplig och roten kan förenklas, till exempel, leta efter fraktionen som motsvarar M/N så att telleren och nämnaren är kusiner med varandra, eller skriver om subradical mängden och tillämpar en del av de Egenskaper som beskrivs här.

Kan tjäna dig: prismor och pyramider

(Se exempel senare)

5. Radikalförstärkning

En radikal kan förstärkas med en faktor q, Om både rotindexet, såväl som kraften i den subradiska mängden, multiplicerar med nämnda faktor, och denna operation innebär inte modifieringen av resultatet. Därför:

Under förutsättning att ≥ 0 när det är jämnt.

6. Introduktion av en faktor inom en radikal

Om en positiv "B" -faktor multiplicerar en radikal kan den passera inom den, om den stiger till samma rotindex. Isåfall:

7. Summa och subtraktion av radikaler

Radikalerna kan lägga till och subtrahera, så länge de är samma index och har samma subradiska mängd.

När två eller flera radikala är av lika index och subradisk mängd, sägs det att de är Liknande radikaler.

Till exempel är följande radikaler liknande:

Istället är dessa radikaler inte lika, eftersom de inte har samma subradiska mängd:

Dessa två liknar inte heller:

Eftersom det radikala indexet inte är detsamma.

Liknande radikaler kan reduceras till en, lägga till eller subtrahera koefficienterna som följer med dem.

Exempel på radikala egenskaper

Exempel 1

Vad är värdet på följande rötter?

Den kvadratiska roten på 32 finns direkt med hjälp av räknaren. Dess värde är:

De hängande punkterna indikerar att det finns oändligt decimal.

Om du föredrar att inte arbeta med decimalnummer kan kvadratroten på 32 också beräknas genom att sönderdela 32 i sina främsta faktorer:

32 = 2⁵

På detta sätt, vid ersättning, erhålls det:

Kan tjäna dig: delare av 8: vad är och enkel förklaring

Skrivet som en fraktionerad exponent:

Fraktion 5/2 är olämplig, så att radikalen kan förenklas med hjälp av krafternas egenskaper:

Nu tillämpa egendom 1 ovan:

Därför:

För sin del:

Sedan (−2)³ = −8.

Enligt egendom 4:

Och slutligen finns den kvadratroten av −8 inte i uppsättningen av verkliga siffror, även om det är i de komplexa siffrorna.

Exempel 2

Med tanke på följande operation:

Är det möjligt att minska resultatet?

Förutsatt att radikalerna är liknande är det möjligt att minska dem, men för detta måste de ha samma index och samma subradisk mängd. I det föregående exemplet sågs man att:

En analog procedur kan användas för att skriva den första tillägget, så att den subradiska mängden är lika med 2:

Denna radikal liknar den föregående. När det gäller kvadratroten 81 är detta 9, därför:

Exempel 3

Vilka egenskaper är nödvändiga för att tillämpa för att utföra denna operation?

Vi måste tillämpa egenskaper 3 respektive 5, som är roten till en rot och introduktion av ett radikalt värde. Först gäller Property 5 för att introducera "X" som ligger utanför den innersta roten:

Och nu är uttrycket redo att tillämpa egendom 3 och multiplicera respektive index för varje radikal:

Referenser

1. Gonzales, D. 2011. Grundalgebra: teori och praktik. 2: a. Utgåva.
2. Haeussler, E. 2012. Förkalkning. Första. Utgåva. Pearson.
3. Khan acadaem. Exponenter och radikaler. Återhämtat sig från: Khanacademy.org.
4. Larson, r. 2012. Förkalkning. 8th. Utgåva. Cengage Learning.
5. Stewart, J. 2007. Matematik för beräkning. Femte. Utgåva. Cengage Learning.