Vad är akustisk impedans? Applikationer och övningar

De akustisk impedans o Specifik akustisk impedans är motståndet hos materiella medel för att passera ljudvågor. Det är konstant för ett visst medium, som går från ett stenigt skikt inuti jorden till den biologiska vävnaden.

Betecknar som z akustisk impedans, på matematiskt sätt måste det:

Z = ρ.v

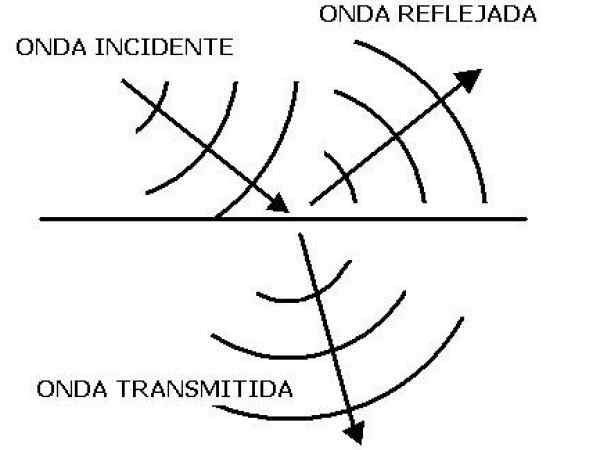
Figur 1. När en ljudvåg påverkar gränsen på två olika medel återspeglas en del och en annan överförs. Källa: Wikimedia Commons. Cristobal Aeorum/CC BY-SA (https: // Creativecommons.Org/licenser/BY-SA/4.0)

Där ρ är densitet och v hastigheten på ljudet från mediet. Detta uttryck är giltigt för en platt våg genom att röra sig i en vätska.

I enheter i det internationella systemet kommer densiteten i kg/m³ och hastigheten i m/s. Därför är enheterna för akustisk impedans kg/m².s.

På samma sätt definieras akustisk impedans som kvoten mellan tryck P och hastighet:

Z = p/v

Uttryckt på detta sätt är Z analogt med elektrisk motstånd R = V/I, där trycket representerar spänningspapperet och hastigheten för strömmen. Andra z -enheter om de skulle vara PA.s /m o n.EDER³, helt motsvarande de tidigare givna.

[TOC]

Överföring och reflektion av ljudvågen

När du har två olika medel för impedanser z₁ och z₂, En del av en ljudvåg som påverkar gränssnittet för båda kan överföras och en annan del kan återspeglas. Denna reflekterade eller Echo Wave är den som innehåller viktig information om det andra mediet.

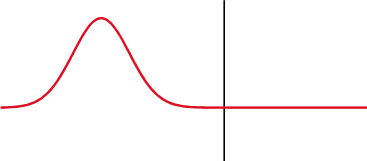figur 2. Incidentpuls, pulsöverförd och puls reflekteras. Källa: Wikimedia Commons.

Det sätt på vilket energin som transporteras av vågen distribueras beror på reflektionskoefficienterna r och T -överföring, två mycket användbara mängder för att studera spridningen av ljudvågen. För reflektionskoefficienten är kvoten:

R = i_r /Yo_antingen

Där jag_antingen Det är intensiteten i infallsvågen_r Det är intensiteten hos den reflekterade vågen. På liknande sätt har du transmissionskoefficienten:

T = i_t / Yo_antingen

Nu kan det demonstreras att intensiteten hos en platt våg är proportionell mot dess bredd till:

Det kan tjäna dig: durometer: Vad är det för, hur fungerar, delar, typer

I = (1/2) z.Ω² .TILL²

Där z är den akustiska impedansen för mediet och ω är vågens frekvens. Å andra sidan är förhållandet mellan den överförda amplituden och den infallande amplituden:

TILL_t/TILL_antingen = 2Z₁/(Z₁ +Z₂)

Som tillåter kvoten och_t /Yo_antingen  Det uttrycks i termer av amplituderna för infallande vågor och överföras som:

Yo_t /Yo_antingen = Z₂TILL_t² / Z₁TILL_antingen²

Genom dessa uttryck erhålls r och t i termer av akustisk impedans z.

Överföring och reflektionskoefficienter

Den främre kvoten är just överföringskoefficienten:

T = (z₂/Z₁) [2.Z₁/(Z₁ +Z₂)]]² = 4Z₁Z₂ /(Z₁ +Z₂)²

Eftersom förluster inte övervägs uppfylls det att incidentintensiteten är summan av den överförda intensiteten och den reflekterade intensiteten:

Yo_antingen = Jag_r + Yo_t → (i_r / Yo_antingen) + (I_t / Yo_antingen) = 1

Detta gör att vi kan hitta ett uttryck för reflektionskoefficienten när det gäller impedanserna för de två medierna:

R + t = 1 → r = 1 - t

Genom att utföra lite algebra för att ordna om termerna, reflektionskoefficienten är:

R = 1 - 4Z₁Z₂ /(Z₁ +Z₂)² = (Z₁ - Z₂)²/(Z₁ +Z₂)²

Och som i den reflekterade pulsen är informationen relaterad till det andra mediet, är reflektionskoefficienten av stort intresse.

Således, när de två medierna har en stor skillnad i impedans, blir telleren för det tidigare uttrycket större. Då är intensiteten hos den reflekterade vågen hög och innehåller bra information om mediet.

När det gäller den del av vågen som överförs till det andra mediet, dämpas det gradvis och energin sprids som värme.

Applikationer och övningar

Överförings- och reflektionsfenomen ger upphov till olika mycket viktiga tillämpningar, till exempel den sonar som utvecklats under andra världskriget och det tjänar till att upptäcka föremål. Förresten, vissa däggdjur som fladdermöss och delfiner har ett byggt -i sonarsystem.

Dessa egenskaper används också i stor utsträckning för att studera jordens inre i de seismiska prospekteringsmetoderna, för att erhålla medicinska bilder med ultraljud, mätning av bentäthet och ta bilder av olika strukturer på jakt efter misslyckanden och defekter.

Kan tjäna dig: Thomson Atomic Model: Egenskaper, postulat, subatomiska partiklar

Akustisk impedans är också en viktig parameter vid utvärdering av ljudresponsen hos ett musikinstrument.

- Motion Löst 1

Ultraljudstekniken för att få biologiska vävnadsbilder använder sig av högfrekvensljudpulser. Ekon innehåller information om organ och vävnader som går igenom, den programvaran är ansvarig för att översätta till en bild.

En ultraljudspuls påverkas till fettmusculusgränssnittet. Hitta: Hitta:

a) Den akustiska impedansen för varje tyg.

b) Procentandelen ultraljud återspeglas i gränssnittet mellan fett och muskler.

Fett

• Densitet: 952 kg/m³
• Ljudhastighet: 1450 m/s

Muskel

• Densitet: 1075 kg/m³
• Ljudhastighet: 1590 m/s

Lösning till

Den akustiska impedansen för varje vävnad ersätter i formeln:

Z = ρ.v

Den här vägen:

Z_fett = 952 kg/m³ x 1450 m/s = 1.38 x 10⁶ kg/m².s

Z_muskel = 1075 kg/m³ x 1590 m/s = 1.71 x 10⁶  kg/m².s

Lösning B

För att hitta procentandelen intensitet som återspeglas i gränssnittet mellan de två vävnaderna, reflektionskoefficienten som ges av:

R = (z₁ - Z₂)²/(Z₁ +Z₂)²

Här z_fett = Z₁ och z_muskel = Z_2. Reflektionskoefficienten är en positiv mängd, vilket garanteras av rutorna i ekvationen.

Ersätta och utvärdera:

R = (1.38 x 10⁶ - 1.71 x 10⁶ )²  / (1.38 x 10⁶ + 1.71 x 10⁶ )² = 0.0114.

Genom att multiplicera med 100 kommer vi att ha den reflekterade procentandelen: 1.14 % av incidentens intensitet.

- Motion Löst 2

En ljudvåg har en intensitetsnivå 100 decibel och påverkar normalt vattenytan. Bestäm intensitetsnivån för den överförda vågen och den för den reflekterade vågen.

Kan tjäna dig: Viskös friktion (kraft): koefficient och exempel

Data:

Vatten

• Densitet: 1000 kg/m³
• Ljudhastighet: 1430 m/s

Luft

• Densitet: 1.3 kg/m³
• Ljudhastighet: 330 m/s

Lösning

Nivån på decibels intensitet för en ljudvåg betecknas som l, är dimensionslös och ges av formeln:

L = 10 log (i /10^-12)

Höjning vid 10 på båda sidor:

10 ^L/10 = I /10^-12

Som L = 100 resulterar i:

I/10^-12 = 10¹⁰

Intensitetsenheterna ges när det gäller kraft per yta. I det internationella systemet är de watt/m². Därför är intensiteten hos den infallande vågen:

Yo_antingen = 10¹⁰ . 10^-12 = 0.01 w/m².

För att hitta intensiteten hos den överförda vågen beräknas överföringskoefficienten och multipliceras sedan med infallsintensiteten.

De respektive impedanserna är:

Z_vatten = 1000 kg/m³ x 1430 m/s = 1.43 x 10⁶ kg/m².s

Z_luft = 1.3 kg/m³ x 330 m/s = 429 kg/m².s

Ersätta och utvärdera i:

T = 4z₁Z₂ /(Z₁ +Z₂)² = 4 × 1.43 x 10⁶ X 429 / (1.43 x 10⁶ + 429)² = 1.12 x 10^-3

Så intensiteten hos den överförda vågen är:

Yo_t = 1.12 x 10^-3 x 0.01 w/m² = 1.12 x 10^-5 W/m²

Dess decibels intensitetsnivå beräknas av:

L_t = 10 log (i_t /10^-12) = 10 log (1.12 x 10^-5 / 10^-12) = 70.3 dB

För sin del är reflektionskoefficienten:

R = 1 - t = 0.99888

Med detta är intensiteten hos den reflekterade vågen:

Yo_r = 0.99888 x 0.01 w/m² = 9.99 x 10^-3 W/m²

Och dess intensitetsnivå är:

L_t = 10 log (i_r /10^-12) = 10 log (9.99 x 10^-3 / 10^-12) = 100 dB

Referenser

1. Andriessen, m. 2003. HSC Physics Course. Jacaranda.
2. Baranek, L. 1969. Akustik. Andra upplagan. Amerikanska latinamerikanska redaktion.
3. Kinsler, L. 2000. Grundläggande akustik. Wiley och söner.
4. Lowrie, w. 2007. Grundläggande geofysik. 2: a. Utgåva. Cambridge University Press.
5. Wikipedia. AKUSTISK IMPEDANS. Hämtad från: i.Wikipedia.org.