Vad är linjär hastighet? (Med lösta övningar)

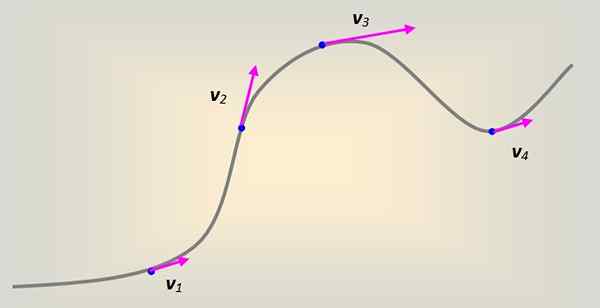
De Linjär hastighet Det definieras som det som alltid är tangentiellt för banan följt av partikeln, oavsett. Om partikeln alltid rör sig i en rätlinjig bana finns det inga problem att föreställa sig hur hastighetsvektorn åtföljer denna raka linje.

Men i allmänhet genomförs rörelsen på en kurva godtyckligt. Varje del av kurvan kan modelleras som om den var en del av en radiocirkel till, som vid varje punkt är tangent till den följda vägen.

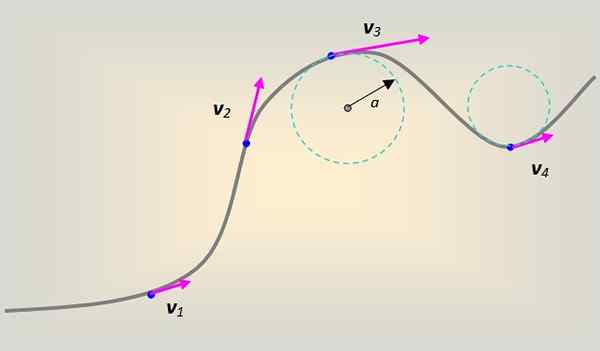Figur 1. Linjär hastighet på en mobil som beskriver en kröklig bana. Källa: Självgjord.

I detta fall åtföljer den linjära hastigheten tangentiellt och hela tiden till kurvan vid varje punkt av den.

Matematiskt omedelbar linjär hastighet är derivatet av positionen med avseende på tid. Vara r partikelens positionsvektor på ett ögonblick t, Sedan ges den linjära hastigheten av uttrycket:

v = r'(T) = Dr / dt

Detta innebär att linjär hastighet eller tangentiell hastighet, som den också kallas, är inget annat än förändringen av positionen med avseende på tid.

[TOC]

Linjär hastighet i cirkulär rörelse

När rörelsen är på en omkrets kan vi gå bredvid partikeln vid varje punkt och se vad som händer i två mycket speciella riktningar: en av dem är den som alltid pekar på centrum. Detta är adressen radiell.

Den andra viktiga riktningen är den som äger rum på omkretsen, detta är adressen tangentiell Och den linjära hastigheten har det alltid.

Kan tjäna dig: manometriskt tryck: förklaring, formler, ekvationer, exempel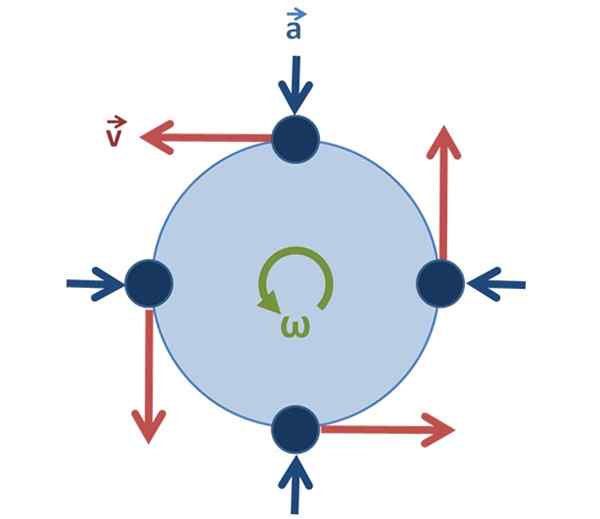figur 2. Enhetlig cirkulär rörelse: Hastighetsvektorn ändrar riktning och riktning när partikeln roterar, men dess storlek är densamma. Källa: Original av användare: BREWS_OHARE, SVGED av användare: SJLEGG [CC BY-SA 3.0 (https: // CreativeCommons.Org/licenser/BY-SA/3.0)].

När det gäller den enhetliga cirkulära rörelsen är det viktigt ja det förblir oförändrat.

För denna rörelse ges positionen som en funktion av tiden av S (t), var s Är han Båge och t Det är dags. I så fall ges den omedelbara hastigheten av uttrycket V = ds/dt Och det är konstant.

Om hastighetens storlek också varierar (vi vet redan att riktningen alltid gör det, annars kunde mobilen inte vända), vi står inför en varierad cirkulär rörelse, under vilken mobil utöver att rotera, den kan stoppa eller accelerera.

Linjär hastighet, vinkelhastighet och centripetalacceleration

Partikelrörelsen kan också ses med tanke på svepningsvinkel, Istället för att göra det från det reste målet. I det här fallet talas det om vinkelhastighet. För en rörelse på en radiocirkel R, Det finns en relation mellan bågen (i radianer) och vinkeln:

S = r θ

Härleda med avseende på båda sidor:

ds/dt = r (dθ/dt)

Kallar derivatet av θ med avseende på t som vinkelhastighet Och betecknar det med den grekiska bokstaven ω "Omega", du har det här förhållandet:

v = ωR

Centripetalacceleration

Varje cirkulär rörelse har centripetalacceleration, som alltid riktas mot omkretsens centrum. Hon tar hand om att hastigheten förändras för att röra sig med partikeln när den vänder.

Det kan tjäna dig: kalibreringskurva: vad är det för, hur man gör det, exempel

Centripetalacceleration till_c antingen till_R Det pekar alltid på mitten (se figur 2) och är relaterad till den linjära hastigheten på detta sätt:

till_c = v² /R

Och med vinkelhastighet som:

till_c = (ΩR)² /R = Ω²R

För en enhetlig cirkulär rörelse, positionen S (t) Det är av formen:

S (t) = så+ vt

Dessutom måste den olika cirkulära rörelsen ha en del av accelerationen som heter Tangentiell acceleration till_T, som handlar om att ändra storleken på linjär hastighet. Ja till_T  det är konstant, Positionen är:

S (t) = s_antingen + v_antingenT + ½ a_Tt²

Med v_antingen Som den första hastigheten.

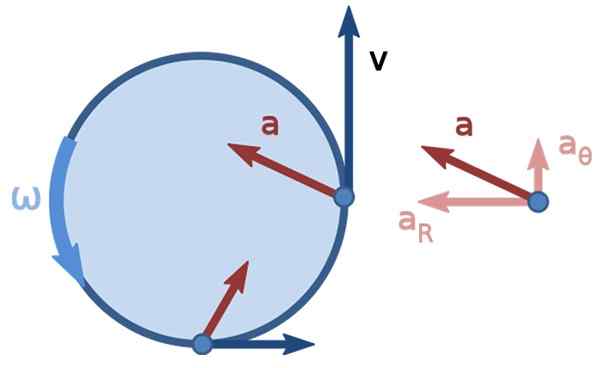Figur 3. Icke -enhetlig cirkulär rörelse. Källa: nonuniform_circular_motion.PNG: BREWS OHRearivative Work: Kooning Jons [CC BY-SA 3.0 (https: // CreativeCommons.Org/licenser/BY-SA/3.0)].

Löst linjära hastighetsövningar

De lösta övningarna bidrar till att klargöra en korrekt användning av de angivna koncepten och ekvationerna.

-Motion Löst 1 

En insekt rör sig på en radie halvcirkel r = 2 m, börjar från vila vid punkten ett samtidigt öka dess linjära hastighet, med en hastighet av p m/s². Hitta: a) Efter vilken tid det når punkt B, b) den linjära hastighetsvektorn i det ögonblicket, c) vektoraccelerationen i det ögonblicket.

Figur 4. Ett insekt startar från A och når B på en halvcirkelformad bana. Den har en linjär hastighet. Källa: Självgjord.

Lösning

a) Uttalandet indikerar att tangentiell acceleration är konstant och är värd π m/s², Då är det giltigt att använda ekvationen för enhetligt varierad rörelse:

S (t) = s_antingen + v_antingenT + ½ a_T.t²

Med S_antingen = 0 och v_antingen = 0:

S (t) = ½ a_T.t²

S = πR (Hälften av omkretslängden)

T = (2. πR /till_T) ^½ S = (2π.2 /π)^½S = 2 s

b) v (t) = v_antingen + till_T. T = 2π Fröken

När vid punkt B pekar den linjära hastighetsvektorn i vertikal riktning ner i riktningen (-och):

Kan tjäna dig: vad är den dielektriska konstanten?

v (t) = 2π Fröken(-och)

c) Tangential acceleration har redan haft, centripetal acceleration saknas för att ha hastighetsvektorn till:

till_c = v² / R = (2π)² / 2 m/ s² = 2π² Fröken²

till = a_c (-x) + a_T (-och) = 2π²(-x)+ π (-och) Fröken²

-Motion Löst 2

En partikel vänder sig i en radiocirkel 2.90 m. I ett visst ögonblick är accelerationen värd 1.05 m/s² i en riktning så som bildas 32 med sin rörelsesriktning. Hitta din linjära hastighet på: a) Detta ögonblick, b) 2 sekunder senare, förutsatt att tangentiell acceleration är konstant.

Lösning

a) Rörelsedirektoratet är just den tangentiella adressen:

till_T = 1.05 m/s² . cos 32º = 0.89 m/s² ; till_C = 1.05 m/s² . Sen 32º = 0.56 m/s²

Hastigheten rensar till_c = v² / R som:

v = (r.till_c)^1/2  = 1.27 m/s

b) Ekvationen för enhetligt varierad rörelse är giltig enligt följande: v = v_antingen + till_TT = 1.27 + 0.89 .2² m/s = 4.83 m/s

Referenser

1. Bauer, w. 2011. Fysik för teknik och vetenskap. Volym 1. MC Graw Hill. 84-88.
2. Figueroa, D. Fysisk serie för vetenskap och teknik. Volym 3. Utgåva. Kinematik. 199-232.
3. Giancoli, D.  2006. Fysik: Principer med applikationer. 6^th... Ed Prentice Hall. 62-64.
4. Relativ rörelse. Återhämtat sig från: kurser.Lumenarning.com
5. Wilson, J. 2011. Fysik 10. Pearson Education. 166-168.