Vad är Coplanares Vectors? (Med lösta övningar)

De Coplanares vektorer o Coplanarios är de som finns på samma plan. När du bara har två vektorer är dessa alltid koppling.

Om du har tre eller flera vektorer kan det vara så att någon av dem inte är i samma plan som andra, därför kunde de inte betraktas som Coplanares. Följande figur visar en uppsättning coplanares betecknade i djärva vektorer TILL, B, C och D:

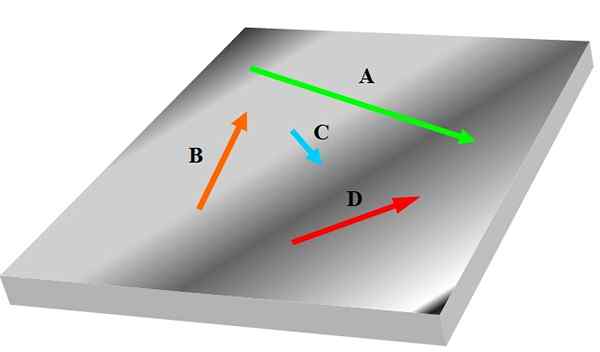Figur 1. Fyra coplanares. Källa: Självgjord.

Vektorer är relaterade till beteende och egenskaper hos relevanta fysiska storlekar inom vetenskap och teknik; till exempel hastighet, acceleration och styrka.

En kraft ger olika effekter på ett objekt när det sätt på vilket det tillämpas är varierat, till exempel att ändra intensitet, riktning och mening. Ändrar fortfarande en av dessa parametrar resultaten är betydligt olika.

I många applikationer, både i statisk och dynamik, är de krafter som verkar på en kropp på samma plan, därför betraktas de som Coplanares.

[TOC]

Förhållandena för att vektorer ska vara coplanares

För att tre vektorer ska vara coplanares måste de vara på samma plan och detta händer om de uppfyller något av följande förhållanden:

-Vektorer är parallella, därför är deras komponenter proportionella och är linjärt beroende.

-Din blandade produkt är ogiltig.

-Om du har tre vektorer och någon av dem kan skrivas som en linjär kombination av de andra två, är dessa vektorer coplanares. Till exempel en vektor som är resultatet av summan av två andra, de tre är alla i samma plan.

Kan tjäna dig: voltmeter: egenskaper, drift, vad är det för, typer

Alternativt kan villkoret för coplanaritet fastställas enligt följande:

U v w De är coplanarer om det finns tre siffror (skalor) α, β, y så att αeller + pv + yW = 0 Med (α, β, y) skiljer sig från (0, 0, 0)

Blandad produkt mellan tre vektorer

Den blandade produkten mellan vektorer definieras med tre vektorer eller, v och W, vilket resulterar i en skalar som är resultatet av att utföra följande operation:

eller · (v x W) = eller · (v x W)

Först görs korsprodukten som är inom parentes: v x W, vars resultat är en normal (vinkelrätt) vektor till planet där de är så v som W.

Ja eller är på samma plan som v och W, Naturligtvis måste den skalära produkten (punktprodukten) mellan u och den normala vektorn vara 0. På detta sätt verifieras det att de tre vektorerna är coplanares (de ligger på samma plan).

När den blandade produkten inte är noll, är resultatet lika med volymen på parallellepiped som har vektorerna eller, v och W som angränsande sidor.

Ansökningar

Coplanares, samtidiga och icke -kolineala krafter

Styrkorna samverkande De tillämpas alla på samma punkt. Om de också är Coplanares kan de ersättas av endast en, vilket kallas resulterande kraft Och det har samma effekt som de ursprungliga krafterna.

Om en kropp är i jämvikt tack vare tre coplanares, samtidiga och icke -kolineala (icke -parallella) krafter, kallade TILL, B och C, han Lamys teorem Han påpekar att förhållandet mellan dessa krafter (storlekar) är följande:

A / sin α = b / Sen β = c / Sen y

Med α, ß och y som vinklarna som motsätter sig de tillämpade krafterna, som visas i följande figur:

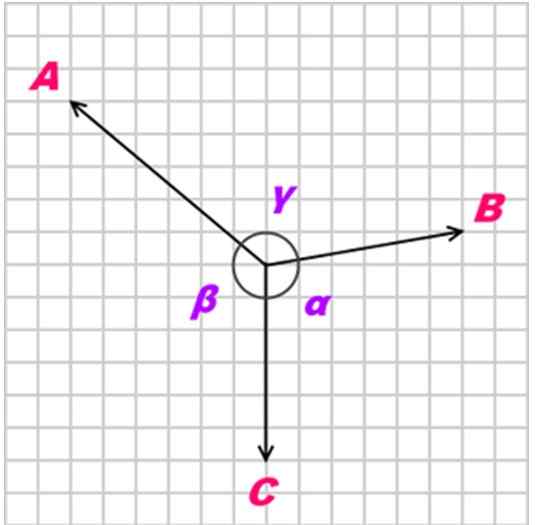figur 2. Tre krafter A, B och C Coplanares agerar på ett objekt. Källa: Kiwakwok på engelska Wikipedia [Public Domain]

Löst övningar

-Övning 1

Hitta värdet på k så att följande vektorer är coplanares:

Kan tjäna dig: Carnot Machine

eller =

v =

W =

Lösning

Eftersom komponenterna i vektorerna har haft används därför kriterierna för den blandade produkten: därför:

eller · (v x W) = 0

Det är löst först v x W. Vektorerna kommer att uttryckas i termer av enhetsvektorerna Yo, J och k som skiljer de tre vinkelräta riktningarna i rymden (bred, hög och djup):

v= 4 Yo + J + 0 k

W= -1 Yo + 2J -1 k

v x W = -4 (i x i) + 8 (i x j) - 4 (i x k) - (J x i) + 2 (J x j) - 2 (J x k) = 8 k + 4 J + k -2 i = -2 Yo + 4 J + 9 k

Den skalära produkten föreslås nu mellan U och vektorn som har resultat från föregående operation, matchande operation till 0:

eller · (v x W) = (-3 Yo + k J + 2 k) · (-2 Yo + 4 J + 9 k) = 6 + 4K +18 = 0

24 + 4k = 0

Det sökande värdet är: k = - 6

Så att vektorn eller är:

eller =

-Träning 2

Figuren visar ett objekt vars vikt är W = 600 N, hängande i balans tack vare kablarna placerade enligt vinklarna som visas i figur 3. Är det möjligt att tillämpa Lamys sats i denna situation? I alla fall hitta storleken på T₁, T₂ och T₃ som gör balans möjlig.

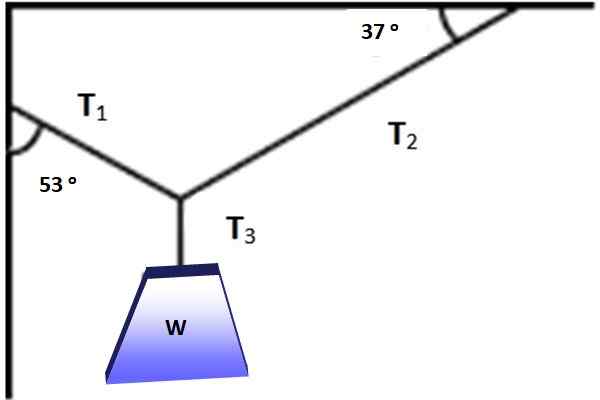Figur 3. En vikt hänger i jämvikt under verkan av de tre spänningar som visas. Källa: Självgjord.

Lösning

Lamys sats är tillämpligt i denna situation om knuten som de tre spänningarna tillämpas beaktas, eftersom de utgör ett system med coplanar krafter. Först är det fria kroppsdiagrammet gjord för hängvikten för att bestämma storleken på t_3:

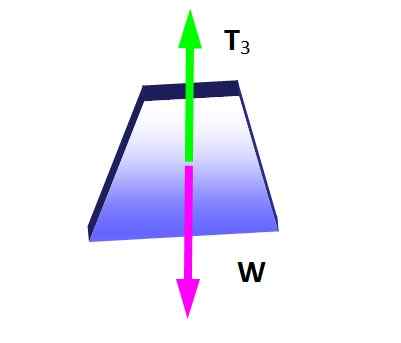Figur 4. Gratis kroppsdiagram för vikten hängande. Källa: Självgjord.

Från jämviktstillståndet följer det att:

Kan tjäna dig: diffraktion av ljud: vad är, exempel, applikationer

T₃  = W = 600 n

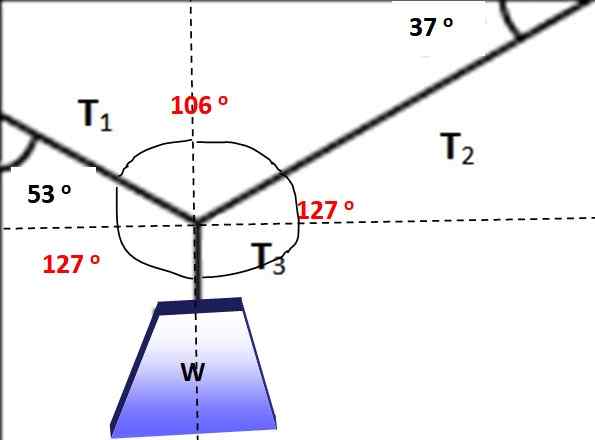
Vinklarna mellan krafterna är markerade i rött i följande figur, det kan lätt verifieras att dess summa är 360 °. Det är nu möjligt att tillämpa Lamys sats, eftersom en av krafterna och de tre vinklarna mellan dem är kända:

Figur 5.- I röda vinklarna för att tillämpa Lamys sats. Källa: Självgjord.

T₁ / Sen 127º = w / Sen 106º

Därför: T₁ = SEN 127º (W /SEN 106º) = 498.5 n

Återigen tillämpas Lamys sats för att rensa T₂:

T₂ / sin 127 = T₁ / Sen 127º

T₂ = T₁ = 498.5 n

Referenser

1. Figueroa, D. Serie: Physics for Science and Engineering. Volym 1. Kinematik. 31-68.
2. Fysisk. Modul 8: Vektorer. Återhämtat sig från: frtl.Utn.Edu.ar
3. Hibbeler, R. 2006. Mekanik för ingenjörer. Statisk. Sjätte upplagan. Continental Editor Company.28-66.
4. McLean, w. Schaumserie. Mekanik för ingenjörer: statisk och dynamisk. 3: e upplagan. McGraw Hill. 1-15.
5. Wikipedia. Vektor. Återhämtat sig från: det är.Wikipedia.org.