Korrespondensregel för en funktion

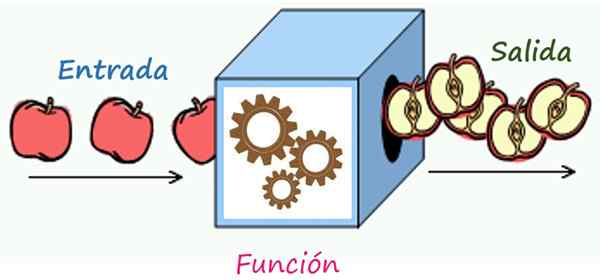
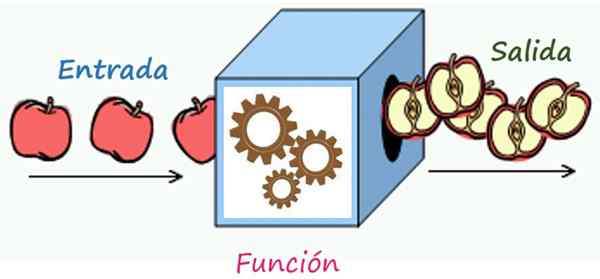Korrespondensregeln är en mekanism som förvandlar elementen i inträde i utgångselementen. Källa: Wikimedia Commons/F. Zapata

Vad är korrespondensregeln för en funktion?

De korrespondensregel för en funktion Påpeka hur elementen i en uppsättning är relaterade till elementen i en annan. Elementen i den första uppsättningen är kända som domän, och till de andra, som Kodominium antingen motom.

Förhållandet eller länken mellan uppsättningar kan specificeras genom verbal eller skriftlig instruktion, men när uppsättningarna är numeriska indikeras korrespondensregeln av en formel.

Denna formel innehåller de operationer som måste göras med elementen i startmonteringen och därmed få en serie element som ingår i kodominiet.

Nu, när förhållandet mellan elementen är en funktion, uppfyller korrespondensregeln två speciella förhållanden:

• Till vart och ett av elementen i domänen associeras, genom korrespondensregeln, ett enda element i kodominiet, känt som bild.
• Denna bild är unik, med andra ord, inget element i domänen är associerad med mer än ett element av kodominium.

På detta sätt kan du föreställa dig korrespondensregeln för en funktion som en mekanism låst i en låda. Varje domänvärde kan utan undantag komma in i rutan och komma ut ur den omvandlas genom de operationer som anges i korrespondensregeln. Exemplen kommer att ses omedelbart.

Exempel

Exempel 1

Korrespondensregeln för en funktion kan uttryckas som en skriftlig instruktion när elementen inte är numeriska.

Till exempel finns det en uppsättning länder, betecknade som P, och en annan uppsättning städer C:

Det kan tjäna dig: U -test av Mann - Whitney: Vad är det och när det appliceras, exekvering, exempel

P = Kanada, Mexiko, Spanien, USA, Frankrike, Argentina, Brasilien, Tyskland

C = Paris, London, Buenos Aires, Berlin, Mexico City, Ottawa, Río, New York, Madrid, Washington, Bern, Rom, Brasilia, Toronto

Vara korrespondensregeln F Mellan P och C som ges av:

F: P → C

Var F Det är regeln "... vars kapital är .. ”, Som associerar varje land i P (startuppsättningen), med sin huvudstad i C (ankomstuppsättningen).

Till exempel: ”Spanien, vars kapital är Madrid ". "Spanien" -elementet tillhör start -p -uppsättningen och "Madrid" -elementet till hela C, ankomsten.

Representationen av denna funktion kan göras genom ett Venn -diagram eller helt enkelt genom ordnade par.

Beställda par innehåller, som namnet antyder, två element med en specifik ordning, i detta exempel är det första elementet i paret landet, och det andra, dess huvudstad.

För sin del är Venn -diagrammet ett sätt att visualisera funktionen och visa start- och ankomstuppsättningarna, liksom korrespondensregeln mellan dem.

Representation av f som beställda par

F = (Kanada, Ottawa); (Mexiko, Mexico City); (Spanien Madrid); (USA; Washington); (Paris, Frankrike); (Argentina Buenos Aires); (Brasilien Brasilia); (Tyskland, Berlin)

Det första paret associerar Kanada, vars kapital är Ottawa, den andra associerar Mexiko, vars kapital är Mexico City och så vidare.

Representation av F som ett Venn -diagram

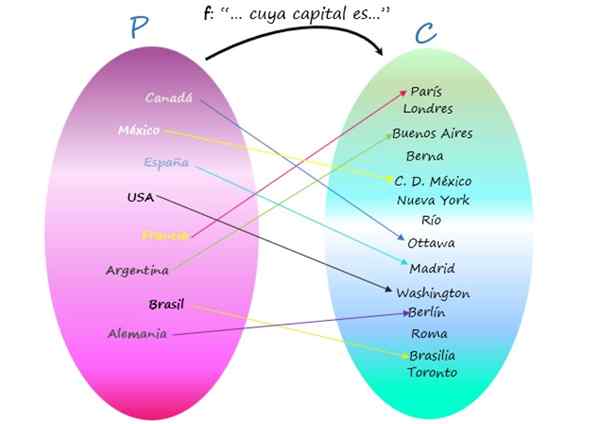
Observera att det finns städer som inte är huvudstaden i något land, eftersom även om de är delar av kodominiet är de inte en bild av någon del av startuppsättningen. Trots detta är förhållandet en funktion, eftersom det viktiga är att varje land har sitt kapital, och detta är unikt.

Kan tjäna dig: område med en vanlig och oregelbunden Pentagon: hur det tas, övningar

Undermängden som bildas av elementen i kodominiet som är bild av något element i domänen kallas Funktionens intervall eller funktion. För exemplet rutten R för F är:

R = Paris, Buenos Aires, Mexico City, Ottawa, Madrid, Berlin, Washington, Brasilia

Det är värt att fråga om en relation mellan C och P kan upprättas, där C blir startuppsättningen och ankomsten. Svaret är ja, men det skulle inte vara en funktion, eftersom det finns städer som inte är huvudstäder, till exempel New York, eller det land som de är kapital verkar inte bland elementen i P -komplexet, till exempel Rom.

Exempel 2

När avgångsuppsättningen och ankomstuppsättningen är numerisk är regeln om korrespondensen för funktionen som länkar dem en formel. Var till exempel behärskning av en funktion följande uppsättning:

D = 0, 1, 2, 3, 4, 5, 6)

Korrespondensregeln F: D → r som länkar elementen i d med uppsättningen av verkliga siffror r är:

F: "Dubbel"

Om "X" är ett element i startuppsättningen, är f (x) motsvarande element i ankomstuppsättningen, och korrespondensregeln är skriven så här:

f (x) = 2x

Codominium är uppsättningen av verkliga siffror. En delmängd av reais är rutten för denna funktion, uppsättningen siffror vars värde är dubbelt såsom x:

R = 0, 2, 4, 6, 8, 10, 12

I form av ordnade par resulterar korrespondensregeln i:

F = (0,0); (1.2); (2,4); (3,6); (4.8); (5.10); (6,12)

Beställda par kan vara graf vid det kartesiska planet. Det första elementet i vridmomentet placeras på den horisontella axeln, även kallad axeln för abscissas eller "x" -axeln, medan den andra går på den vertikala axeln, axeln för den ordnade eller helt enkelt axeln "y":

Kan tjäna dig: distribuerande egendom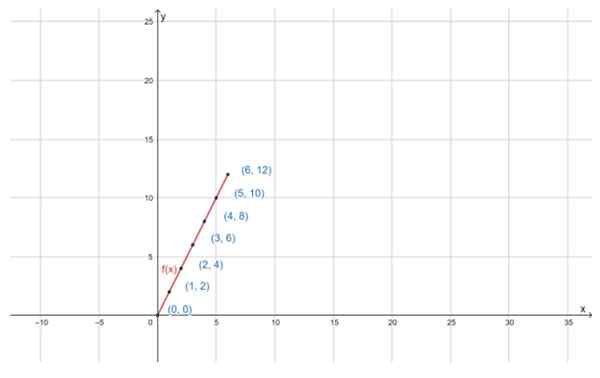 Grafen för funktionen f (x) = 2x, för den angivna D -domänen, är en rak linje. Källa: f. Zapata genom geogebra

Övningar

Bestäm korrespondensregeln för följande förhållanden, vilket indikerar om de är funktioner eller inte. Uppsättningen av naturliga siffror är n och det för det verkliga är r.

Ange också domänen, kodominiet och rutten för funktionen, i de fall där det motsvarar:

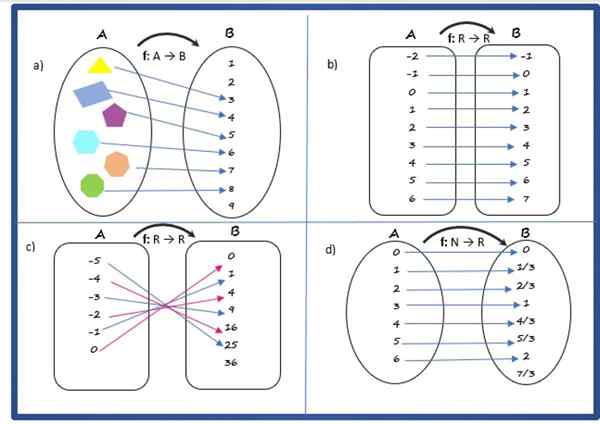
Lösning till

Det är en funktion, eftersom varje element i startuppsättningen, bestående av polygoner, har en unik bild i ankomstuppsättningen.

Korrespondensregeln relaterar polygonen till antalet sidor, domänen består av uppsättning A av polygonerna:

A = triangel, fyrkant, Pentagon, hexagon, hepton, åttkant

Codominium är uppsättningen av de första naturliga siffrorna, inklusive 0.

B = 0, 1, 2, 3, 4, 5, 6, 7, 8, 9

Och co c är de naturliga siffrorna från 3 till 8:

C = 3, 4, 5, 6, 7, 8

Lösning B

Det är en funktion, eftersom den uppfyller villkoren som anges ovan.

Korrespondensregeln är:

f (x) = x + 1

Korrespondensregeln indikerar att funktionen definieras av R → R, därför är domänen uppsättningen verkliga siffror. Och co -oominium och rutten sammanfaller också med det verkliga.

Lösning C

Det är en funktion med korrespondensregeln:

f (x) = x²

Domän och kodominium är uppsättning av reais, men rutten består endast av positiva verkliga siffror, betecknade som R⁺ och inklusive 0.

Lösning D

Det är en funktion. Dess korrespondensregel är:

f (x) = x/3

Dess domän är uppsättningen av naturliga nummer n och kodominium, såväl som rutten, är de verkliga n siffrorna r.