Högerhandregel
- 4279
- 492
- Per Eriksson
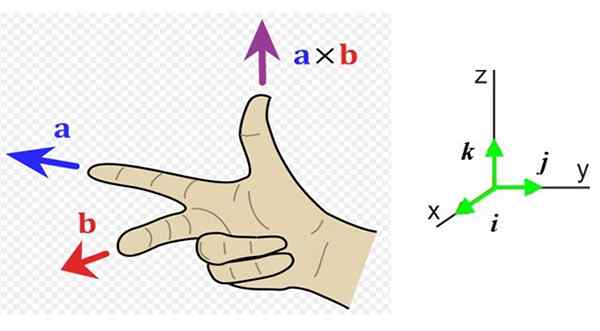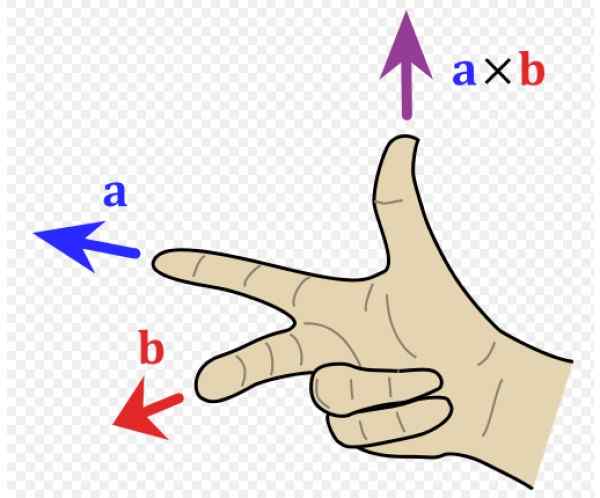
Figur 1. Högerhandregel. Källa: Wikimedia Commons. ACDX [CC BY-S (http: // Creativecommons.Org/licenser/BY-SA/3.0/]]. Vad är den högra regeln?
De högerhandregel Det är en mnemonisk resurs att fastställa riktningen och riktningen för vektorn till följd av en vektorprodukt eller tvärprodukt. Det används ofta i fysik, eftersom det finns viktiga vektorstorlekar som är resultatet av en vektorprodukt. Sådant är fallet med vridmoment, magnetisk kraft, vinkelmoment och magnetiskt ögonblick, till exempel.
Vara två generiska vektorer till och b vars tvärprodukt är till x b. Modulen för en sådan vektor är:
till x b = till.b.synd
Där α är minsta vinkel mellan till och b, Medan A och B representerar sina moduler. För att skilja vektorer från sina moduler används djärva bokstäver.
Nu måste vi veta riktningen och betydelsen av denna vektor, så det är bekvämt att ha ett referenssystem med de tre riktningarna för utrymmet (figur 1 till höger). Enhetsvektorerna Yo, J och k De pekar respektive på läsaren (ut ur sidan), till höger och uppåt.
I exemplet i figur 1 kvar, vektorn till är på väg till vänster (adress och negativ och pekfinger på höger hand) och vektorn b Går till läsaren (adress x Positiv, långfingret på höger hand).
Den resulterande vektorn till x b har tumriktningen, upp i riktning z positiv.
Den andra regeln för höger hand
Denna regel används mycket när det finns magnitud vars riktning och betydelse roterar, till exempel magnetfältet B produceras av en tunn och rätlinjig tråd som transporterar en ström.
I det här fallet är magnetfältlinjerna koncentriska omkretsar med tråden, och riktningen för svängen erhålls med denna regel enligt följande: den högra tummen indikerar riktningen för strömmen och de återstående fyra fingrarna är böjda i riktning mot riktningen fältriktning. Vi illustrerar konceptet i figur 2.
Kan tjäna dig: Elastiska chocker: I en dimension, specialfall, övningar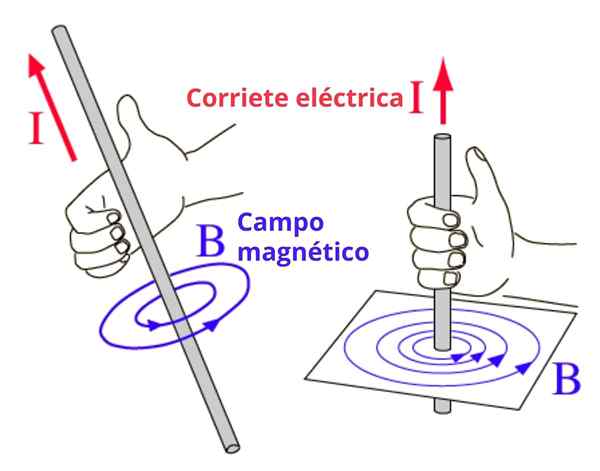
figur 2. Höger handregel för att bestämma betydelsen av magnetfältcirkulationen Högerhandens alternativ regel
Följande figur visar en alternativ form av högerhandregeln. Vektorerna som förekommer i upplysningen är:
- Fart v av en punktlig belastning som.
- Magnetfältet B inom vilken lasten rör sig.
- FB Den kraft som magnetfältet utövar på lasten.
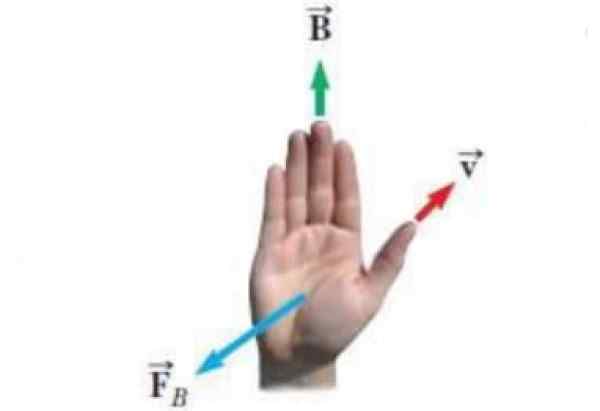Figur 3. Högerhandens alternativ regel. Källa: Wikimedia Commons. Experticuis [CC BY-SA (https: // CreativeCommons.Org/licenser/BY-SA/4.0)] Ekvationen för magnetisk kraft är FB = Qv x B och högerhandens regel för att veta riktningen och känslan av FB Det gäller så här: tummen pekar enligt V, de återstående fyra fingrarna placeras enligt fält B. Så FB Det är en vektor som kommer ut ur handflatan, vinkelrätt mot den, som om den pressade lasten.
Anteckna det FB skulle peka i motsatt riktning om belastningen som var negativ, eftersom vektorprodukten inte är kommutativ. Faktiskt:
till x B = - B x till
Ansökningar
Den högra regeln kan tillämpas på olika fysiska storlekar, låt oss veta några av dem:
Vinkelhastighet och acceleration
Båda vinkelhastigheten Ω Som vinkelacceleration a De är vektorer. Om ett objekt roterar runt en fast axel är det möjligt vinkelhastighet Ω.
För sin del är vinkelaccelerationen a kommer att ha samma adress som Ω, Men dess betydelse beror på om Ω ökar eller minskar sin storlek över tid. I det första fallet har båda samma riktning och betydelse, men i den andra kommer de att ha motsatta sinnen.
Kan tjäna dig: watt lag: vad är, exempel, applikationer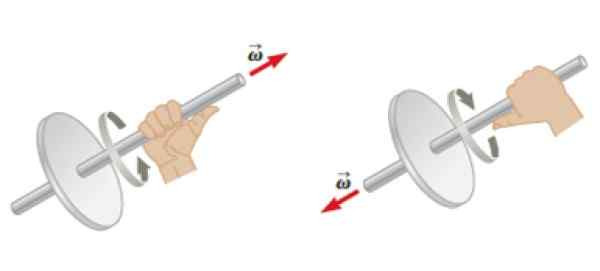
Figur 4. Högerregeln tillämpas på ett objekt i rotation för att bestämma riktningen och riktningen för vinkelhastigheten. Källa: Serway, R. Fysisk. Vinkelmomentet
Vinkelvektorn LANTINGEN av en partikel som roterar runt en viss axel eller definieras som vektorprodukten från dess omedelbara positionsvektor r och mängden linjär rörelse p:
L = r x p
Den högra regeln tillämpas på detta sätt: pekfingret placeras i samma riktning och riktning för r, Långfingret i p, båda på ett horisontellt plan, som i figuren. Automatiskt sträcker tummen vertikalt uppåt och pekar ut riktningen och riktningen för vinkelmomentet LANTINGEN.
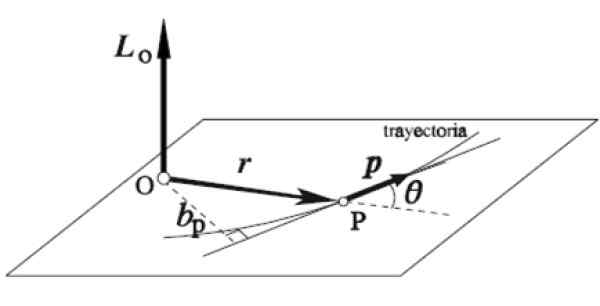Figur 5. Vinkelvektorn. Källa: Wikimedia Commons. Övningar
Övning 1
Spinet i figur 6 går snabbt med vinkelhastighet Ω och dess symmetriaxel bröts långsamt runt den vertikala axeln z. Denna rörelse kallas precession. Beskriv de krafter som verkar på snurret och effekten de producerar.
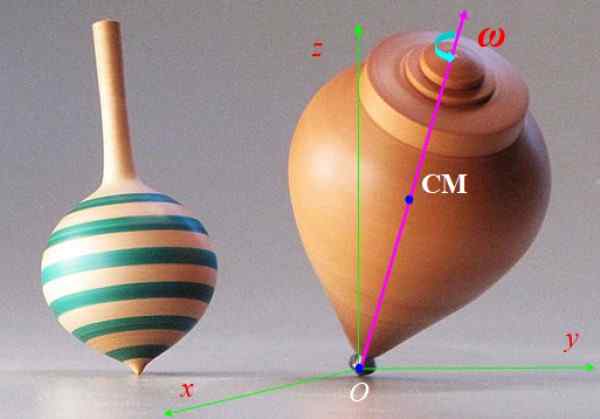Figur 6. Snurrspinn. Källa: Wikimedia Commons. Lösning
Krafterna som verkar på snurret är normala N, tillämpas på stödpunkten med marken eller mer vikten mg, tillämpas i mitten av massan CM, med g Svårighetsaccelerationsvektorn, riktad vertikalt ner (se figur 7).
Båda krafterna är balanserade, därför rör sig inte snurret. Vikten producerar dock ett vridmoment eller vridmoment τ Netto om punkten eller, ges av:
τANTINGEN = rANTINGEN x F, med F = Mg.
Som r och Mg De är alltid på planet när snurret vänder sig, enligt regeln för höger hand vridmomentet τANTINGEN Det är alltid beläget i planet Xy, vinkelrätt båda a r som g.
Anteckna det N producerar inte ett vridmoment med avseende på O, eftersom dess vektor r Angående eller är null. Det vridmomentet ger en förändring i vinkelmomentet som orsakar pressen på snurret runt z -axeln.
Kan tjäna dig: termodynamisk balans: klasser och applikationer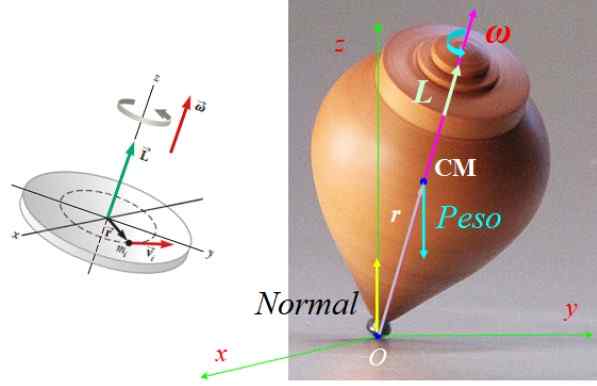
Figur 7. Krafter som verkar på snurret och dess vinkelmomentvektor. Källa till vänster figur: Serway, R. Fysik för vetenskap och teknik. Övning 2
Påpeka riktningen och riktningen för vinkelmomentvektorn L av trumman i figur 6.
Lösning
Varje punkt i snurret har massa mYo, fart vYo och positionsvektor rYo, När den kretsar kring z -axeln. Vinkelmomentet LYo av nämnda partikel är:
LYo = rYo x pYo = rYo x mYovYo
Med tanke på rYo och vYo De är vinkelräta, storleken på L är:
LYo = mYorYovYo
Den linjära hastigheten v är relaterad till vinkelhastigheten Ω genom:
vYo = rYoΩ
Därför:
LYo = mYorYo (rYoΩ) = mYorYo2Ω
Trompoens totala vinkelmoment är summan av vinkelmomentet för varje partikel:
L = (∑mYorYo2 ) Ω
∑ mYorYo2 Det är tröghetsmomentet i, då:
L= JagΩ
Därför L och Ω De har samma riktning och betydelse, som visas i figur 7.