Spakregel

Vad är spakregeln?

De spakregel Det är ett matematiskt förfarande som gör det möjligt att beräkna fraktioner, procentsatser eller mängder av de faser som finns i balans inom ett binärt system. Det är inte bara matematiskt, utan också ganska grafiskt och självhäftande, att vara mycket användbar i fysikalisk -kemiska och tekniska beräkningar.

Denna regel gäller för fasdiagram för binära system, oavsett typ av system i sig själv. Det vill säga, faserna kan vara solida, som med legeringarna; eller vätska och gasformigt, som vi ser i system i vätskevaporjämvikt.

Den fysiska och matematiska principen för spaken används också för kemiska ändamål och i materialets fysik. Källa: Jimbowley, CC BY-SA 3.0, via Wikimedia Commons

Spakregeln kan tillämpas direkt med hänsyn till värden grafik i Abscissas axel, där de globala fraktionerna eller procentandelarna av den mest flyktiga komponenten vanligtvis går, i fallet med vätskor; eller eldfast, i fallet med metaller i deras legeringar.

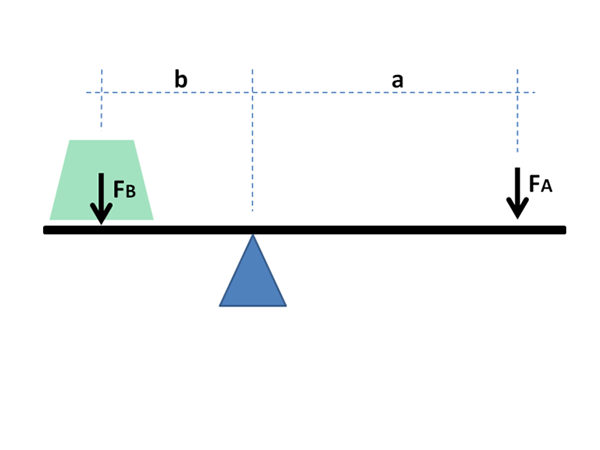
Som kommer att ses nedan beror dess namn på den enorma likhet det har med de matematiska uttryck som visar balansen mellan två massor som ligger i ändarna av en rocker med Fulcro.

Spakarmarna måste balansera för att balansera massorna på lasterna; När det gäller fasdiagram, fraktioner och mol i faserna i materialjämvikt.

Förklaring

Grafiska aspekter

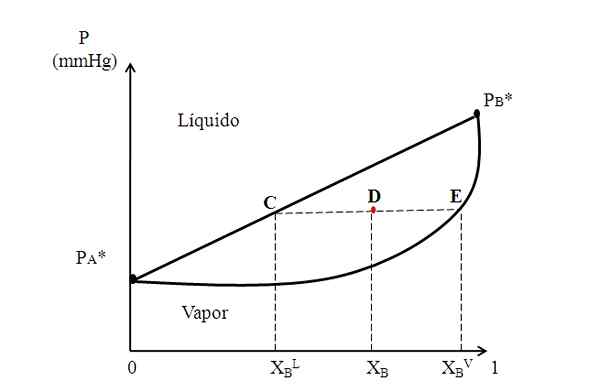Hypotetiskt binärt diagram där en bindande linje visar sammansättningar av vätskan och ångfaserna. Källa: Gabriel Bolívar.

Mitt i diagrammet ovan har vi en region där vätska och ånga samexisterar; Det vill säga vätskevaporns jämviktsregion. Ovanför denna region kommer blandningen av A och B att vara flytande, och under den kommer att vara soda på grund av det lägre tryck.

Tänk nu på en blandning med en X -komposition_B och vars tryck placerar det vid punkt D. Vi drar från punkten D en horisontell linje som rör vid linjen och kurvan på sidorna, med ursprungspunkter C respektive E. Denna linje, som kommunicerar punkter C, D och E, C-D-E, är den som kallas Unionslinjen och genom att projicera den mot axeln och måste ge oss systemets tryck.

Det kan tjäna dig: vatten alkalinitet: vad är, beslutsamhet och betydelse

Sedan drar vi från dessa punkter andra linjer vinkelrätt mot bindningslinjen, som kommer att spela X -axeln. Eftersom punkt E vilar på ångkurvan, kommer vi att ha den molära fraktionen av B i ångfasen (x_B^V). På samma sätt kommer punkt C, på den raka vätskan, att ge oss den molära fraktionen av B i vätskefasen (x_B^L).

Spakregeln är baserad exakt på bindningslinjen och avståndet mellan x_B^L, X_B och x_B^V.

Matematisk avdrag

Den globala molära fraktionen av B är lika med:

X_B = n_B / (n^L + n^V)

Var n_B De är de totala molen av B både i vätskan och ångfasen, och n^L och n^V är respektive mol för dessa faser. Clearing n_B vi kommer att ha:

n_B = X_Bn^L + X_Bn^V (1)

Å andra sidan, n_B Det är också lika med:

n_B = n_B^L + n_B^V

= X_B^Ln^L + X_B^Vn^V  (2)

Nu utjämnar ekvationerna (1) och (2) oss:

X_Bn^L + X_Bn^V = X_B^Ln^L + X_B^Vn^V

Och ordna om:

n^L(X_B - X_B^L) = n^V(X_B^V - X_B) (3)

n^L(C-d) = n^V(AV)

Dessa två sista matematiska uttryck är spakregeln. Observera att x_B - X_B^L Det är avståndet mellan punkterna C och D; och x_B^V - X_B, Det är avståndet mellan punkterna D-E: de två halvorna av bindningslinjen (spakarmar).

Denna ekvation är mycket lik den som beskriver balansen mellan massorna på en rocker med Fulcro:

m₁l₁ = m₂l₂

Således kommer spakregeln att tillåta oss att beräkna de totala mullvadarna n^L och n^V under förutsättning att blandningens totala mol är kända, n_T (n_T = n^L + n^V).

Andra form

Det tidigare uttrycket för spakregeln tjänar till att beräkna mängderna (massor, mol, etc.) av faserna i jämvikt. Men den mest kända versionen av spakregeln gör det möjligt för oss att beräkna fraktionerna eller procentandelarna i varje fas, med bara avståndet mellan x_B, X_B^L och x_B^V.

Tänk på samma system ovan, med en annan form av spakregeln:

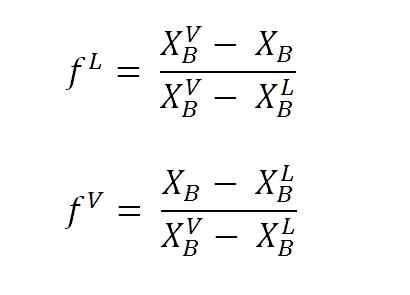Ekvationer för att beräkna vätska och ångfraktioner med spakarmarna. Källa: Gabriel Bolívar.

Var F ^L och F ^VDe är molära fraktioner (eller procent, beroende på grafen) för vätskan respektive ångfaser. Observera att det uppenbarligen, F ^L och F ^V De har inga enheter; medan n^L och n^V Ja, de har enheter (mol, gram, etc.).

Kan tjäna dig: reaktionsvärme

Exempel

Metod 1

I en behållare blandas 28 mol B och 12 mol A. Bestäm mängder och molära fraktioner för de faser som bildas.

Vi beräknar x_B:

X_B = (28 mol b)/ (28 mol B + 12 mol a)

= 0.7

Detta värde motsvarar x_B av toppdiagrammet. Avlyssningarna kommer att ge oss ungefär följande värden för x_B^L och x_B^V:

X_B^L = 0.41

X_B^V = 0.94

Med spakregeln:

n^L(X_B - X_B^L) = n^V(X_B^V - X_B)

Och att veta det n_T = n^L + n^V, och? n_T = 40 mol, då rensar vi n^L antingen n^V beroende på den andra:

n^L(X_B - X_B^L) = (40 mol - n^L) (X_B^V - X_B)

Omarrangera och rensa n^L vi kommer att ha:

n^L = (40 mol) (x_B^V - X_B) / (X_B^V - X_B^L)

Kommer inte detta uttryck ihåg det av F ^L? Nu ersätter vi:

n^L = (40 mol) (0.94 - 0.70) / (0.94 - 0.41)

= 18.11 mol i flytande fas

Vi kan beräkna n^V På två sätt:

n^V = n^L(X_B - X_B^L) / (X_B^V - X_B)

antingen

n^V = 40 mol - 18.11 mol

= 21.89 mol i ångfas

Metod 2

Vad händer om vi beräknar först F ^L och F ^V?

F ^L = (X_B^V - X_B) / (X_B^V - X_B^L)

= (0.94 - 0.70) / (0.94 - 0.41)

= 0.4528 eller 45.28%

Det vill säga 45.2% av mullvadarna befinner sig i en flytande fas, vilket är det beloppet lika med:

n^L = F ^Ln_T

= (0.4528) (40 mol)

= 18.11 mol

OCH F ^V Vi kan beräkna det lika på två sätt:

F ^V = 1 - F ^L

antingen

F ^V = (X_B - X_B^L) / (X_B^V - X_B^L)

Att vara dess värde:

F ^V = 0.5472 eller 54.72%

Och därför, n^V Det kommer att vara lika med:

n^V = F ^Vn_T

= (0.5472) (40 mol)

= 21.89 mol

Observera att tillämpning av de två formerna av spakregeln som alternativa beräkningsmetoder kan samma resultat uppnås. Metod 2 verkar mer direkt och enkel; men om det observeras noggrant när rensningen har lösts n^L antingen n^V, Det kommer att ses att båda metoderna faktiskt är lika enkla.

Löst övningar

Därefter kommer två andra övningar att lösas, där nu de system som övervägs kommer att involvera en vätskefast och icke-vätskevapor. Diagrammen är också grafiska med avseende på systemtemperaturen och inte deras tryck.

Övning 1

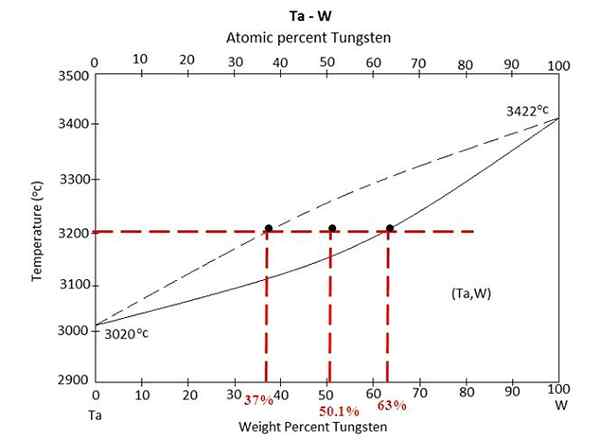Fasdiagram för en legering mellan Tantalo och volfram. Källa: Materialpedia, CC BY-SA 4.0, via Wikimedia Commons

Vi har fasdiagrammet ovanför en legering mellan Tantalo och volfram, ta-w. På x -axeln representeras de globala massprocenten av volfram, w% (m/m).

Inom den vätskedjämviktsregionen (TA+W) och fast (legering) finns en blandning vid 3200 ºC. Bestäm massorna i varje fas förutsatt att 100 gram av legeringen värms upp.

Det kan tjäna dig: metaller, icke -metaller och metalloider

Procedur

Den här gången kommer övningen att lösas med hjälp av den andra formen av spakregeln. Unionslinjen berättar för oss att: I den solida fasen har vi 63% av volfram, medan vi i vätskefasen har 37% volfram. Detta beror på att volframen smälter till en högre temperatur (3422 ºC) än tantalen (3020 ºC).

Så vi har:

W%^S eller w_S= 63%

W%^L eller w_L= 37%

Och även:

W₀ = 50.1%

Vi tillämpar spakregeln på F ^L:

F ^L = (63% - 50.1%) / (63% - 37%)

= 0.4961 eller 49.61%

Observera att avståndet som motsvarar vätskefasen är spakarmen nära den fasta fasen, den motsatta sidan av mediumpunkten.

Massan i vätskefasen är därför:

(0.4961) (100 gram) = 49.61 smält gram

Och den fasta fasen kommer att vara lika med:

100 gram - 49.61 gram = 50.39 gram av legering rik på volfram

Övning 2

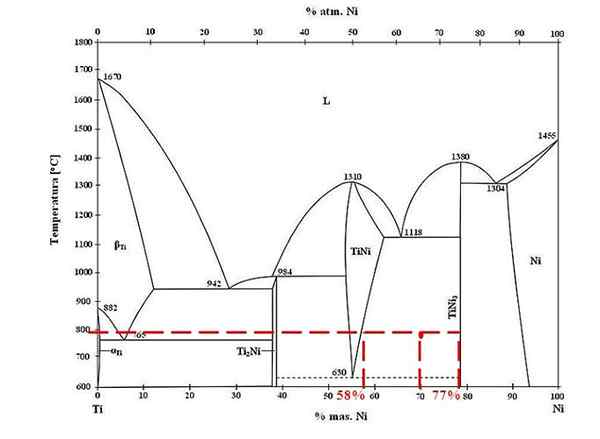Fasdiagram för titan-nickellegeringar. Källa: Doomgiver, CC BY-SA 3.0, via Wikimedia Commons

För titan- och nicklegeringen vid 800 ºC, och med 70% nickel, bestäm hur mycket av Tini och Tini₃ De är närvarande.

Procedur

Den här gången ber de bara om massfraktionerna i varje fas. Den röda punkten är belägen i jämviktsområdet mellan Tini- och Tini -faserna₃, vars kurvor är där den spelar unionslinjen som flyter till värdena på 58% eller för Tini -fasen och 77% eller för Tini -fasen₃.

Observera att den röda punkten är närmare Tini -fasen₃ det i Tini -fasen. Detta betyder att det måste finnas mer tini₃ den tini; Och därför avståndet eller spakarmen som motsvarar Tini₃ Det måste vara den längsta, det motsatta (70%-58%).

Genom att veta detta fortsätter vi att beräkna F ^Tini3:

F ^Tini3 = (70% - 58%) / (77% - 58%)

= 0.6316 eller 63.16%

Faktum är att 63.16% av legeringen motsvarar Tini -fasen₃. Samtidigt motsvarar Tini -fasen:

1 = F ^Tini3 + F ^Tini

F ^Tini = 1 - F ^Tini3

= 0.3684 eller 36.84%

Sammanfattningsvis till de uppförda övningarna kan vi säga att spakregeln är till stor hjälp för att bestämma fraktionerna för varje fas i jämvikt för ett tvåkomponentsystem.

Referenser

1. Walter J. Moore. (1963). Fysisk kemi. I kemisk kinetik. Fjärde upplagan, Longmans.
2. Iran. Levin. (2009). Principer för fysikalik. Sjätte upplagan. MC Graw Hill.
3. Wikipedia. (2020). Spakregel. Hämtad från: i.Wikipedia.org
4. Michael Adewumi. (18 maj 2020). Spakregeln. Återhämtad från: Eng.Librettexts.org
5. Adam Warren. (1997). Fasdiagram: Bindlinjer och spakregeln. Återhämtat sig från: Southampton.Växelström.Storbritannien
6. Universitetet i Cambridge. (2020). Spakregeln. Hämtad från: doitpoms.Växelström.Storbritannien