Fibonacci -serieegenskaper, naturliga relationer, applikationer

De O serie Fibonacci -succession är en sekvens av siffror som erhålls genom att börja med 0 och 1, fortsätter med summan av dem: 0 + 1 = 1, sedan summan av de två föregående: 1 + 1 = 2 och så vidare.

Efter denna procedur erhålls de andra termerna, låt oss se: 2 + 1 = 3, 3 + 2 = 5, 5 + 3 = 8, 8 +5 = 13 ..

Första numren i Fibonacci -serien

Proceduren upprepas så många gånger du vill. På detta sätt förvärvar Fibonaccis succession formuläret: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 .. Siffrorna som gör det kallas Fibonacci -nummer.

[TOC]

Historia

Fibonaccis arv kallas en italiensk matematiker som bodde under medeltiden: Leonardo de Pisa, även känd som Fibonacci (1175-1250). 

Leonardo de Pisa

Leonardo tillbringade barndomen i Nordafrika och reste i hela Medelhavet, där han kände till Indo -arabiska numreringssystemet och var nöjd med honom. Förmodligen lärde Leonardos arabiska lärare honom om arv, som redan var känd av hinduiska matematiker.

Därefter, när han återvände till Pisa Fibonacci skrev en bok som heter Liberbaci (Abacus bok), där han förutom att lyfta fram fördelarna med indo -arabiska nummer inför romersk numrering och introducera 0, tog han upp ett problem om reproduktionen av kaniner.

Och lösningen på detta problem är just antalet Fibonacci -succession.

Leonardo de Pisa tilldelades inte skapandet av arv; Han nämnde det bara i sin bok som en nyfikenhet, som fick uppmärksamhet från många forskare som följde honom. Bland dessa var den nittonde århundradet franska matematikern Edouard Lucas, som när han studerade successionen döpt henne med namnet på den medeltida vismannen som gjorde det känt i väst.

Problemet med Fibonacci -kaniner

Problemet säger: Det finns ett par kaniner som lever för evigt, vilket vid två månader är bördig. När mognaden har uppnåtts har de ett par barn med olika sex varje månad, som också tar två månader att reproducera och ha ett månatligt par kaniner.

Kan tjäna dig: de morgan lagar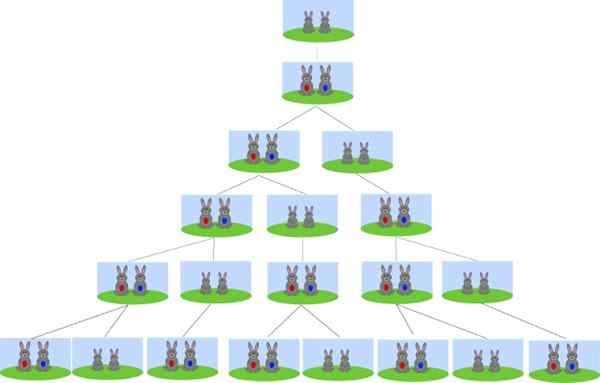Ursprunget till Fibonaccis arv är i problemet med reproduktion. Källa: Wikimedia Commons.

Börjar med ett par nyfödda kaniner, hur många par kaniner kommer att vara om en månad? Hur många par kaniner kommer att vara efter 2, 3 och 4 månader? Och hur många som kommer att vara efter 6 månader?

Svaret är i Fibonacci -nummer. Efter en månad finns ett par kaniner, det ursprungliga paret, eftersom de bara reproducerar efter 2 månader.

Efter 2 månader finns det två par kaniner: det ursprungliga paret och deras första kull.

Efter 3 månader kommer vi att ha 3 par, inklusive det ursprungliga paret, deras första kull och ett nytt.

När vi når den fjärde månaden kommer vi att ha det ursprungliga paret, det första kullen som i sin tur har sina första barn, den tredje månadens kull och en ny kull. Totalt 5 par kaniner.

Men det här är antalet Fibonacci -sekvens, därför kommer det efter 6 månader att finnas 13 par kaniner, eftersom paren under de föregående två månaderna läggs till varje månad.

Fibonacci -serieegenskaper

Här är några intressanta egenskaper hos Fibonacci -successionen.

Egendom 1

Den rekursiva formeln för att hitta villkoren för arv är:

till_N+1 = a_n + till_N-1  För n större än eller lika med 2.

Där n = 2, 3, 4, ... det vill säga att hitta den sjunde termen a₇, Vi gör n = 6, så att 6+1 = 7. Vi måste veta villkoren till₅  redan₆, av listan som visas i introduktionen till₅ = 5 och a₆ = 8, därför till₇ = 5+8 = 13.

Egendom 2

Om de två termerna vi vill hitta inte är kända, kan vi använda följande formel:

Det kan tjäna dig: Tesseldos: karakteristiska, typer (vanliga, oregelbundna), exempel

Egendom 3

Siffrorna a_n redan_N+1 are  Coprimos, Det vill säga de är kusiner med varandra, vilket innebär att de inte har några vanliga faktorer gemensamt.

Egendom 4

En mycket intressant egenskap är kvoten mellan villkoren till_2n redan_n, vilket är värt 1, när n = 1. Det vill säga:

till₂ till₁ = 1

Vi kan enkelt kontrollera det med listan över Fibonacci -nummer.

Å andra sidan, om n ≠ 1, är kvoten:

till_2n till_n = a_n  + 2: a_N-1

Till exempel om n = 3, då a _2n = a₆ = 8 och₃ = 2. Okej då:

8/2 = 2 + 2. till₂ = 2 + 2. 1

Faktiskt: 8/2 = 4 och 2 + (2.1) = 4. Det kan verifieras att alla n -värde uppfylls.

Egendom 5

Förhållandet r_n = a_N+1 till_{n ,} När N blir stor, konvergerar till Guldskäl antingen Aurea -andel, Ett irrationellt antal som uppstår ofta i naturen, ges av:

Naturliga relationer mellan Fibonacci -successionen

Fibonaccis arv i växter

Manifestationerna av Fibonacci -successionen finns i överflöd i växtriket

Grenarna av vissa träd kommer ut varje år enligt Fibonacci -successionen. Det första året stammen växer utan att kasta någon gren, efter ett år producerar den en och så under varje år. I sin tur kan varje gren kasta en ny efter ett år, precis som kaninerna reproducerar.

Solflower Flowers Center innehåller frön som arrangeras i logaritmiska spiralstrålar, i båda mening, vars mängder motsvarar två på varandra följande Fibonacci -nummer.

Fibonacci -nummer finns i antalet solros- och margaritblommor kronblad, liksom i många mönster där växter har sina blad.

Kan tjäna dig: ordinär variabel

Experter säger att växter på detta sätt optimerar utrymmet för blad och blommor för att få optimal tillväxt.

Med en central punkt som startplats växer och får dessa strukturer, därför måste de nya bladen och kronbladen täcka så lite som möjligt de som kom ut först. Och det bästa sättet att uppnå detta är att anta ett tillväxtmönster när det gäller Fibonacci -sekvensen.

Fibonaccis succession hos djur

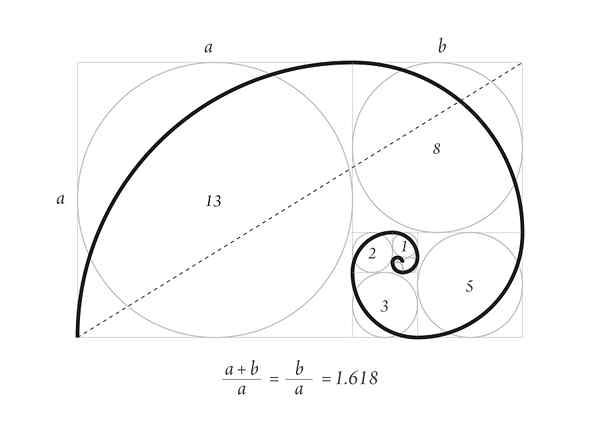Dureros spiral med det första antalet Fibonaccis succession

Den hållbara spiralen i den överlägsna bilden är en del av tillväxtmönstret för skalen i marina djur och hornen hos vissa idisslare.

Börja med två rutor 1, en ovanpå den andra, sedan en kvadrat av sidan 2 bredvid den, vilket utgör en rektangel av sidan 3, vars sidor har den gyllene proportionen.

Nedan är en kvadrat av sidan 3 och till vänster en kvadrat av sidan 5. Ovanför finns en kvadrat av sidan 8 och till höger en kvadrat av sidan 13. Det här är de första siffrorna.

Slutligen dras spiralen genom att röra vid punkterna på rutorna på rutorna, som ses i figuren.

Ansökningar

Fibonaccis succession tillämpas inom olika områden:

-I konst visas den gyllene andelen relaterad till arv efter Fibonacci hos människor och saker som representeras av stora konstnärer som Leonardo da Vinci, Miguel Ángel och Alberto Durero.

-Partnerens proportioner i Aten svarar också på guldantalet.

-I kompositionerna av Mozart, Beethoven, Schubert och Debussy.

-Att designa föremål vars proportioner ser harmoniska ut för mänskliga ögon, till exempel kreditkort, containrar, flaggor.

-På aktiemarknaden används det för att förutsäga vilka priser som återgår sin trend.

Referenser

1. Fibonacci succession. Återhämtat sig från: bloggeducastur.är.
2. Stewart, J. 2007. Förkalkning. Femte. Utgåva. Cengage Learning.
3. Vargas, m. Fibonacci successionsapplikationer. Återhämtat sig från: Matesup.Kli.
4. Wikipedia. Fibonacci. Hämtad från: i.Wikipedia.org.