Linjära vågor koncept, egenskaper, exempel

De Linjära vågor Dessa är de där superpositionsprincipen är tillämplig, det vill säga de där vågformen och dess rymdtidsutveckling kan uppnås som summan av grundläggande lösningar, till exempel på harmonisk typ. Inte alla vågor möter superpositionsprincipen, som inte följer den kallas icke-lineala vågor.

Den "linjära" valören kommer från det faktum att linjära vågor alltid uppfyller en differentiell ekvation i partiella derivat, där alla termer som involverar den beroende variabeln eller dess derivat höjs till den första kraften.

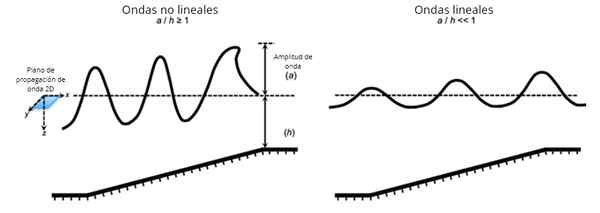
Vågorna som ses på avstånd är linjära vågor, men de rädda vågorna i förgrunden är icke-lineala. Källa: Pixabay.

Å andra sidan tillfredsställer icke-lineala vågor vågekvationer som har kvadratiska eller högre grader i den beroende variabeln eller i deras derivat.

Ibland är det förvirrat att linjära vågor med longitudinella vågor, som är de där vibrationer inträffar i samma förökningsriktning, såsom ljudvågor.

Men longitudinella vågor, såväl som transversala, kan i sin tur vara linjära eller icke-linjära beroende på bland andra faktorer amplituden av den initiala störningen och miljön där de sprider sig.

Det inträffar i allmänhet att när den initiala störningen är av liten amplitud, är ekvationen som beskriver utbredningen av vågen, av linjär typ eller kan linjas av vissa tillvägagångssätt, även om den inte alltid är så.

[TOC]

Differentiell ekvation i linjära vågor

I ett linjärt medium kan en begränsad vågform i rymden och tiden representeras av summan av sinus eller kosinusvågfunktioner för olika frekvenser och våglängder via Fourier -serien. 

Linjära vågor har alltid en differentiell ekvation av den linjära typen som är associerad, vars lösning representerar förutsägelsen av vad som kommer att vara störningen i bakre stunder av en initial störning som ligger rumsligt vid det första initiala ögonblicket.

Den klassiska linjära vågekvationen, i en enda rumslig dimension, vars lösningar är linjära vågor är:

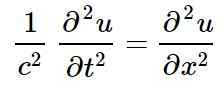
I föregående ekvation eller representerar störningen av en viss fysisk mängd i positionen x Och just nu t, det vill säga eller Det är en funktion av x och t:

Det kan tjäna dig: vad är coplanares vektorer? (Med lösta övningar)

u = u (x, t)

Till exempel, om det är en ljudvåg i luften, eller Det kan representera variationen i trycket med avseende på dess värde utan att störa.

När det gäller en elektromagnetisk våg, eller representerar det elektriska fältet eller magnetfältet som svänger vinkelrätt mot förökningsriktningen.

I fallet med ett spänt rep, eller Representerar tvärförskjutningen med avseende på balansen i repets jämvikt, som visas i följande figur:

Vågform i ett givet ögonblick, i fallet med linjära vågor är denna form överlappningen av sinusformade vågor med olika frekvens och våglängder. Källa: f. Zapata.

Differentiella ekvationslösningar

Om du har två eller flera lösningar av den linjära differentiella ekvationen, kommer varje lösning multiplicerad med en konstant att vara en lösning och kommer också att vara summan av dem. 

Till skillnad från icke-linjära ekvationer, medger Waveline-ekvationer harmoniska lösningar av typen: 

eller₁= A⋅sen (k⋅x - ω⋅t) och eller₂= A⋅sen (k⋅x + ω⋅t) 

Detta kan verifieras genom enkel substitution i den linjära vågekvationen.

Den första lösningen representerar en progressiv våg som går framåt till höger, medan den andra till vänster snabbt C = ω/k.

Harmoniska lösningar är karakteristiska för linjära vågekvationer.

Å andra sidan är den linjära kombinationen av två harmoniska lösningar också en lösning på den linjära vågekvationen, till exempel:

u = a₁ cos (k₁⋅x - ω₁⋅T) + a₂ handfat₂⋅x - ω₂⋅t) är lösning.

Det mest relevanta kännetecknet för linjära vågor är att någon form av våg, oavsett komplexa, kan erhållas med en summa enkla harmoniska vågor i bröst och kosinus:

u (x, t) = a₀ + ∑_n TILL_n cos (k_n⋅x - ω_n⋅t) + ∑_m B_m handfat_m⋅x - ω_m⋅t).

Spridande och icke -dispersiva linjära vågor

I den klassiska linjära vågekvationen, c representerar hastigheten för utbredning av pulsen.

Icke -olika vågor

I fall där c Det är ett konstant värde, till exempel de elektromagnetiska vågorna i tomrummet, sedan en puls vid det första ögonblicket t = 0 Form f (x) Det sprider sig enligt:

u (x, t) = f (x - c⋅t)

Utan att drabbas av någon snedvridning. När detta inträffar sägs det att mediet är icke-design.

Spridande vågor

I spridande media kan emellertid förökning C -hastigheten bero på våglängden λ, det vill säga: C = C (λ).

Kan tjäna dig: kontinuitetsekvation

Elektromagnetiska vågor är spridda när du reser genom ett materialmedium. Även ytvågorna på vatten reser med olika hastighet beroende på vattendjupet.

Hastigheten med vilken en harmonisk våg sprider sig A⋅sen (K⋅X - ω⋅t) är Ω/k = c och fashastigheten kallas. Om mediet är spridande, då c Det är en vågnummerfunktion k: C = c (k), var k Det är relaterat till våglängden med hjälp av K = 2π/λ.

Spridningsförhållanden

Förhållandet mellan frekvens och våglängd kallas spridningsförhållande, som uttrycktes i termer av vinkelfrekvens Ω och vågnumret k är: Ω = c (k) ⋅k.

Vissa spridningsförhållanden Egenskaper för linjära vågor är följande:

I vågorna där våglängden (avståndet mellan åsar) är mycket större än djupet H, Men att dess bredd är mycket mindre än djupet är spridningsförhållandet:

Ω = √ (gh) ⋅k

Därifrån dras det att de sprids med konstant hastighet √ (gh) (icke -dispersiv hälft).

Men vågorna i mycket djupa vatten är spridda, eftersom deras spridningsförhållande är:

ω = √ (g/k) ⋅k

Detta betyder att fashastigheten Ω/k Det är varierande och beror på vågnumret och därför våglängden för vågen.

Grupphastighet

Om två harmoniska linjära vågor överlappar varandra men går vidare med olika hastigheter, matchar inte grupphastigheten (det vill säga av vågpaketet) inte fashastigheten.

Grupphastighet v_g Det definieras som frekvensderivatet med avseende på vågnumret i spridningsförhållandet: v_g = Ω '(k).

Följande figur visar överlappningen eller summan av två harmoniska vågor eller₁= A⋅sen (k₁⋅x - ω₁⋅t) och eller₂= A⋅sen (k₂⋅x - ω₂⋅t) som reser med olika hastigheter v₁= Ω₁/k₁ och v₂= Ω₂/k₂. Observera hur grupphastigheten skiljer sig från fashastigheten, i detta fall är grupphastigheten ∆ω/∆k.

Det kan tjäna dig: Magnetiska egenskaper hos material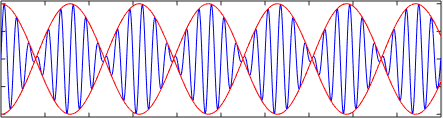Linjär (blå) våg i ett spridande medium. Den röda kurvan har lagts till för att markera att grupphastigheten skiljer sig från förökningshastigheten

Beroende på spridningsförhållandet kan fashastigheten och grupphastigheten i motsatta riktningar till och med ha motsatta riktningar.

Exempel på linjära vågor

Elektromagnetiska vågor

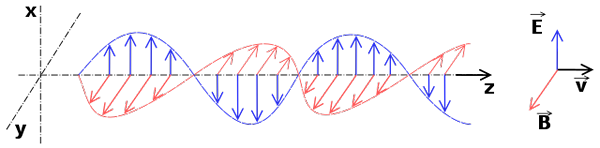elektromagnetiska vågor som utgör elektromagnetisk strålning

Elektromagnetiska vågor är linjära vågor. Dess vågekvation härleds från ekvationerna för elektromagnetism (Maxwell -ekvationer) som också är linjära.

Schrödingers ekvation

Det är ekvationen som beskriver dynamiken hos partiklarna i atomskalan, där de böljande egenskaperna är relevanta, till exempel fallet med elektroner i atomen.

Sedan är "elektronvågen" eller vågfunktionen som den också kallas en linjär våg.

Vågor i djupt vatten

Linjära vågor är också de där amplituden är mycket lägre än våglängden och våglängden mycket större än djupet. Vågorna i djupt vatten följer den linjära teorin (känd som Airys böljande teori).

Men vågen som närmar sig stranden och bildar den karakteristiska vapen som rullas (och som surfare älskar) är en icke -linjär våg.

Ljud

Eftersom ljud är en liten störning av atmosfärstrycket, betraktas det som en linjär våg. Chockvågen av en explosion eller vågfront i ett supersoniskt plan är dock typiska icke -linjära vågexempel.

Vågor på ett spänt rep

Vågorna som sprids genom ett spänt rep är linjära, förutsatt att den initiala pulsationen är liten, det vill säga den elastiska gränsen för repet överskrids inte.

Linjära vågor på strängarna återspeglas vid deras ändar och överlappar varandra, vilket ger upphov till stationära vågor eller vibrationslägen som ger de harmoniska och subarmoniska tonerna som är karakteristiska för stränginstrument.

Referenser

1. Griffiths G och Schiesser W. Linjära och olinjära vågor. Återhämtad från: sholarpedia.org.
2. Whitham G.B. (1999) "Linjära och olinjära vågor". Wiley. 
3. Wikipedia. Icke -linjära vågor. Återhämtad från: är.Wikipedia.com
4. Wikipedia. Olinjär akustisk. Hämtad från: i.Wikipedia.com
5. Wikipedia. Vågor. Hämtad från: i.Wikipedia.com
6. Wikiwaves. Olinjära vågor. Återhämtat sig från: wikiwaves.org