Fourier Series -applikationer, exempel och övningar löst

De Fourier-serier De består av en summa av oändliga termer, som består av harmoniska funktioner, sinus och kosinus, vars argument är en hel grundläggande av en grundläggande frekvens.

Sinus- och kosinusfunktionerna multipliceras med värden -koefficienter, så att summan är identisk med en funktion med period T lika med två gånger Pi (2π) dividerat med den grundläggande vinkelfrekvensen ω ω Ω Ω.

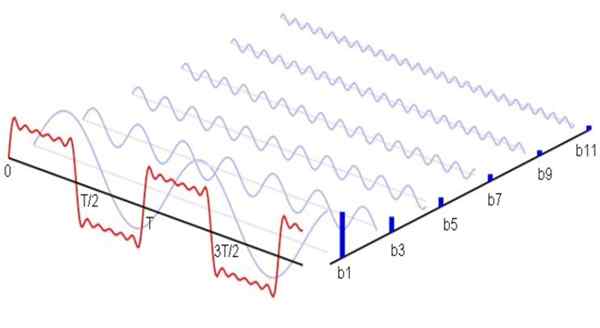
Figur 1. Här är (i blått) de första icke -nollharmonikerna i Fourier -serien som motsvarar en fyrkantig vågformsignal. Summan dessa harmonier ger upphov till den röda signalen. Källa: Wikimedia Commons.

Matematiskt skulle det uttryckas på följande sätt: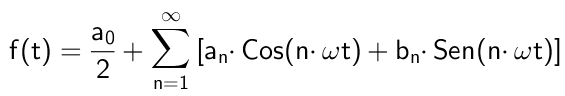

Var Ω Det är den grundläggande frekvensen, som är relaterad till perioden T av funktionen med) Genom förhållandet: 

Ω = 2π / t

För att vara periodisk period T, funktionen med) uppfyller detta tillstånd:

f (t) = f (t + k t)

Var k Det är ett heltal och koefficienterna till₀ , till_n och b_n De kallas Fourier -koefficienter.

[TOC]

Betydelse och användning av Fourier -serier

Namnet på Fourier -serien beror på att hans upptäckare var den franska matematiska.

Denna upptäckt var grundläggande för matematik, eftersom om en differentiell ekvation har en viss harmonisk lösning, är det möjligt att uppnå den allmänna lösningen med hjälp av överlappningen eller summan av samma.

Fouriers koefficienter för en periodisk funktion, även kallad skylt, De är spektrumet av detsamma.

Därför är spektrumet uppsättningen frekvenser som utgör en signal som kännetecknas av amplituden för varje frekvens, vilket motsvarar värdena på Fouriers koefficienter.

Signalkomprimeringssystem eller ljud- och videovågformer, i ryggen betydligt mindre antal bitar än den ursprungliga digitaliserade signalen.

Fourier -serien med en signal är som dess fingeravtryck, i den meningen att du, kända koefficienterna som utgör det, kan du alltid veta vilket tecken de hör hemma.

Även om användningen av Fourier -serien, eller dess mest allmänna form, Fouriertransform, Som en signalkomprimeringsmetod har det varit känt länge, dess användning i praktiken var tvungen att vänta på numeriska processorer tillräckligt snabba, vilket gjorde att signalerna kunde komprimeras och dekomprimeras i "realtid".

Kan tjäna dig: statistiska variabler

Fourier -serieexempel 

Därefter ett exempel på f (t) -funktion och dess Fourier -serie.

Funktionen är:

 f (t) = 0 ja 0 ≤ t  < π y 1 si π ≤  t   < 2π

Och har motsvarande Fourier -serie som ges av:

f (t) = ½ - 2/π⋅se (t) - 2/(3π) ⋅se (3t) - 2/(5π) ⋅sen (5t) - 2/(7π) ⋅sen (7t) - ..

Följande figur visar funktionen och delvis summan av Fourier -serien:

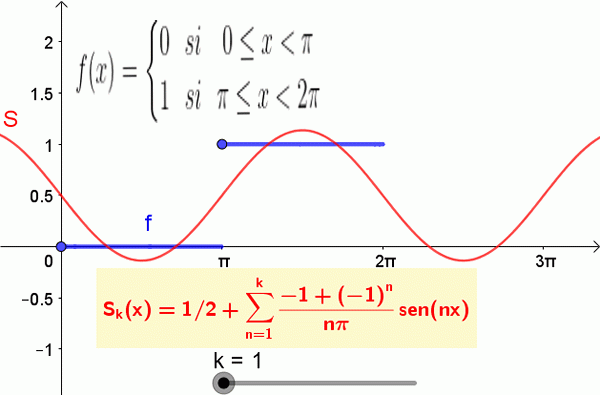figur 2. De första 19 termerna i Fouriers summa som motsvarar stegfunktionen visas. Källa: f. Zapata.

Bestämning av koefficienter

Nedan är hur man bestämmer Fouriers koefficienter:

Anta att funktionen är f (x) definierad i ett intervall som går från t_Yo till t_Yo + T, där kapitalet kommer att vara perioden för funktionen. Då är hans Fourier -serie:

f (t) = a₀/2 + a₁ cos (ω t) + a₂ cos (2 Ω t) + ... + a_n Cos (n ω t) +..

.. .+ B₁ sin (ω t) +b₂ sin (2 Ω t) +... +B_n Sin (n ω t) +..

Beräkning av den oberoende termen

För att hitta den oberoende termen integrerar vi båda jämställdhetsmedlemmarna i intervallet för definitionen av funktionen:

[t_Yo , t_Yo+ T]

Därför:

Samma_n ∫cos (n ω t) dt +..

.. .+ B₁ ∫sen (Ω t) dt +b₂ ∫sen (2 Ω t) dt +... +b_n ∫sen (n ω t) dt +..

Här betyder symbolen ∫ integrerad definierad från t_Yo till t_Yo + T.

Integrationen av den första termen är T, som vid utvärderas i dess övre gränsresultat:

t_Yo + T

När du subtraherar den nedre gränsen t_Yo, i definitiv t.

Alla andra termer är 0, eftersom det här är kosinus- eller sinusfunktioner utvärderade under en fullständig period, som vi visar nedan:

∫COS (NΩ T) DT = (1/ nΩ) ∫COS (NΩ T) D (NΩ T)

Kom ihåg att symbolen ∫ betyder integration mellan T_Yo till t_Yo + T. 

För att göra integrationen av termerna som har kosinus eller bröst kommer vi att göra följande ändring av variabel:

x = ω (t - t_Yo)

Så X, dx -skillnaden är lika med D (ωt) -skillnaden.

Så integralen som ska genomföras är:

Eftersom N är ett heltal kommer den definierade integralen alltid att ge noll. Detsamma gäller för sinusfunktionen.

Därför innehåller den definierade integralen utvärderad i en fullständig period av alla termer. 

Kan tjäna dig: divisioner där återstoden är 300

Det dras därför slutsatsen att termen A₀ beräknas enligt följande:

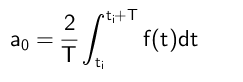
Beräkning av koefficienter till

För att beräkna koefficienterna till de som multiplicerar till kosinusfunktionerna måste båda jämställdhetsmedlemmarna multipliceras:

f (t) = a₀/2 + a₁ cos (ω t) + a₂ cos (2 Ω t) + ... + a_n Cos (n ω t) +..

.. .+ B₁ sin (ω t) +b₂ sin (2 Ω t) +... +B_n Sin (n ω t) +..

Genom kosinusfunktionen utvärderas i motsvarande harmonik och sedan tillämpas den integrerade i en fullständig period till båda medlemmarna. 

Till exempel för att beräkna_m Båda medlemmarna multipliceras med COS (MΩT):

f (t) cos (m ω t) = a₀/2 cos (m ω t) + a₁ cos (ω t) cos (m ω t) + a₂ cos (2 Ω t) cos (m ω t) + ... + till_n Cos (n ω t) cos (m ω t) +..

.. .+ B₁ sin (ω t) cos (m ω t) +b₂ sin (2 Ω t) cos (m ω t) +... +b_n Sin (n ω t) cos (m ω t) +..

Integreras sedan i en komplett period, det vill säga i intervallet som går från t_Yo till t_Yo + T.

Integrationen av termen som innehåller A₀ avbryts, eftersom M är ett heltal och kosinusfunktionen integreras i en fullständig period. 

Integraler som innehåller produkten cos (n ω t) cos (m ω t) upphävs också när n ≠ m. Endast i fallet att n = m har integralen:

Alla termer som har en kosinus multiplicerad sinus, det vill säga de som multipliceras av B: s koefficienter, som innehåller integraler av SEN -typen (n ω t) cos (m ω t) avbryts när den definierade integralen görs på en fullständig period. 

Härifrån dras slutsatsen att:

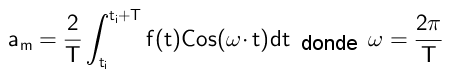
Beräkning av koefficienterna B: er

För att hitta B: s koefficienter tillämpas en liknande procedur, men den här gången multipliceras båda medlemmarna i funktionen till Fourier -serien med SEN -funktionen (M Ω T).

Av samma skäl som redan förklarats för fallet där den enda termen som inte upphävs efter att ha integrerats i en fullständig period är en där:

n = m

Och där integralen av [sen (m ω t)] visas]², som integreras under en fullständig period resulterar i π.

Kan tjäna dig: Homografisk funktion: Hur man graferar, löste övningar

På detta sätt beräknas B: s koefficienter enligt följande formel:

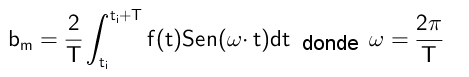
Övningar

- Övning 1

Gör den uttryckliga beräkningen av funktionen för koefficienterna

 f (t) = 0 ja 0 ≤ t  < π y 1 si π ≤  t   < 2π

Lösning

Först identifierar vi perioden t för denna funktion som 2π, så den grundläggande frekvensen ω = 2π/ t i detta exempel är lika med enheten, det vill säga:

Ω = 1

Funktionen definieras i intervallet [0, 2π], så alla integrationer kommer att utföras i nämnda intervall. 

Sedan beräknas den oberoende termen enligt följande:

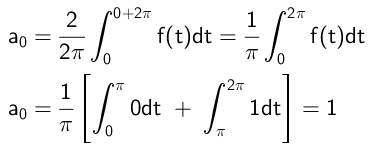
Koefficienterna som multiplicerar till kosinusfunktionerna beräknas på detta sätt:

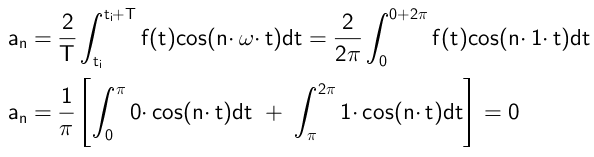
Som framgår är alla koefficienter till noll, vilket kommer att hända förutsatt att funktionen f (t) är udda.

På liknande sätt kommer B: s koefficienter att beräknas enligt följande:

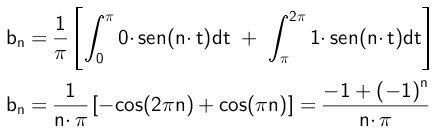
- Övning 2

Hitta koefficienterna för funktionen som motsvarar figur 1, vilket är:

f (t) = -1 ja 0≤ t

Lösning 

Eftersom funktionen tar värden mellan -1 och +1 kan vi intuitera att den oberoende termen är ogiltig, men vi kommer uttryckligen att beräkna den:

På grund av det faktum att funktionen har udda symmetri, måste alla koefficienter till de som multiplicerar de harmoniska termerna med kosinusfunktionen ogiltig. Vi verifierar det nedan:

Slutligen hittar vi B: s koefficienter som multiplicerar de harmoniska termerna som innehåller sinusfunktionen:

Var kan alla B: s villkor med UP -abonnemang märks är 0. De första udda termerna är:

b₁= -4/(π); b₃= -4/(3π); b₅= -4/(5π); b₇= -4/(7π) och B₉= -4/(9π)

https: // youtu.Vara/737yagwszya

Referenser

1. Amerror, jag. 2013. Behärskning av den diskreta Fourier -omvandlingen i en, två eller flera dimensioner: fallgropar och artefakter. Springer Science & Business Media.
2. Briggs, w. nittonhundranittiofem. DFT: En ägarhandbok för den diskreta Fourier -transformen. Siam.
3. Chu, e. 2008. Diskreta och kontinuerliga Fourier -transformationer: analys, applikationer och snabba algoritmer. CRC Press.
4. Guoan BI, Yonghong Zeng. 2012. Transformer och snabba algoritmer för signalanalys och representationer. Springer Science & Business Media.
5. Sundararajan, D. 2003. Digital signalbehandling: teori och praktik.Världsvetenskaplig. 
6. Wikipedia. Fourier-serier. Återhämtad från: är.Wikipedia.com