Frekvensfördelning Hur man gör en tabell, exempel, träning

En Frekvensfördelning I statistik hänvisar den till trenden som följer de data som organiseras i grupper, kategorier eller klasser, när var och en tilldelas ett nummer som kallas frekvens, vilket indikerar hur många data det finns i varje grupp. 

Som regel observeras att dessa frekvenser distribueras runt en central grupp: den med det högsta antalet data.

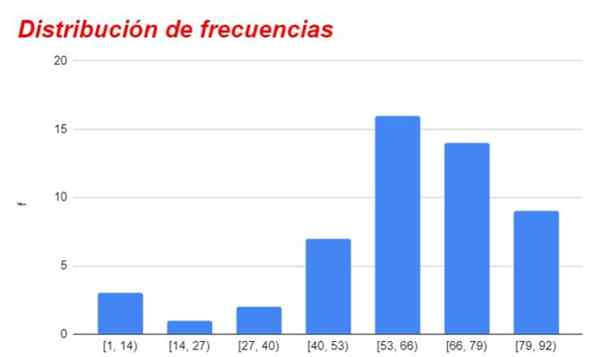
Figur 1. Frekvensfördelningsdiagrammet erhållet från motsvarande tabell. Källa: f. Zapata.

Grupper som är över eller under nämnda centrala kategori minskar gradvis sin frekvens, och är mycket små eller obetydliga för kategorierna längst från kategorin med en högre frekvens.

Vägen att känna till frekvensfördelningen för en datauppsättning består först för att skapa kategorierna och sedan göra frekvenstabellen. Den visuella representationen av frekvenstabellen kallas histogram.

[TOC]

Frekvenstyper

Det finns flera typer av frekvenser:

1.- Absolut frecuens: Det är den mest grundläggande, och från det är de andra byggda. Det består helt enkelt av det totala antalet data som motsvarar en kategori.

2.- Relativ frekvens: Det är den absoluta frekvensen för varje kategori dividerat med det totala antalet data.

3.- Procentuell frekvens: Det är samma relativa frekvens men multipliceras med hundra, vilket indikerar procentandelen värden utseende i varje kategori.

4.- Ackumulerad frekvens: Det är summan av de absoluta frekvenserna för kategorierna som är lägre eller lika med den kategori som övervägs. 

5.- Procentuell ackumulerad frekvens: Det är summan av procentuella frekvenser för kategorierna som är lägre eller lika med den kategori som observeras.

Steg för att göra en frekvensfördelningstabell

Det finns flera steg som ska följas för att bygga en frekvensfördelningstabell.

För det första måste data från ett träd etc.

Kan tjäna dig: vad är delarna av 30? (Förklaring)

Steg 1

Identifiera minsta värdet Xmin och det maximala värdet Xmax I datauppsättningen x.

Steg 2

Beräkna R -intervallet, som definieras som skillnaden mellan det maximala värdet mindre minimivärdet: r = xmax - xmin.

Steg 3

Bestämma numret k av intervaller eller klasser, som kan förhandas. Numret k kommer att bestämma antalet rader som frekvenstabellen kommer att ha.

Steg 4

Om antalet intervall k Det ges inte tidigare, då måste det fastställas enligt följande riktlinjer: det minsta antalet rekommenderade kategorier är 5, men det kan vara högre i vilket fall det är att föredra att välja ett udda nummer.

Steg 5

Det finns en formel som heter Sturgregel som ger oss antalet intervall k rekommenderas för en uppsättning som består av N data:

K = [1 + 3,322⋅Log n]

Som resultat inom konsolen säkert kommer att vara ett riktigt nummer, indikerar konsolen att det måste avrundas till det närmaste udda heltalet för att få ett heltalsvärde på k.

Steg 6

Amplituden beräknas TILL av varje intervall (klasser eller kategorier) som tar kvoten mellan intervallet R och antalet intervall k: A = r/k. Om de ursprungliga uppgifterna är hela siffrorna, är det närmaste heltalet avrundat, annars är dess verkliga värde kvar.

Steg 7

Bestäm de nedre och övre gränserna för varje intervall eller klass. Det första intervallet, eller den lägsta klassen, har som sin nedre gräns den minsta av originaldata, det vill säga li = xmin och som den övre gränsen minsta värdet plus amplituden för intervallet, är detta ls = xmin + a. 

Steg 8

De på varandra följande intervallen är: 

[Xmin, xmin + a), [ Xmin + a, xmin + 2⋅a), ... [ Xmin + (K-1) A, Xmin + K⋅A).

Kan tjäna dig: kombinerade operationer

Steg 9

XC -klassmärket bestäms för varje intervall med följande formel: Xc = (ls - li) / 2 + li.

Steg 10

Rubriken på frekvenstabellen placeras, som består av en rad med följande etiketter: klasser, XC -klassmärke, frekvens F, relativ frekvens F (eller procentuell frekvens F%) och ackumulerad frekvens F (eller ackumulerad procentuell frekvens F%).

Vad vi kommer att ha nästa är följande:

Första kolumnen i frekvensstabellen: innehåller intervall eller klasser där data har delats upp.

Andra kolumn: innehåller klassmärket (eller mellanliggande punkt) för varje underinterval.

Tredje kolumn: Innehåller den absoluta frekvensen f för varje klass eller kategori.

Fjärde och femte kolumn: Värdena som motsvarar den relativa (eller procentsatsen) frekvensen och den ackumulerade frekvensen F (eller procentuell ackumulerad) placeras.

Tabellkonstruktionsexempel

Följande data motsvarar de exakta svaren på 100 frågor som tillämpas på en grupp av 52 studenter:

65, 70, 70, 74, 61, 77, 85, 36, 70, 62, 62, 77, 80, 89, 39, 43, 70, 77, 79, 77, 88, 52, 85, 1, 55, 55, 47, 73, 63, 59, 51, 56, 65, 85, 79, 53, 79, 3, 71, 7, 54, 8, 61, 61, 77, 67, 58, 61, 45, 48, 64, 15, 50.

Vi kommer att följa stegen för att bygga frekvenstabellen:

1.- Minsta och maximala värden xmin = 1, xmax = 89.

2.- Intervallet är: r = 89 - 1 = 88

3.- Bestämning av antalet intervall enligt Sturgregel: K = [1 + 3 322⋅Log 52] = [6,70] = 7.

4.- Beräkning av intervallens bredd: A = R / K = 88/7 = 12,57 ≈ 13.

5.- Intervallerna är: [1,14), [14, 27), [27, 40), [40, 53), [53, 66), [66, 79), [79, 92).

6.- Klassmärkena för varje intervall bestäms: 8, 21, 34, 47, 60, 73 och 86.

7.- Tabellen är gjord:

Kan tjäna dig: interna och externa konjugatvinklar: exempel, övningar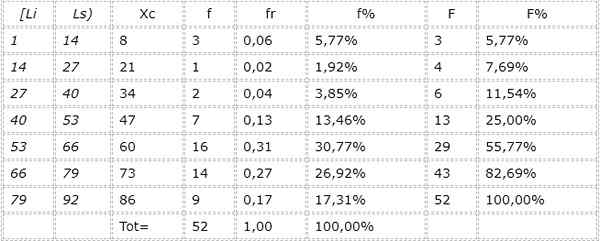

Grafen över frekvenserna för olika intervall eller kategorier visas i figur 1.

Träning löst

En lärare registrerar andelen mål som uppnåtts i ämnet fysik för varje elev. Kvalificeringen till varje student, även om den beror på andelen mål som uppnåtts, är dock tät för vissa kategorier som tidigare fastställts i universitetsstudiernas förordningar.

Låt oss titta på ett specifikt fall: I ett fysikavsnitt har du procentandelen av mål som uppnåtts för var och en av de 52 studenterna: 

15, 50, 62, 58, 51, 61, 62, 74, 65, 79, 59, 56, 77, 8, 55, 70, 7, 36, 79, 61, 77, 52, 35, 43, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61. 65, 70, 89, 64, 54, 85, 61, 39, 63, 70, 85, 70, 79, 48, 77, 73, 67, 45, 77, 71, 53, 88, 85, 47, 73, 77, 80.

I det här exemplet motsvarar kategorierna eller klasserna den slutliga kvalifikationen som tilldelats enligt procentandelen x av uppnådda mål:

1.- Mycket dålig: 1 ≤ x < 30

2.- Dålig: 30 ≤ x < 50

3.- Tillräckligt: ​​50 ≤ x < 70

4.- Tja: 70 ≤ x < 85

5.- Utmärkt: 85 ≤ x ≤ 100

För att göra frekvenstabellen beställs data från minst till största och berättar hur många data som motsvarar varje kategori, vilket kommer att vara den kvalifikation som eleven kommer att få i ämnet fysik:

1.- Mycket fattiga: 4 studenter.

2.- Dålig: 6 studenter.

3.- Tillräckligt: ​​20 studenter.

4.- Tja: 17 studenter.

5.- Utmärkt: 5 studenter.

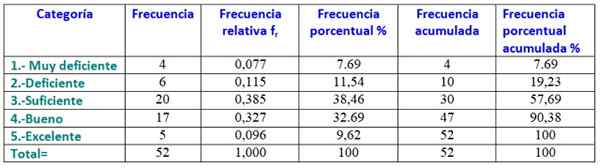
Nedan är histogrammet av betyg, byggt från föregående tabell:

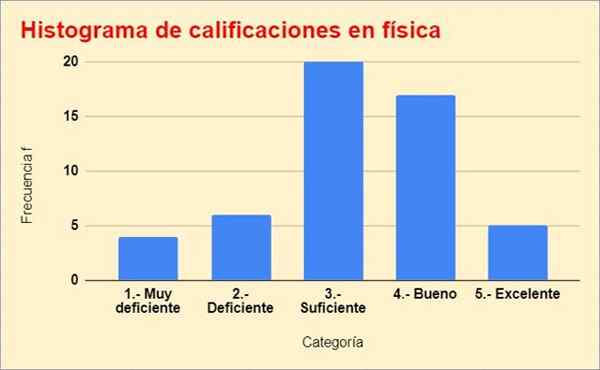figur 2. Frekvensfördelningsgrafen för övningen löst. Källa: f. Zapata.

Referenser

1. BERENSON, M. 1985. Statistik för administration och ekonomi. Inter -American S.TILL.
2. Canavos, g. 1988. Sannolikhet och statistik: Tillämpningar och metoder. McGraw Hill.
3. Devore, j. 2012. Sannolikhet och statistik för teknik och vetenskap. 8th. Utgåva. Häck.
4. Levin, r. 1988. Statistik för administratörer. 2: a. Utgåva. Prentice hall.
5. Spiegel, m. 2009. Statistik. Schaumserie. 4 TA. Utgåva. McGraw Hill.
6. Walpole, r. 2007. Sannolikhet och statistik för teknik och vetenskap. Pearson.