Matematik

Rektangulärt koordinatsystem

Rektangulärt koordinatsystem
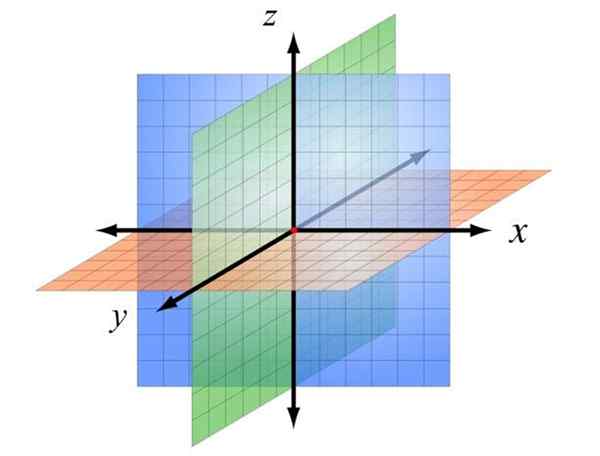
Cartesian koordinatsystem i tre dimensioner. Källa: Wikimedia Commons

Vad är det rektangulära koordinatsystemet?

I matematik och geometri, a rektangulärt koordinatsystem Det tjänar till att exakt hitta någon punkt på rymden. För detta räcker det för att ge tre koordinater.

Konstruktionen av systemet i planet är mycket enkelt, endast tre linjer som kommer att vara koordinataxlarna eller kartesiska axlar behövs: en vertikal, en annan horisontell och en tredjedel som kommer in eller lämnar papperet eller skärmen.

Dessa axlar är ömsesidigt vinkelräta och skärningspunkten är ursprung av systemet.

Denna bestämmelse visas i figuren ovan, där bokstäverna har tilldelats bokstäverna x, och, z, att skilja dem. På detta sätt bestäms tre plan, med ursprunget färgat i rött.

Planet Xz, I blått är det skärmens plan och är framför läsarens ögon. Planet Xy Den är orange och kan associeras med bordet eller golvet. Slutligen planet zy I grönt är det vinkelrätt mot de tidigare och sektionen skärmen eller papperet i två regioner.

Fyrkantig var och en av dessa plan och tilldela en skala kan du placera vilken punkt som helst i rymden som ger respektive koordinater X och z, Alltid i den ordningen, för att undvika oklarheter.

För vadDet tjänar det rektangulära koordinatsystemet?

Det rektangulära koordinatsystemet tjänar till att placera vilken punkt som helst i rymden eller i planet, tillräckligt för att indikera de tre koordinaterna för punkten, i ordning x, y, z.

Det kan tjäna dig: nominell variabel: koncept och exempel

Om punkten tillhör ett plan kommer en av koordinaterna att vara 0 och om den är på någon av axlarna kommer två av koordinaterna att vara 0, förutom att motsvarande platsen för punkten, utom ursprunget, som, som, som Sade tidigare, har koordinater (0,0,0).

Följande exempel klargör ovanstående.

Exempel

Exempel 1

En vilken punkt P på X -axeln uttrycks genom koordinater P (X, 0, 0). Observera att ursprunget, som markeras i rött i följande figur, har koordinater eller (0, 0, 0).

När poängen är till höger om ursprunget har den positiv X -koordinat, medan om den är till vänster är den negativ. Till exempel har P1 Blue Point koordinater (6,0,0), medan punkt P2 i grönt, har koordinater (-9,0,0).

Exempel 2

I följande figur finns det två axlar, som är X -axel den horisontella axeln och Axel y Vertikal. Med detta räcker det för att representera punkter i planet, två koordinater är nödvändiga. Ursprunget eller är poängen (0,0).

Observera att dispositionen av axlarna delar upp planet i fyra regioner som kallas kvadranter. Axlarna ovanför och till höger om ursprunget betecknas med ett positivt tecken, medan nedan och till vänster är de utmärkta med ett negativt tecken.

Sedan motsvarar de punkter vars koordinater är positiva båda den första kvadranten eller kvadranten i. Green Point har koordinater (2,3) och är i I -kvadranten.

För sin del har den röda punkten koordinater (-3,1) och är i II-kvadranten, medan koordinaterna för den blå punkten är (-1.5; -2.5) och det är i III -kvadranten.

Kan tjäna dig: Vanlig faktorisering: Exempel och övningar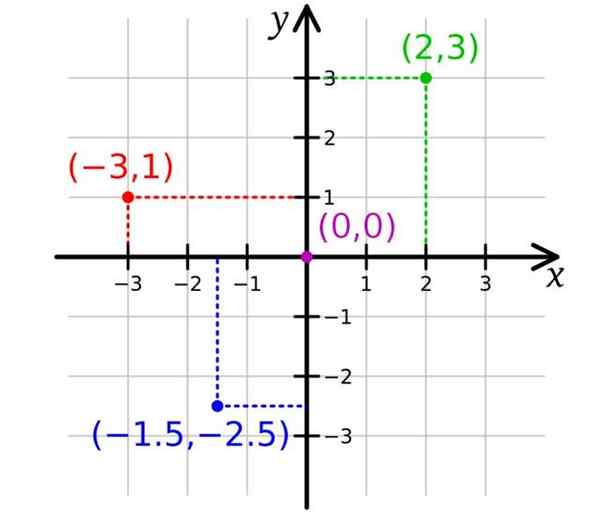 Kartesist. Källa: Wikimedia Commons

Exempel 3

Följande är ett exempel på en punkt i rymden. Dess koordinater är x = 6, y = 10 och z = 8, därför p (6,10,8).

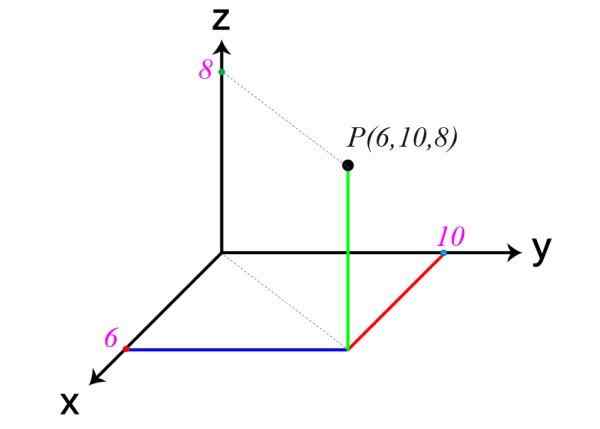Ett annat exempel på kartesiska axlar

I början av början varnas det att planerna XY, XZ och ZY delar upp utrymmet i åtta regioner, kallade Oärter. Exemplet P är i den första ocanten.

Referenser

  1. Alexander, D. (2013). Geometri. Femte. Utgåva. Cengage Learning.
  2. Larson, r. (2012). Förkalkning. 8th. Utgåva. Cengage Learning.
  3. Stewart, J. (2007). Preccculment: Matematik för beräkning. Femte. Utgåva. Cengage Learning.
  4. Det kartesiska planet. Hämtad från: DL.Obehandlad.Edu.
  5. Weisstein, E. Kartesiska koordinater. Återhämtat sig från: Mathworld.Volfram.com