Sammansättning

Succession bestående av gula och blå rutor. Källa: f. Zapata

Vad är en sammansatt följd?

En sammansättning Den består av en sekvens av element, skapad från två (eller mer) olika och alternativa efterföljningar. Var och en av dessa efterföljningar har en viss regel, som används för att hitta sina respektive element.

Elementen behöver inte vara numeriska, att kunna vara figurer, symboler eller bokstäver, men de som är baserade på siffror kallas aritmetiska successioner. Den figur som vår artikel börjar visar en sammansatt arv från gula och blå rutor.

I denna arv börjar det från en stor fyrkant som består av 8 gula rutor och en blå fyrkant. För att få följande termin läggs en gul kvadrat till vänster eller höger om den första och tredje raden med rutor. Utrymmet som resulterar i den centrala raden är fylld med en blå fyrkant.

Varje figur i sekvensen kallas termin. Om du vill hitta den femte terminen måste du lägga till en gul fyrkant till höger om de första och tredje rankningarna och en blå kvadrat i den andra raden:

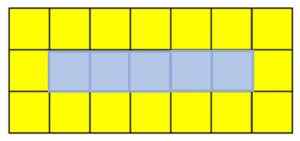Femte termin av en följd av gula och blå rutor. Källa: f. Zapata

Förklaring

I sammansatta successioner erhålls termerna genom att växla villkoren för två eller flera oberoende enkla successioner. För att bättre förstå idén bör den granskas detaljerna om en enkel följd.

Till exempel består följande enkla succession av de naturliga siffrorna:

2, 4, 6, 8, 10, 12 ..

De suspensiva punkterna indikerar att successionen har oändliga termer.

Var och en av villkoren betecknas med ett litet brev och ett nummer, som ett abonnemang. Detta nummer indikerar positionen eller index av varje termin. I föregående succession kan du skriva:

till₁ = 2; till₂ = 4; till₃ = 6; till₄ = 8 ..

Det är mycket bekvämt att ha ett sätt att beräkna alla termer som är önskvärda av successionen, det vill säga dess speciella regel. Med henne N-Ésimo-termin, antingen Generalperiod, betecknas som en_n.

Kan tjäna dig: Egenskaper för jämlikhet

Fortsätter med exemplet med jämnt siffror, kan du fastställa sättet att beräkna termen n-Ésimo, från föregående termin:

till_n = a_N-1 + 2

Vart man ska_N-1 Det är termen som föregår_n.

Naturligtvis skulle det vara bättre att känna till den allmänna termen utan att bero på andra termer. I denna följd är det lätt att notera att varje term multiplicerar med 2 den position den upptar, med tanke på underskriften av termen. På detta sätt skrivs det:

till_n = 2n

De gamla grekerna visste redan efterföljningarna med jämna och udda siffror. Successionen av udda naturliga siffror kan under tiden skrivas som:

1, 3, 5, 7, 9, 11 ..

Och att kombinera följd av jämna siffrorna med det för det udda, är följande sammansatt succession:

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 ..

Vars resultat är uppsättningen av naturliga siffror.

Villkor för en sammansatt succession

Det kan vara kul att försöka hitta förhållandet som finns i en sekvens av siffror, för vilket det måste observeras noggrant och försöka identifiera om det är en sammansatt följd.

Den allmänna formen av en succession som består av två successioner kommer att vara:

till₁, b₁, till₂, b₂, till₃, b₃, till₄, b₄,..

Vart man ska₁, till₂, till₃, till₄,... är villkoren för den första successionen och b₁, b₂, b₃, b₄,... de andra. De är alltid isär, som är fallet i detta exempel:

7, 8, 14, 16, tjugoett, 24, 28, 32, 35..

Vad kommer att vara termen som följer?

För att veta, känna till följd i två alternativa uppsättningar av siffror, enligt följande:

• 7, 14, 21, 28, 35 ..
• 8, 16, 24, 32 ..

I den första av dessa uppsättningar visas multiplarna på 7:

till₁ = 7 × 1 = 7; till₂ = 7 × 2 = 14; till₃ = 7 × 3 = 21; till₄ = 7 × 4 = 28; till₅ = 7 × 5 = 35

Den allmänna termen för denna arv är:

till_n = 7n

Och i det andra är det multiplarna på 8:

b₁ = 8 × 1 = 8; b₂ = 8 × 2 = 16; b₃ = 8 × 3 = 24; b₄ = 8 × 4 = 32

Så dess allmänna term är:

Det kan tjäna dig: verklig verklig variabel funktion och dess grafiska representation

b_n = 8n

Återvända till den ursprungliga sammansättningen, tillhör 35 den första sekvensen, vars termer är att₁, till₂, till₃, till₄ ... 35 är den femte terminen, så termen som följer måste vara b₅, som lätt erhålls från regeln för att hitta den allmänna termen:

b₅ = 8 × 5 = 40

Och det är skrivet:

7, 8, 14, 16, tjugoett, 24, 28, 32, 35, 40 ..

Exempel på sammansatta efterföljningar

Exempel 1

Du kan skapa en sammansatt följd med geometriska figurer, till exempel torget och cirkeln, ordna dem som visas nedan:

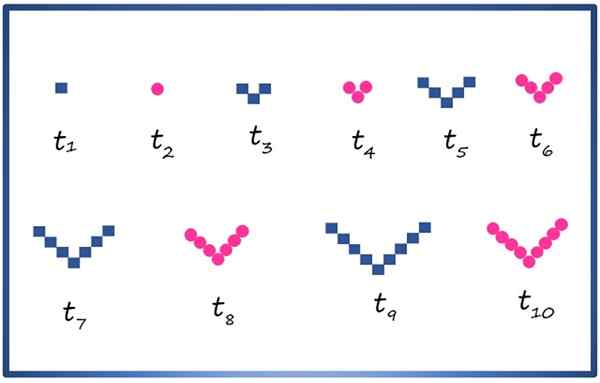De första tio termerna för en sammansatt succession med de fyrkantiga geometriska elementen och cirklar. Källa: f. Zapata

Varje term betecknas med t₁, t₂, t₃, t₄ ..., villkoren för Parque Index består av cirklar och de med udda index, rutor. Att noggrant observera sekvensen är det möjligt att till exempel veta att termen t_elva, som inte visas i bilden, består av 11 rutor med tillhandahållandet i v.

Exempel 2

Följande sammansatt succession består av symboler, i detta fall bokstäverna R och S:

R SS RR SSS RRR SSS RRRR SSSS RRRR SSSSS ..

Varje ny term byggs genom att lägga till ett brev till föregående. De första fyra termerna i den visade sekvensen är:

t₁= R ; t₂= H.h ; t₃= Rr ; t₄= Sss ..

Och nästa termin som skulle visas efter att de visade termerna är:

t_elva= Rrrrrr

Exempel 3

De föregående exemplen visade stigande successioner, där varje värde ökar på något sätt med avseende på det föregående. Men det behöver inte alltid vara på detta sätt, eftersom successionerna kan vara fallande, det vill säga de har ett minskningsmönster.

Och stigande successioner kan kombineras med fallande successioner.

Följande numerisk succession består:

4, 36, 7, 35, 10, ___, ___, 33, 16, ___, ___, ..

Det kan delas upp i två successioner:

• 4, 7, 10, ___, 16, ___, ..
• 36, 35, ___, 33, ___, ..

Vilka är värdena som måste placeras i de tomma utrymmena?

Om du noggrant observerar den första successionen erhålls varje term genom att lägga till 3 till föregående term. Det är därför en stigande succession:

Kan tjäna dig: vinkelförskjutning

7 = 4 + 3

10 = 7 + 3

Därför måste du i det första tomma utrymmet placera:

10 + 3 = 13

Efter detta är följande termin, i själva verket:

16 = 13 + 3

Och den som går i det andra blanketten är:

16 + 3 = 19

Den andra successionen är fallande och det är mycket lätt att hitta de saknade termerna, eftersom det observeras att varje term erhålls genom att subtrahera 1 från föregående termin, därför:

36, 35, 3. 4, 33, 32..

Slutligen kan du skriva:

4, 36, 7, 35, 10, 3. 4, 13, 33, 16, 32, 19,..

Löst övningar

Övning 1

I successionen består av exempel 3 i föregående avsnitt:

a) Tillhör 29 nämnda succession?

b) Skriv ytterligare 10 termer av denna succession

Svara på

Ja, det hör till, eftersom den andra successionen faller ner och dess villkor erhålls genom att subtrahera 1 från föregående termin. På detta sätt når det så småningom 29.

Svar B

4, 36, 7, 35, 10, 34, 13, 33, 16, 32, 19, 31, 22, 25, 29, 28, 31, 27, 34, ..

Observera att vissa termer upprepas.

Övning 2

Hitta de saknade termerna i följande föreningssekvens:

100, 500, 115, 480, 130, 460, 145, 440, 160, 420, ..

Svar

De udda termerna är skrivna för att få den första successionen:

100, 115, 130, 145, 160, ..

Det observeras att för att hitta varje term måste du lägga till 15 till föregående termin, därför är termen som följer vid 160 175 175.

Den andra successionen består av:

500, 480, 460, 440, 420, ..

Varje term skiljer sig från den föregående till 20, efterföljande är fallet, därför är termen som följs vid 420 400 är 400.

Med denna information läggs ytterligare två termer till den ursprungliga sammansättningen, så här:

100, 500, 115, 480, 130, 460, 145, 440, 160, 420, 175, 400, ..

Referenser

1. Larson, r. (2012). Förkalkning. 8th. Utgåva. Cengage Learning.
2. Stewart, J. (2007). Preccculment: Matematik för beräkning. Femte. Utgåva. Cengage Learning.
3. Sammansatta efterföljningar. Återhämtat sig från: media.EducacionCampeche.Gabb.mx.
4. Numeriska efterföljningar. Hämtad från: Matemathweb.com.
5. Efterföljningar. Aritmetiska och geometriska framsteg. Hämtad från: MacMillaneducation.är.