Summan av polynomer, som görs, exempel, övningar

De Summan av polynom Det är operationen som består av att lägga till två eller flera polynom, vilket resulterar i ett annat polynom. För att genomföra det är det nödvändigt att lägga till villkoren i samma ordning för var och en av polynomerna och ange den resulterande summan.

Först granskar vi kort betydelsen av "Villkor för samma ordning". En någons polynom består av summor och/eller subtraktion av termer.

Figur 1. För att lägga till två polynom är det nödvändigt att beställa dem och sedan minska liknande termer. Källa: Pixabay + Wikimedia Commons.

Villkoren kan vara produkter med verkliga nummer och en eller flera variabler, representerade med bokstäver, till exempel: 3x² och -√5.till²före Kristus³ De är villkor.

Tja, villkoren för samma ordning är de som har samma exponent eller kraft, även om de kan ha olika koefficient.

-Villkor för lika ordning är: 5x³, √2 x³ och -1/2x³

-Olika beställningsvillkor: -2x^-2, 2xy^-1 och √6x²och

Det är viktigt att komma ihåg att endast villkoren för samma ordning kan läggas till eller subtraheras, en operation som är känd som minskning. Annars är summan helt enkelt angiven.

När begreppet villkor för samma ordning klargörs, läggs polynomerna till dessa steg:

-Beställa Först polynomerna att lägga till, allt på samma sätt, antingen ökar eller minskar, det vill säga med makterna från minst till största eller vice versa.

-Att slutföra, Om någon kraft i sekvensen saknas.

-Minska Liknande termer.

-Ange Den resulterande summan.

[TOC]

Polynomsumma exempel

Vi börjar med att lägga till två polynomer med en enda variabel som heter x, till exempel polynomerna p (x) och q (x) som ges av:

P (x) = 2x² - 5x⁴ + 2x -x⁵ - 3x³ +12

Q (x) = x⁵- 25 x + x²

Efter de beskrivna stegen börjar det med att beställa dem minskat, vilket är det vanligaste sättet:

P (x) = -x⁵- 5x⁴  - 3x³  + 2x² + 2x +12

Det kan tjäna dig: inskriven vinkel i en cirkel: definition, sats, exempel

Q (x) = x⁵+ x² - 25x

Polynom Q (x) är inte komplett, det ser att krafter med exponent 4, 3 och 0. Det senare är helt enkelt den oberoende termen, den som inte har något brev.

Q (x) = x⁵+ 0x⁴ + 0x³ + x² - 25x + 0

När detta steg är gjort är de redo att lägga till. Du kan lägga till liknande termer och sedan ange summan, eller placera polynomerna som beställs av varandra och minska med kolumner på detta sätt:

- x⁵ - 5x⁴  - 3x³ + 2x² + 2x +12

+ x⁵ + 0x⁴ + 0x³  +  x²  - 25x + 0     +

--

0x⁵-5x⁴ - 3x³  +3x² - 23x + 12 = p (x) + q (x)

Det är viktigt att notera att när det läggs till, görs det algebraiskt med att respektera teckenregeln, på detta sätt 2x + (-25 x) = -23x. Det vill säga om koefficienterna har olika tecken subtraheras och resultatet bär tecknet på det stora.

Lägg till två eller flera polynomer med mer än en variabel

När det gäller polynom med mer än en variabel väljs en av dem för att beställa den. Anta till exempel att det uppmanas att lägga till:

R (x, y) = 5x²  - 4y² +  8xy - 6y³ 

OCH:

T (x, y) = ½ x²- 6y²  - 11xy + x³och

En av variablerna väljs, till exempel X att beställa:

R (x, y) = 5x² +  8xy - 6y³  - 4y²

T (x, y) = + x³y + ½ x² - 11xy - 6y² 

De saknade termerna är omedelbart slutförda, enligt vilka varje polynom har:

R (x, y) = 0x³och + 5x² +  8xy - 6y³  - 4y²

T (x, y) = + x³y + ½ x² - 11xy + 0y³ - 6y² 

Och båda är redo att minska liknande termer:

0x³och + 5x² +  8xy - 6y³  - 4y²

Kan tjäna dig: Bestämningskoefficient: Formler, beräkning, tolkning, exempel

+ x³y + ½ x² - 11xy + 0y³ - 6y²       +

-

+ x³Y + 11/2x² - 3xy - 6y³  - 10y²    = R (x, y) + t (x, y)

Polynomiska summanövningar

- Övning 1

I nästa summa av polynom, ange termen som måste gå i tomt för att erhålla polynomsumman:

-5x⁴  + 0x³ +  2x²         + 1

x⁵  + 2x⁴             - 21x² + 8x - 3

2x⁵             +9x³             -14x

-

-6x⁵+10x⁴ -0x³  + 5x²   - 11x + 21

Lösning

För att få -6x⁵ En term på axelformen krävs⁵, Så att:

A + 1+ 2 = -6

Därför:

A = -6-1-2 = -9

Och termen eftertraktad är:

-9x⁵

-Fortsätt på liknande sätt för att hitta resten av villkoren. Här är exponent 4:

-5 + 2 + A = 10 → A = 10 + 5-2 = 13

Den saknade termen är: 13x⁴.

-För x krafter³ Det är omedelbart att termen måste vara -9x³, På detta sätt är den kubikterminskoefficienten 0.

-När det gäller fyrkantiga krafter: A + 8 -14 = -11 → A = -11 -8 + 14 = -5 och termen är -5x².

-Den linjära termen erhålls av A +8 -14 = -11 → A = -11 + 14 -8 = -5, är den saknade termen -5x.

-Slutligen är den oberoende termen: 1 -3 + a = -21 → a = -19.

- Övning 2

En platt terräng är omgiven som visas i figuren. Hitta ett uttryck för:

a) omkretsen och

b) dess område, i termer av de angivna längderna:

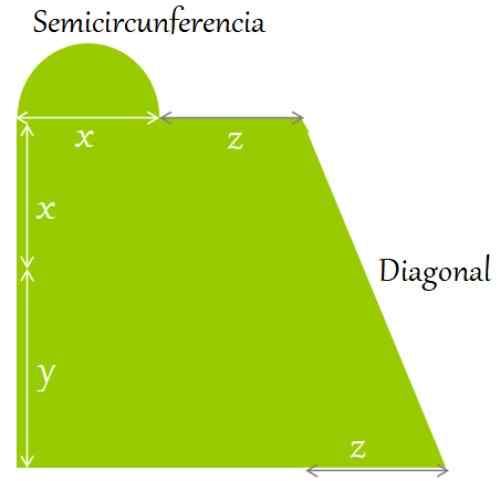figur 2. En platt terräng är omgiven av den angivna formen och dimensioner. Källa: f. Zapata.

Lösning till

Omkretsen definieras som summan av figurens sidor och konturer. Börjar i det nedre vänstra hörnet, i riktning mot klockhänderna, har du:

Det kan tjäna dig: Isosceles Trapezoid: Egenskaper, relationer och formler, exempel

Omkrets = y + x + halvcirkellängd + z + diagonal + Z + z + x

Halvcirkeln har en diameter lika med x. Eftersom radien är halva diametern måste den:

Radio = x/2.

Formeln för längden på en fullständig omkrets är:

L = 2π x radio

Så:

Halvcirkellängd = ½. 2π (x/2) = πx/2

För sin del beräknas diagonalen med Pythagoras -satsen som appliceras på sidorna: (x+y) som är vertikal sida och z, som är horisontellt:

Diagonal = [(x+y)² + z²]^1/2

Dessa uttryck ersätts i omkretsen för att få:

Omkrets = y + x + πx/2 + z + [(x + y)² + z²]^1/2+ z + x + z

Liknande termer minskas, eftersom summan kräver att resultatet förenklas till maximalt:

Omkrets = y + [x + π (x/2) + x] + z + z + z + [(x + y)² + z²]^1/2 = y + (2 + π /2) x + 3z

Lösning B

Det resulterande området är summan av rektangelområdet, halvcirkeln och den högra triangeln. Formlerna för dessa områden är:

-Rektangel: Bas x höjd

-Halvcirkel: ½ π (radio)²

-Triangel: Bas x höjd /2

Rektangelområde

(x+y). (x+z) = x² + Xz + yx + yz

Halvcirkelområde

½ π (x/2)² = π x² / 8

Triangelområdet

½ z (x + y) = ½ zx + ½ zy

Totalarea

För att hitta det totala området läggs de uttryck som finns för varje partiellt område:

Totalt area = x² + Xz + yx + yz + (π x² / 8) + ½ zx + ½ zy

Och slutligen alla termer som liknar:

Totalt area = (1 + π/8) x² + 3/2 xy + 3/2yz + yx

Referenser

1. Baldor, a. 1991. Algebra. Venezuelan kulturell redaktion.TILL.
2. Jiménez, r. 2008. Algebra. Prentice hall.
3. Matematik är kul. Tillägg och subtraktionspolynomer. Återhämtat sig från: matematik.com.
4. Monterey Institute. Lägga till och subtrahera polynomer. Återhämtat sig från: MontereyInstitute.org.
5. UC Berkeley. Algebra av polynomer. Återhämtat sig från: matematik.Berkeley.Edu.