Teori om uppsättningar egenskaper, element, exempel, övningar

De inställningsteori Det är en gren av logikmatematiken som ansvarar för studien av förhållanden mellan enheter som kallas uppsättningar. Uppsättningarna kännetecknas av att vara samlingar av föremål av samma natur. Dessa objekt är elementen i uppsättningen och kan vara: siffror, bokstäver, geometriska figurer, ord som representerar föremål, föremålen själva och andra.

Det var Georg Cantor, mot slutet av 1800 -talet, som föreslog uppsättningen av uppsättningar. Medan andra anmärkningsvärda matematiker under det tjugonde århundradet gjorde sin formalisering: Gottlob Frege, Ernst Zermelo, Bertrand Russell, Adolf Fraenkel bland andra.

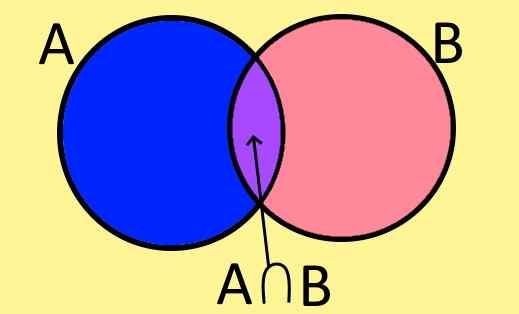
Figur 1. Venn -diagram över uppsättningar A, B och deras korsning A⋂ B. (Egen utarbetande).

Venn -diagram är det grafiska sättet att representera en uppsättning och består av en stängd platt figur inom vilken elementen i uppsättningen är.

Till exempel visar figur 1 två uppsättningar A och B, som har element gemensamt, elementen som är gemensamma för A och B. Dessa bildar en ny uppsättning som kallas skärningssatsen för A och B, som är skriven symboliskt enligt följande:

A ∩ B

[TOC]

Egenskaper

Uppsättningen är ett primitivt koncept som det är i geometri begreppet punkt, rak eller platt. Det finns inget bättre sätt att uttrycka konceptet än att påpeka exempel: 

Uppsättningen och bildas av färgerna på Spaniens flagga. Detta sätt att uttrycka uppsättningen kallas genom att förstå. Samma uppsättning och skriven av förlängningen är:

E = röd, gul

I detta fall är röda och gula element i uppsättningen och. Det bör noteras att elementen är listade mellan nycklarna och inte upprepas. När det gäller den spanska flaggan finns det tre ränder av färger (röd, gul, röd) varav två upprepas, men elementen upprepas inte när uppsättningen uttrycks.

Anta att Set V bildas av de tre första vokalbokstäverna:

V = a, e, i

Kraften hos V, som betecknas med P (V) är uppsättningen av alla uppsättningar som kan bildas med elementen i V:

P (v) = a, e, i, a, e, a, i, e, i, a, e, i

Typer av uppsättningar

Ändlig uppsättning

Det är en uppsättning där dess element är numrable. Exempel på ändliga uppsättningar är bokstäverna i det spanska alfabetet, spanska vokaler, planeterna i solsystemet bland andra. Antalet element i en ändlig uppsättning kallas dess kardinalitet.

Oändlig uppsättning

Oändlig ensemble, alla som numret på dess element är oöverträffligt, eftersom oavsett hur stort antalet av dess element alltid är möjligt att hitta fler element.

Ett oändligt uppsättningsexempel är uppsättningen av naturliga siffror n, som uttrycks i stor utsträckning på följande sätt:

Kan tjäna dig: Coplanares Points: Ekvation, exempel och lösta övningar

N = 1, 2, 3, 4, 5, .. . är helt klart en oändlig uppsättning, eftersom det inte spelar någon roll hur stort ett naturligt antal kan vara, följande major kan alltid hitta i en oändlig process. Det är uppenbart att kardinaliteten i en oändlig uppsättning är ∞.

Tomt uppsättning

Det är uppsättningen som inte innehåller något element. Den tomma uppsättningen V betecknas med Ø eller med hjälp av ett par nycklar utan element inuti:

V = = Ø.

Den tomma uppsättningen är unik, därför måste den vara felaktig att säga "en tom uppsättning", rätt form är att säga "den tomma uppsättningen".

Bland egenskaperna hos den tomma uppsättningen är det att det är undergruppen för alla uppsättningar:

Ø ⊂ a

Dessutom, om en uppsättning är delmängd av den tomma uppsättningen, kommer denna uppsättning nödvändigtvis att vara tomrummet:

A ⊂ Ø ⇔ A = Ø

Enhetlig uppsättning

Det kallas Unitary Set någon uppsättning som innehåller ett enda element. Till exempel är uppsättningen naturliga satelliter på jorden en enhetsuppsättning, vars enda element är månen. Ställ B av hela antal mindre än 2 och större än noll har endast element 1 därför är det en enhetsuppsättning.

Binär

En uppsättning är binär om den bara har två element. Till exempel set x, så att x är ett verkligt antal x^2 = 2 = 2. Denna uppsättning i förlängningen är skriven så här:

X = -√2, +√2

Universell uppsättning

Universal -uppsättningen är en uppsättning som innehåller andra uppsättningar av samma typ eller natur. Till exempel är den universella uppsättningen naturliga siffror uppsättningen av verkliga siffror. Men verkliga siffror är också universella av hela siffror och rationella siffror.

Kärnföremål

- Förhållanden mellan uppsättningarna

I uppsättningarna kan du etablera flera typer av förhållanden mellan dem och deras element. Om två uppsättningar A och B har exakt samma element, bland dem betecknas en lika relation enligt följande:

TILL = B

Om alla element i en uppsättning att tillhöra en uppsättning B, men inte alla element i B tillhör A, så finns det bland dessa uppsättningar ett inkluderingsförhållande som betecknas enligt följande:

A ⊂ B, men B ⊄ A

Det föregående uttrycket lyder: A är delmängd av B, men B är inte delmängd av en.

För att indikera att vissa eller vissa element tillhör en uppsättning används symbolen för tillhörighet ∈, till exempel för att säga att X -element eller element tillhör uppsättningen A är skrivet symboliskt enligt följande:

x ∈ A

Ja ett element och tillhör inte uppsättningen till detta förhållande skrivs så här:

och ∉ a

Det tillhörande förhållandet ges mellan elementen i en uppsättning och uppsättningen, med det enda undantaget från kraftuppsättningen, uppsättningen är insamlingen eller uppsättningen av alla möjliga uppsättningar som kan bildas med elementen i nämnda uppsättning.

Kan tjäna dig: faktorisering

Anta v = a, e, i, din kraft är p (v) = a, e, i, a, e, a, i, e, i, a, e, i, i så fall blir uppsättningen v ett element i uppsättningen p (v) och kan skrivas:

V ∈ P (V)

- Inkluderingsegenskaper

Den första egenskapen med inkludering konstaterar att varje uppsättning finns i sig själv, eller med andra ord, som är undergruppen av sig själv:

A ⊂ a

Den andra egenskapen med inkludering är transitivitet: om A är delmängd av B och B i sin tur är den delmängd av C, då är A delmängd av C. Symbelt skrivs transitivitetsförhållandet så här:

(A ⊂ B) ^ (B ⊂ C) => A ⊂ C

Nedan är Venn -diagrammet som motsvarar transitiviteten för inkludering:

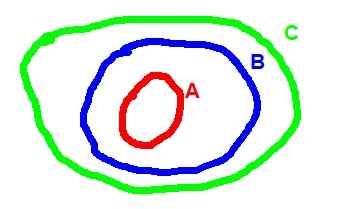figur 2. (A ⊂ B) ^ (B ⊂ C) => A ⊂ C

- Operationer mellan uppsättningarna

Genomskärning

Korsningen är en operation mellan två uppsättningar som resulterar i en ny uppsättning som tillhör samma universella uppsättning av de två första. I den meningen är det en stängd operation.

Symboliskt formuleras korsningens operation enligt följande:

A⋂b = x / x∈A ^ x∈B

Ett exempel är som följer: Ställ in ett av bokstäverna i ordet "element" och ställ in B i bokstäverna i ordet "upprepade", är skärningspunkten mellan A och B skriven så här:

A⋂b = e, l, m, n, t, s ⋂ r, e, p, t, i, d, o, s = e, t, s . Den universella uppsättningen A, från B och även A⋂B är uppsättningen av bokstäverna i det spanska alfabetet.

Union

Föreningen mellan två uppsättningar är den uppsättning som bildas av de element som är gemensamma för de två uppsättningarna och de icke -vanliga elementen i de två uppsättningarna. Unionens operation mellan uppsättningarna uttrycks symboliskt på följande sätt:

A∪b = x/x∈A v x∈B

Skillnad

Driften av uppsättningen åtminstone uppsättningen betecknas av A-B. A-B är en ny uppsättning som bildas av alla element som finns i A och som inte tillhör B. Symbolen är skriven så här:

A - b = x/ x ∈ A ^ x ∉ b

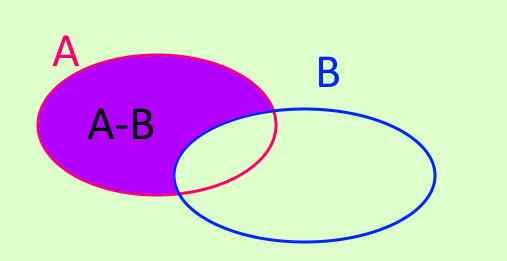Figur 3. A - b = x/ x ∈ A ^ x ∉ b

Symmetrisk skillnad

Den symmetriska skillnaden är en operation mellan två uppsättningar där den resulterande uppsättningen består av elementen som inte är gemensamma för de två uppsättningarna. Den symmetriska skillnaden symboliskt representeras enligt följande:

A⊕b = x/ x∈ (a-b) ^ x∈ (b-a)

Exempel

Exempel 1

Venn -diagrammet är ett grafiskt sätt att representera uppsättningarna. Exempelvis representeras C av bokstäverna i orduppsättningen enligt följande:

Exempel 2

Det visas nedan genom Venn -diagram att uppsättningen vokaler i ordet "set", är en delmängd av uppsättningen av bokstäverna i ordet "uppsättning".

Kan tjäna dig: kvotprovtagning: metod, fördelar, nackdelar, exempel

Exempel 3

Uppsättning Ñ Från bokstäverna i det spanska alfabetet är det en ändlig uppsättning, denna uppsättning i förlängningen skrivs så här:

Ñ = A, B, C, D, E, F, G, H, I, J, K, L, M, N, ñ, O, P, Q, R, S, T, U, V, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, X, Y, Z och dess Kardinalitet är 27.

Exempel 4

Uppsättning V Från vokalerna på spanska är det en delmängd av ñ -uppsättningen:

V ⊂ Ñ Därför är det en ändlig uppsättning.

Den ändliga uppsättningen V Utökat sätt det är skrivet så här: V = A, E, I, O, U och dess kardinalitet är 5.

Exempel 5

Med tanke på uppsättningarna A = 2, 4, 6, 8 och B = 1, 2, 4, 7, 9 Bestäm a-b och b-a. 

A - B är de element som de inte är i B:

A - B = 6, 8

B - A är elementen i B som inte finns i A:

B - A = 1, 7, 9

Löst övningar

Övning 1

Skriv symboliskt och även i förlängningen Kronbladet av naturliga siffror ännu lägre än 10.

Lösning: P = x∈ N / x < 10 ^ x mod 2 = 0

P = 2, 4, 6, 8

Övning 2

Antag hela till det som bildas av de naturliga siffrorna som är faktorer på 210, och uppsättningen B som bildas av de naturliga kusinerna lägre än 9. Bestäm båda uppsättningarna i förlängningen och fastställa vilken relation det finns mellan de två uppsättningarna.

Lösning: För att bestämma elementen i uppsättning A måste du börja med att hitta faktorerna i det naturliga nummer 210:

210 = 2 * 3 * 5 * 7

Set A är skriven:

A = 2, 3, 5, 7

Vi fortsätter att överväga Set B, som är kusinerna mindre än 9. 1 är inte kusin eftersom den inte uppfyller definitionen av kusin: "Ett nummer är kusin om och bara om den har exakt två delare 1 och själva numret". De 2 är jämnt och samtidigt är kusin eftersom den uppfyller definitionen av kusin, de andra kusinerna mindre än 9 är 3, 5 och 7. Så den uppsättningen B är:

B = 2, 3, 5, 7

Därför är de två uppsättningarna desamma: a = B.

Övning 3

Bestäm den uppsättning vars element x skiljer sig från x.

Lösning: C = x / x ≠ x

Som alla element, antal eller objekt är lika med sig själv, kan set C inte vara annat än den tomma uppsättningen:

C = Ø

Övning 4

Vara uppsättningen av n av naturliga siffror och z uppsättningen av hela siffror. Bestämma n ⋂ z y n ∪ z.

Lösning: 

N ⋂ z = x ∈ Z / x ≤ 0 = (-∞, 0]

N ∪ z = z eftersom n ⊂ z.

Referenser

1. Garo, m. (2014). Matematik: Kvadratiska ekvationer: Hur löser en kvadratisk ekvation. Marilù garo.
2. Haeussler, E. F., & Paul, r. S. (2003). Matematik för administration och ekonomi. Pearson Education.
3. Jiménez, J., Rodríguez, m., Estrada, r. (2005). Matematik 1 september. Tröskel.
4. Dyrbar, c. T. (2005). Matematikkurs 3o. Redaktionell progreso.
5. Matematik 10 (2018). "Exempel på ändliga uppsättningar". Hämtad från: Matematik10.netto
6. Wikipedia. Inställningsteori. Återhämtad från: är.Wikipedia.com