Molekylär orbital teori

Vad är molekylär orbital teori?

De Molekylär orbital teori (Tom) Det är en matematisk modell som utvecklats för att förklara de fysikalisk -kemiska egenskaperna hos molekyler, såsom absorption och utsläpp av strålning, elektrisk konduktivitet, liksom den elektroniska naturen hos dess länkar. Detta anser, till skillnad från Valencia Link Theory (TEV), att elektroner flyttas i hela molekylen, utan att vara sannolikt beläget i länkarna.

Därför tillämpar den molekylära orbitalteorin samma kvantprinciper som dikterar vågfunktionerna för atomorbitaler och därmed beskriver energitillståndet för elektroner i atomer; Först nu, adresserar de så kallade molekylära orbitalerna, härstammar från de linjära kombinationerna av atomorbitalerna i atomerna som är kopplade.

Paramagnetismen av flytande syre, och därför dess attraktion för magneter, förklaras tack vare molekylära orbitalteorin. Källa: Pieter Kuipeper via Wikipedia.

Den molekylära orbitalteorin fungerar då och arbetar med molekylära orbitaler, deras elektroniska och rumsliga fördelningar, liksom diagrammen över deras respektive energier, som tillåter observera energiklyftan som skiljer dem. Förklara framför allt paramagnetismen för vissa ämnen, såsom molekylärt syre i flytande tillstånd (se ovan).

O₂, Beskrivs av Lewis strukturer och Valencias länkteori, har den alla sina parade elektroner, så i teorin borde det vara diamagnetiskt. I praktiken har det emellertid visats att det faktiskt är paramagnetiskt, det vill säga att det saknas elektroner; specifikt ett par saknade elektroner.

Från konstruktionen av OM -diagrammet (molekylära orbitaler) för O₂, En homonukleär diatomisk molekyl, kan man se att det i själva verket kommer att finnas två högenergi som saknas elektroner. Inte bara detta, utan snurret och positionen för dessa elektroner i OMS förklarar också andra elektroniska tillstånd i OR₂ (enda).

Andra av de viktigaste triumferna i molekylär orbital teori är att det hjälper till att förutsäga den möjliga förekomsten av diatomiska molekyler, liksom deras relativa stabilitet. Således är molekylär orbital teori rätt i förutsägelsen av molekyler såsom B₂ och li₂, Även när de bara kan upptäcka i ångfasen vid höga temperaturer. Dessutom avvisar denna teori förekomsten av det hypotetiska jag har₂ eller ne₂.

Typer av molekylära bindningar och orbitaler

Liksom med Valencia Link Theory, i den molekylära orbitalteorin, beaktas flera typer av länkar beroende på riktningen för överlappningen av atomorbitaler som deltar i den kemiska bindningen. Bland de viktigaste och närvarande i molekylär natur har vi sigma- och PI -bindningarna.

Sigma

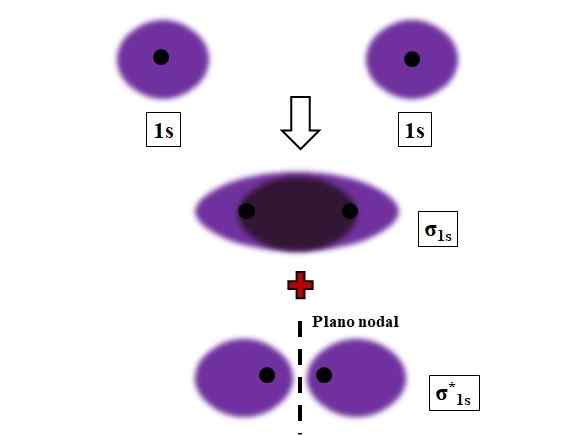Bildning av σ1s och σ1s* länkar under överlappningen av två atomiska orbitaler 1s. Källa: Gabriel Bolívar.

Sigma, σ -bindningar är etablerade när atomiska orbitaler överlappar varandra, i förhållande till en imaginär internukleär axel som förbinder de två kärnorna som närmar sig.

Tänk till exempel på σ -länken som bildas när två 1S -atomiska orbitaler, enligt en väteatom, är nära mycket kort avstånd (bild ovan). Eftersom 1S -orbitaler är symmetriska kommer deras överlappning alltid att vara frontal; Därför kommer de alltid att generera molekylära orbitaler σ_1s och σ_1s*.

Notera nu att molekylär orbital σ_1s visar en elektronisk densitet koncentrerad i utrymmet som skiljer de två kärnorna. Detta innebär att i en orbital σ_1s Sannolikheten för att hitta en elektron är maximal i detta område i molekylen. Elektronerna i σ_1s De flyttas i hela utrymmet som täcker den lila färgen.

Å andra sidan, i omloppet σ_1s* Vi har ett nodalplan mellan de två kärnorna. Detta innebär att sannolikheten för att hitta en elektron mellan det utrymmet är lika med noll. Observera att i orbital σ_1s* Elektroner beskriver positioner runt var och en av de två kärnorna; inte runt molekylen som helhet.

Kan tjäna dig: radio: struktur, egenskaper, användningar, erhålla

Pi

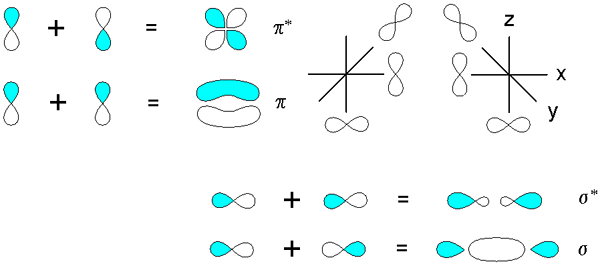Sigma- och PI -bindningar härrörande från överlappningen av orbitaler p. Källa: V8Rik på In.Wikipedia, CC BY-SA 3.0, via Wikimedia Commons

Tänk nu på molekylära bindningar och orbitaler. Dessa inträffar när överlappningen av orbitalerna inträffar i en riktning vinkelrätt mot den internukleära axeln, som är godtyckligt fixerad i någon av axlarna på det kartesiska planet. Förutsatt att vi pratar om en 2p orbital_x, 2p orbital_och Det är gratis att upprätta en PI -länk (se blå och vita lober).

När två orbitaler 2p_och Två molekylära orbitaler har sitt ursprung: π_2py och π_2py*; Den första har den högsta elektroniska densiteten och under den internukleära axeln, medan den andra liknar en fyra -matt blomma, där sannolikheten för att hitta elektroner är mycket lägre.

Å andra sidan, orbitalerna 2p, för att säga 2p_x, De kan också överlappa varandra för att komma från en σ -bindning och två molekylära orbitaler σ_2px och σ_2px*. Som i fallet σ_1s och σ_1s*, The Orbital σ_2px visar större elektronisk densitet mellan de två kärnorna; vilket strider mot σ_2px*, där elektroner är orienterade mot sidorna på utsidan.

Länk

Lindande molekylära orbitaler är de som bidrar till molekylens stabilitet. Det vill säga, de måste ha mindre energi jämfört med atomiska orbitalerna hos enskilda atomer innan de länkar och bildar molekylen. I dessa orbitaler flyttas elektronerna av alla molekylens dimensioner som helhet.

I OM -diagrammen kommer dessa alltid att ligga under atomorbitalerna som kombineras för att bilda dem. Detta kommer att ses mer i detalj i nästa avsnitt.

Anti -hut

De anti -housing molekylära orbitalerna är å andra sidan de som destabiliserar molekylen. De symboliseras med en asterisk (*), och deras energier är högre än för atomorbitalerna som har sitt ursprung dem. I dessa orbitaler flyttas elektronerna ganska oregelbundet, som om molekylen var elektroniskt fragmenterad.

I OM -diagram kommer de alltid att vara belägna ovanför de atomiska orbitalerna som kombineras för att bilda dem.

Inte kopplad

Samtidigt är icke -kopplingsbanor, såväl som deras elektroner, de som inte bidrar eller skadar molekylens stabilitet. Hans energier är mycket lik de hos atomiska orbitaler.

Länkordning

Länkordningen blir i den molekylära orbitalteorin, liksom länknumret finns i Valencia -länkteorin: ett mått på länken i en molekyl. Således motsvarar en länkorder lika med 1 en enkel länk (-). Och en länkorder (eller.e) lika med 2, motsvarar en dubbelbindning (=). Så vidare.

Denna ordning bestäms från räkningen av elektroner i OM -diagrammen för en viss molekyl. För att göra detta måste följande formel tillämpas:

antingen.E = (antal länkade elektroner - Antal anti -hutelektroner)/2

Länkelektroner bidrar till molekylen för att stabilisera, medan anti -fiende elektroner destabiliserar den. Därför, ju mer anti -Sung -elektroner, desto mindre eller.E, och molekylen tenderar att vara mycket instabil. När O.E är lika med 0, det betyder att molekylen inte finns (eller åtminstone i teorin).

OM -diagram

I OM -diagrammen representeras energierna från molekylära orbitaler, och dess elektroniska fyllning visualiseras också, vilket följer reglerna för Aufbauf och Sinn, liksom principen om uteslutning av Pauling. Tänk till exempel på följande två diagram:

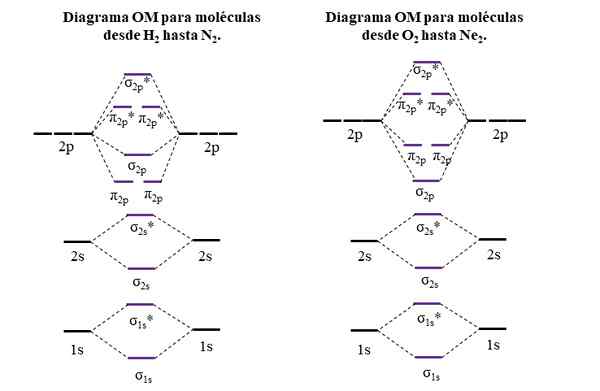OM -diagram för molekyler från den första och andra perioden av den periodiska tabellen. Källa: Gabriel Bolívar.

Horisontella linjer på sidorna, svarta, representerar atomiska orbitalernas energi. Istället är centrala horisontella linjer, lila, energierna i molekylära orbitaler. Observera hur länk och anti -agent OM: er distribueras (*) i förhållande till atomiska orbitaler hos enskilda atomer.

Det kan tjäna dig: en aminogrupp (NH2): Struktur, egenskaper, exempel

Observera också att i det högra diagrammet, om σ_{2 p} De byter plats med π_{2 p}. Detta inträffar med molekylerna av O₂, F₂, och den hypotetiska NE₂.

Exempel

I följande exempel kommer OM att fortsätta med elektronerna, beräkna länkordningen och göra förutsägelser om bindningens kraft eller stabilitet i den aktuella molekylen.

H₂

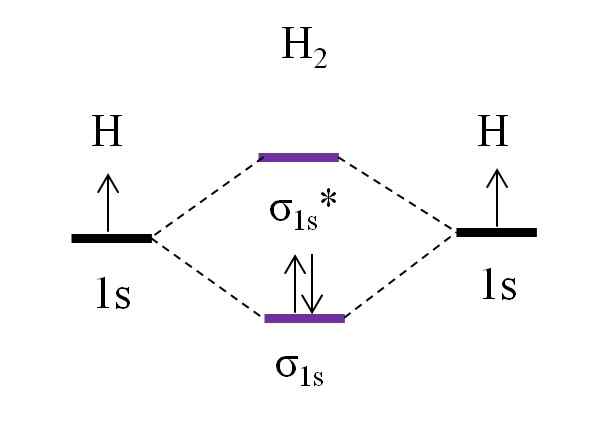OM -diagram för dihydrogenmolekyl. Källa: Gabriel Bolívar.

Börjar med den enklaste molekylen, den för dihydrogen, h₂, Två H -atomer är kopplade genom att kombinera sina två 1s atomiska orbitaler för att bilda två molekylära orbitaler σ_1s och σ_1s*. De två elektronerna fortsätter sedan med att fylla molekylära orbitaler.

Först är orbitalet σ fylld_1s, Eftersom det är den minsta energin (Aufbauf -regeln). Sedan måste den andra elektronen avsluta fylla orbitalet σ_1s Innan du klättrar i omloppet σ_1s* (Sänkregel). Och slutligen leder denna andra elektron sin snurr i motsatt riktning till den första elektronen (Pauling Excrising Principle). Således är de två elektronerna belägna i den länkade orbitalen σ_1s.

Vad sägs om länkordern? I länken Molecular Orbital σ_1s Vi har två elektroner; Medan i anti -HELL Molecular Orbital σ_1s* vi har inga. Därför skulle beräkningen vara:

antingen.E = (2-0)/2

= 1

Varelse eller.Och lika med 1 betyder det att länken som förenar de två väteatomerna är enkel: H-H. I allmänhet, om detta värde är lika med eller större än 1, sägs det att molekylen finns och är stabilt.

han₂

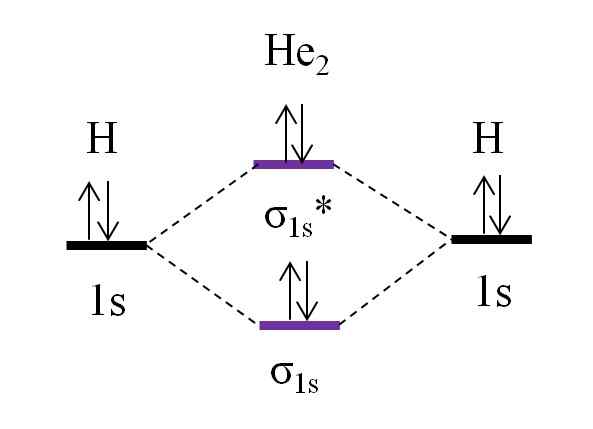OM -diagram för hypotetisk diheliomolekyl. Källa: Gabriel Bolívar.

Anta nu att du har molekylen i han₂. Ovan ser vi att dess omdiagram är mycket lik H₂, Med ytterligare 2 elektroner som finns i orbital σ_1s*. När det finns totalt 4 elektroner som lägger till de två atomerna, måste det också finnas 4 elektroner i alla de resulterande molekylära orbitalerna.

Bestämmer O.E för jag han₂ vi kommer att ha:

antingen.E = (2-2)/2

= 0

Detta innebär att det inte finns någon möjlig länk som de två heliumatomerna. I själva verket har förekomsten av denna molekyl inte identifierats, vilket överensstämmer med förutsägelserna om molekylär orbitalteori.

B₂

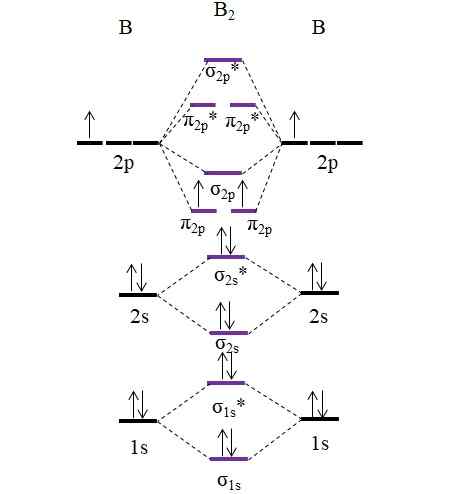OM -diagram för B2 -molekylen. Källa: Gabriel Bolívar.

Observera att vid bildandet av molekylära orbitaler beaktas också elektronerna i de inre skikten; Inte bara de i Valencia.

Således, i exemplet med diboromolekylen, b₂, Varje boratom bidrar totalt 5 elektroner, varav 3 är från Valencia; Dessa är de av deras 2s och 2p orbitaler. De två elektronerna i orbitalerna 2p är placerade i olika molekylära orbitaler π_{2 p} Med parallella ryggar (sjunkningsregel).

Vi fortsätter sedan att beräkna länkordningen:

antingen.E = (6-4)/2

= 1

Därför förväntas molekylen ha en enkel B-B-länk. B₂ Det är en molekyl som bara finns i ångstadiet vid mycket höga temperaturer, eftersom bor under normala förhållanden antar mer komplexa nätverksstrukturer och mönster.

C₂ och C₂^2-

Tänk först på OM -diagrammet för molekyl c₂:

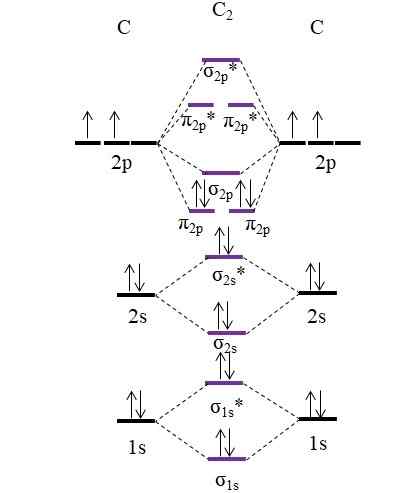OM -diagram för molekyl C2. Källa: Gabriel Bolívar.

Nu placeras de två nya elektronerna som tillhandahålls av kolatomer igen i molekylära orbitaler π_{2 p} Men med motsatta snurr (Pauling Excrising Principle).

Bestämma din länkorder vi kommer att ha:

antingen.E = (8-4)/2

= 2

Observera att molekylära orbitaler π_{2 p} Lägg till 4 elektroner som binder till formeln. Att vara denna ordning lika med 2, det betyder att molekyl C₂ Den har en dubbelbindning, c = c. Återigen, molekyl C₂, Även kallad diatomiskt kol, det finns bara ångfas vid höga temperaturer, och det är en av de enklaste allotropiska kolformerna.

Och hur är det med C₂^2-? Ditt OM -diagram är som följer:

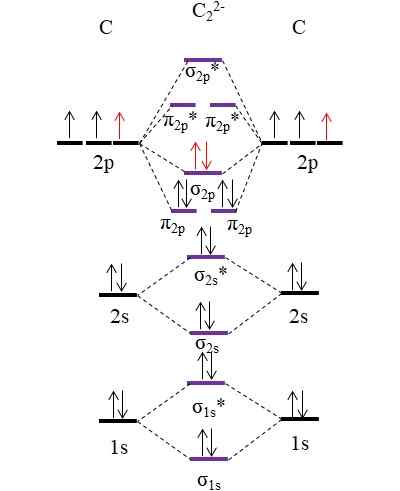OM -diagram för anjon C22-. Källa: Gabriel Bolívar.

De två nya elektronerna (röda pilar) är placerade i den länkande molekylära orbitalet σ_{2 p}. Detta antar alltså att varje kolatom bidrar med en av de två negativa laddningarna (för ett oxidationstillstånd på -1).

Kan tjäna dig: Mercury Fulminate: Struktur, egenskaper, erhållning, användning

Beräkna din länkorder vi kommer att ha:

antingen.E = (10-4)/2

= 3

Det vill säga anjon c₂^2-, Även kallad anjon acetyluro, den har en trippellänk, [C≡C]^2-. Det är en relativt stabil anjon med en stor länkkraft; Beroende på dess motsvarighetsjoner kan det emellertid komma från explosiva föreningar.

N₂ och n₂⁺

Den berömda kvävemolekylen, n₂, Det kan också beskrivas perfekt genom att använda molekylära orbitaldiagram:

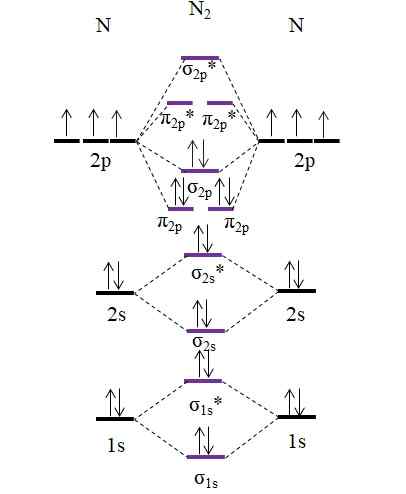OM -diagram för N2 -molekylen. Källa: Gabriel Bolívar.

Observera att detta diagram är exakt samma som för anjon c₂^2-. Detta betyder att n₂ och C₂^2- De är isolektroniska. Sådant faktum innebär dock inte att båda arter uppför sig på samma sätt. N₂, neutral, är mycket mer stabil än C₂^2-, negativ, även om båda har en länkorder lika med 3, N≡N.

Och hur är det med katjon n₂⁺? Låt oss titta på ditt OM -diagram:

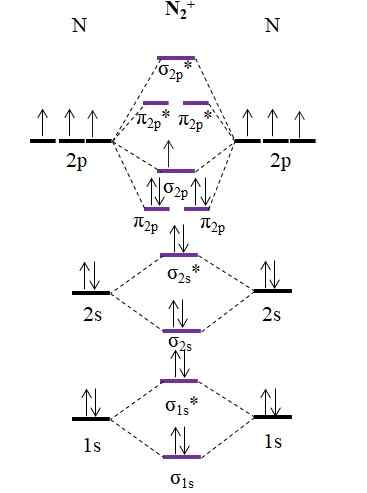OM -diagram för katjon N2+. Källa: Gabriel Bolívar.

Som katjon n₂⁺ Den har en mindre elektron, detta tas bort den molekylära orbitalet σ_{2 p}. N₂ Det är diamagnetiskt, medan n₂⁺ Det är paramagnetiskt. Och hans länkorder är:

antingen.E = (9-4)/2

= 2.5

En 2 2 -länk.5 skulle representeras med två rader och en poäng. En sådan sak är emellertid inte mycket meningsfull i Valencias teori eller i Lewis strukturer. Eftersom den här länkordningen är mindre än 3, styrkan för länken som finns i n₂⁺ är lägre än n₂, Så det är mer instabilt.

ANTINGEN₂, ANTINGEN₂^2- Jag₂²⁺

Låt oss nu se en annan mycket viktig molekyl för livet: molekylärt eller diatomiskt syre, eller₂. Enligt Valencias teori och Lewis strukturer bör den vara diamagnetisk; Men experimentellt har det visat sig vara paramagnetiskt, så det har försvunnit elektroner någonstans.

Nedan jämför vi OM -diagrammen för O₂ och joner eller₂^2- (oxid) och O₂²⁺ (Oxidering):

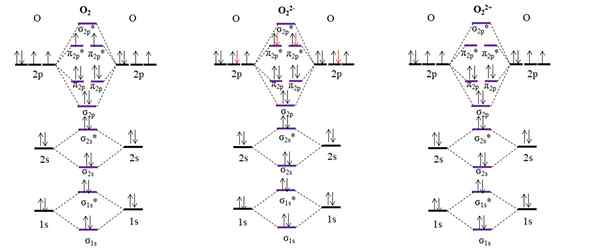OM -diagram för molekylärt syre och två av dess huvudjoner. Källa: Gabriel Bolívar.

OM -diagrammet för O₂ Prov, till skillnad från de tidigare, att de molekylära orbitalerna σ_{2 p} och π_{2 p} Ändra sin energiposition. Vi ser också effektivt att det finns två saknade elektroner i orbitalerna π_{2 p}*, som förklarar den paramagnetiska karaktären av syre (nämns i början av artikeln).

Å andra sidan har vi också OM -diagrammet för anjon eller₂^2-, Oändligt sprids i kosmos (månar, planeter, kometer, asteroider, etc.). Den har två extra elektroner (röda pilar), som slutar på att fylla π -orbitalerna_{2 p}*, parar alla elektroner. Följaktligen eller₂^2- Det är diamagnetiskt.

Vi överväger också OM -diagrammet för oxidering eller₂²⁺. Den har två elektroner mindre än O₂, lämnar tomma orbitalerna π_{2 p}*. Alla dess elektroner är parade, och därför är den diamagnetisk.

Länkorder för o₂, ANTINGEN₂^2- Jag₂²⁺ De är respektive: 2 (o = o), 1 [o-o]^2- och 3 [o≡o]²⁺. Därför o₂²⁺ skulle ha den starkaste länken.

Fördelar och nackdelar

Fördelar

Bland fördelarna med molekylär orbital teori kan vi citera följande:

-Det gör det möjligt att utvärdera länkorder som vanliga inte skulle vara mycket meningsfulla i Valencia Link Theory

-Det korrelerar bra med diamagnetism och paramagnetism av molekyler

-Avståndet som separerar molekylära orbitaler i diagrammen är lika med ΔE och tjänar till att förklara elektroniska övergångar produkt av fotonabsorption

-Tillämpar inte bara för homonukleära diatomiska molekyler, utan också för heteronukleära molekyler, såsom Co₂ och bensen

-Den utvidgar sin modell mot andra typer av föreningar, såsom oorganiska komplex, så den stöder teorin om ligandens fält

-Hänsyn till att elektroner flyttas i hela molekylen är bekvämt att förklara många av de fysikalisk -kemiska egenskaperna

Nackdelar

Och bland några av nackdelarna med molekylär orbitalteori har vi, till slut:

-Det är mycket abstrakt och kräver en djup matematisk förståelse för att fullt ut förstå det

-Molekulationsdiagram som CO₂, Co, h₂Eller och andra kan de vara för tråkiga för att utarbeta och förklara

-Han säger ingenting om specifika regioner eller länkar till en stor molekyl

-Det ger inte heller någon information om molekylgeometri (trigonal plan, fyrkantigt plan, tetraedral, etc.).

-Det är inte så grafiskt som Valencias länkteori

Molekylära orbitalteorin är i slutsatsen en teori som kompletterar teorin om Valencia -länken för att ha ett bredare och mer fullständigt panorama över molekylspektrumet.

Referenser

1. Whitten, Davis, Peck & Stanley. (2008). Kemi. (8: e upplagan.). Cengage Learning.
2. Shiver & Atkins. (2008). Oorganisk kemi. (Fjärde upplagan). MC Graw Hill.
3. Wikipedia. (2020). Orbital molekylär teori. Hämtad från: i.Wikipedia.org
4. Stephen Lower. (7 september 2020). Orbital molekylär teori. Kemi librettexts. Återhämtad från: kem.Librettexts.org
5. Steven a. Botekar. (2017). Orbital molekylär teori. Hämtad från: Chemed.Kem.Purdu.Edu
6. Pressböcker. (s.F.). Kapitel 8: Orbital molekylär teori. Hämtad från: OpenTextbc.Växelström