Bolzano -teorem

Vi förklarar vad Bolzanos teorem är, dess tillämpningar och sätter lösade övningar

Vad är Bolzanos teorem?

han Bolzano -teorem Den konstaterar att om en funktion är kontinuerlig vid alla punkter i ett stängt intervall [A, B] och det uppfylls att bilden av "A" och "B" (under funktionen) har motsatta tecken, kommer det åtminstone att finnas En punkt "C" i det öppna intervallet (A, B), så att funktionen utvärderas i "C" kommer att vara lika med 0.

Denna sats anges av filosofen, teologen och matematikern Bernard Bolzano 1850. Denna forskare, född i den nuvarande Tjeckien, var en av de första matematikerna i historien som gjorde en formell demonstration av egenskaperna hos kontinuerliga funktioner.

Satsförklaring

Bolzanos teorem är också känt som teoremet för mellanvärden, vilket hjälper till att bestämma specifika värden, särskilt nollor, av vissa verkliga funktioner hos en verklig variabel.

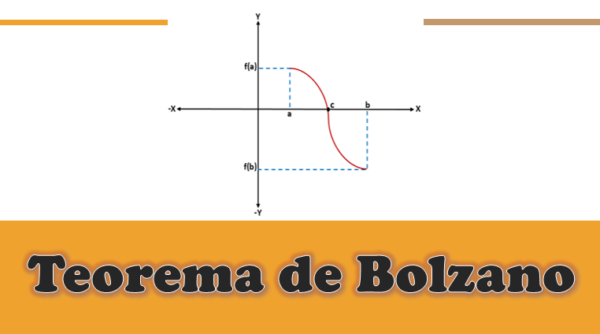
I en given funktion fortsätter f (x) -det vill säga att f (a) och f (b) är anslutna med en kurva-, där f (a) är under x -axeln (är negativ) och f (b) Med ovanför X -axeln (den är positiv), eller vice versa, kommer det att finnas en skärpunkt på x -axeln som kommer att representera ett mellanvärde "C", som kommer att vara mellan "A" och "B", och värdet av f (c) det kommer att vara lika med 0.

När du grafiskt analyserar Bolzanos teorem kan det vara känt att för alla kontinuerliga F -funktioner definierade i ett intervall [a, b], där f (a)_*f (b) är mindre än 0, det kommer att finnas minst en rot "c" av den funktionen inom intervallet (a, b).

Denna sats fastställer inte antalet punkter som finns i det öppna intervallet, det säger bara att det finns minst 1 poäng.

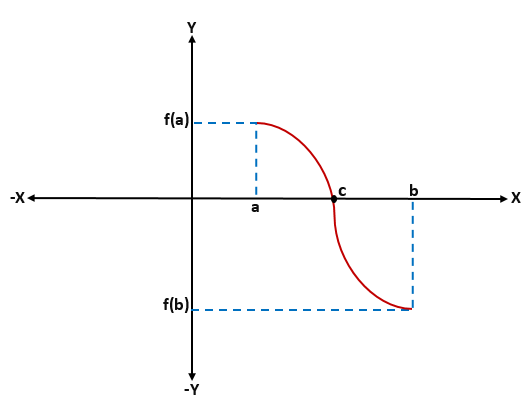
Demonstration av bolzano -teorem

För att demonstrera Bolzanos teorem antas det utan förlust av allmänhet att f (a) 0; På detta sätt kan det finnas många värden mellan "a" och "b" för vilka f (x) = 0, men det är bara nödvändigt att visa att det finns en.

Kan tjäna dig: imaginära nummer: egenskaper, applikationer, exempel

Det börjar utvärdera F vid mittpunkten (A+B)/2. Om f ((a+b)/2) = 0 så slutar testet här; Annars är f ((a+b)/2) positiv eller negativ.

En av halvorna av intervallet [a, b] väljs, så att tecknen på funktionen utvärderas i ändarna är olika. Detta nya intervall kommer att vara [A1, B1].

Nu, om F utvärderas vid mittpunkten för [A1, B1] inte är noll, utförs samma operation före; Det vill säga, hälften av detta intervall som uppfyller skyltens tillstånd väljs. Vara detta nya intervall [A2, B2].

Om denna process fortsätter kommer det att finnas två successioner an och bn, så att:

en växer och bn minskar:

A ≤ a1 ≤ a2 ≤ ... ≤ a ≤ .. . ≤ .. . ≤ Bn ≤ .. . ≤ B2 ≤ B1 ≤ B.

Om längden på varje intervall [AI, BI] beräknas måste du:

B1-A1 = (B-A)/2.

B2-A2 = (B-A)/2².

.. .

bn-an = (b-a)/2^n.

Därför är gränsen när N tenderar att oändligheten (Bn-AN) är lika med 0.

Att använda det en växer och begränsas och bn minskar och begränsas finns det ett värde "c" så att:

A ≤ a1 ≤ a2 ≤ ... ≤ a ≤ .. .≤ C ≤ .. . ≤ Bn ≤ .. . ≤ B2 ≤ B1 ≤ B.

LIM -gränsen är "C" och gränsen för Bn är också "C". Därför, med tanke på alla Δ> 0, finns det alltid en "n" så att intervallet [an, bn] finns i intervallet (c-Δ, c+Δ).

Nu måste det visas att f (c) = 0.

Om f (c)> 0, eftersom f är kontinuerligt, finns det en ε> 0 så att f är positiv under hela intervallet (c -ε, c+ε). Som nämnts ovan finns det emellertid ett "n" -värde så att f ändras inloggning [an, bn] och dessutom [an, bn] finns i (c -ε, c+ε), vad är vad som är en motsägelse.

Om f (c) 0 så att f är negativt under hela intervallet (c -ε, c+ε); Men det finns ett "n" -värde som f ändrar inloggning [an, bn]. Det visar sig att [an, bn] finns inom (c -ε, c+ε), vilket också är en motsägelse.

Kan tjäna dig: tecken på gruppering

Därför f (c) = 0 och det här var det som ville demonstreras.

Vad är bolzano -teoremet för?

Från sin grafiska tolkning används Bolzanos teorem för att hitta rötter eller nollor i en kontinuerlig funktion, genom bisension (tillvägagångssätt), som är en inkrementell sökmetod som alltid delar intervallen i 2.

Således, om funktionen ändras under ett intervall utvärderas F -funktionen vid mittpunkten, som uttrycks enligt följande: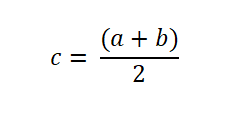Roten hittas när f (c) = 0. Om inte, analyseras tecknet på f (c) för att avgöra om det motsätter sig tecknet på f (a) eller det för f (b).

Sedan tas ett intervall [a, c] eller [c, b] där skyltändringen inträffar, och processen upprepas tills intervallet är mindre och mindre för att närma dig det värde du vill ha; det vill säga till värdet som funktionen gör 0.

Sammanfattningsvis, för att tillämpa bolzano -teoremet och därmed hitta rötter, begränsa nollorna på en funktion eller ge en lösning på en ekvation, utförs följande steg:

1. Det verifieras om F är en kontinuerlig funktion i intervallet [A, B].
2. Om intervallet inte ges måste man hitta en där funktionen är kontinuerlig.
3. Det verifieras om intervallets ändar ger motsatta tecken när de utvärderas i f.
4. Om motsatta tecken inte erhålls måste intervallet delas upp i två underintervaller med mittpunkten.
5. Utvärdera funktionen vid mittpunkten och verifiera att bolzano -hypotesen är uppfylld, där f (a) _* f (b) < 0.
6. Beroende på tecknet (positivt eller negativt) av det hittade värdet upprepas processen med en ny underinterval tills den nämnda hypotesen uppfylls.

Kan tjäna dig: Icke -linjär programmering: Metoder och övningar

Löst övningar

Övning 1

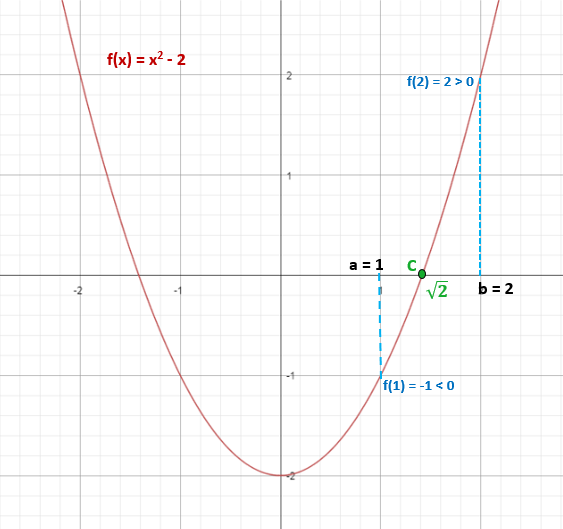
Bestämma om funktionen f (x) = x² - 2, har minst en verklig lösning i intervallet [1,2].

Lösning

Du har funktionen f (x) = x² - 2. Som är polynom betyder det att det är kontinuerligt i alla intervall.

Det uppmanas att avgöra om den har en verklig lösning i intervallet [1, 2], så nu behöver du bara ersätta ändarna på intervallet i funktionen för att veta tecknet på dessa och vet om de uppfyller villkoret att vara annorlunda:

f (x) = x² - 2

f (1) = 1² - 2 = -1 (negativ)

f (2) = 2² - 2 = 2 (positiv)

Därför, tecken på F (1) ≠ tecken F (2).

Detta säkerställer att det finns minst en punkt "C" som tillhör intervallet [1,2], där f (c) = 0.

I detta fall kan "C" -värdet enkelt beräknas enligt följande:

x² - 2 = 0

x = ± √2.

Således tillhör √2 ≈ 1,4 intervallet [1,2] och uppfyller att f (√2) = 0.

Övning 2

Visa att ekvation x⁵ + x + 1 = 0 har minst en riktig lösning.

Lösning

Först noterar vi att f (x) = x⁵ + X + 1 är en polynomfunktion, vilket innebär att den är kontinuerlig i alla verkliga siffror.

I det här fallet ges inget intervall, så du måste välja värden intuitivt, helst nära 0, för att utvärdera funktionen och hitta teckenändringarna:

Om intervallet [0, 1] används måste det:

f (x) = x⁵ + x + 1.

f (0) = 0⁵ + 0 + 1 = 1> 0.

f (1) = 1⁵ + 1 + 1 = 3> 0.

Eftersom det inte finns någon teckenförändring upprepas processen med ytterligare ett intervall.

Om intervallet [-1, 0] används måste du:

f (x) = x⁵ + x + 1.

f (-1) = (-1)⁵ + (-1) + 1 = -1 < 0.

f (0) = 0⁵ + 0 + 1 = 1> 0.

I detta intervall finns en teckenändring: tecken på f (-1) ≠ tecken på f (0), vilket innebär att funktionen f (x) = x⁵ + X + 1 har minst en riktig rot "c" i intervallet [-1, 0], så att f (c) = 0. Med andra ord är det sant att x⁵ + x + 1 = 0 har en verklig lösning i intervallet [-1,0].