Lamys teorem

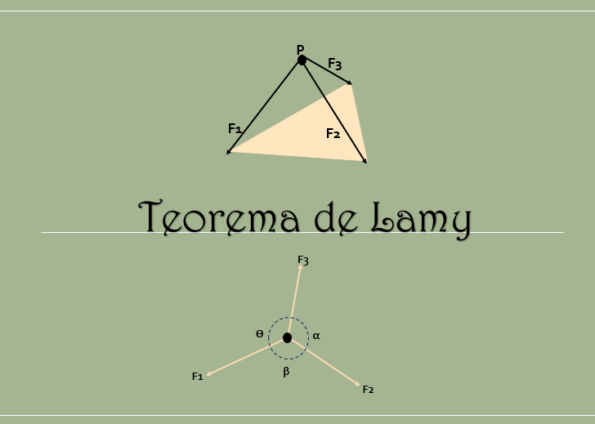
Lamys sats konstaterar att när en styv kropp är i balans och på handlingen av tre kopplingskrafter (krafter som är i samma plan), överensstämmer deras handlingslinjer vid samma punkt.

Satsen härleddes av den franska fysikern och religiös. Det används allmänt för att hitta värdet på en vinkel, en kraftverk eller för att bilda krafternas triangel.

Förklaring

Satsen konstaterar att för att villkoren för balans ska uppfyllas måste krafterna vara coplanares; det vill säga, summan av de krafter som utövas på en punkt är noll.

Som framgår av följande bild uppfylls det dessutom att genom att förlänga handlingslinjerna för dessa tre krafter, instämmer de vid samma punkt.

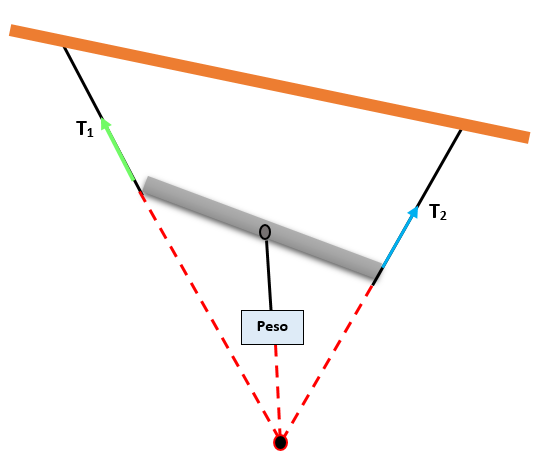
Således, om tre krafter som är i samma plan och samtidiga, kommer storleken på varje kraft att vara proportionell mot skötet i motsatt vinkel, som bildas av de andra två krafterna.

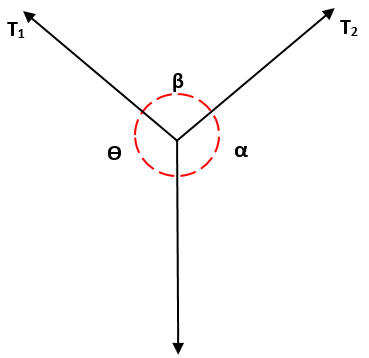
Detta måste T1, från bröstet av a, det är lika med förhållandet T2 / ß, vilket i sin tur är lika med förhållandet mellan T3 / ɵ, det vill säga:

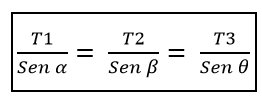
Därifrån följer det att modulerna för dessa tre krafter måste vara desamma om vinklarna som bildar varje kraftpar är lika med 120º.

Det finns möjligheten att en av vinklarna är stöt (mått mellan 90⁰ och 180⁰). I så fall kommer bröstet i den vinkeln att vara lika med bröstet i den kompletterande vinkeln (i dess par mäter det 180⁰).

Träning löst

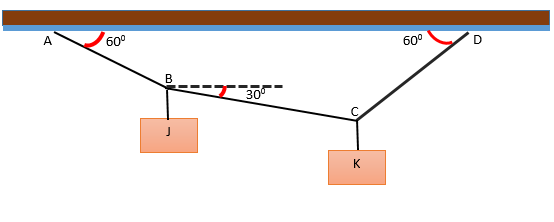
Det finns ett system bildat av två J- och K -block, som hänger på flera strängar som bildar vinklar med avseende på horisontellt, som visas i figuren. Systemet är i jämvikt och J -blocket väger 240 n. Bestäm vikten på block K.

Lösning

Genom principen om handling och reaktion kommer spänningarna som utövas i block 1 och 2 att vara lika med vikten av dessa.

Nu är ett gratis kroppsdiagram byggt för varje block och bestämmer därmed vinklarna som bildar systemet.

Det är känt att repet som går till A till B, har en vinkel på 30⁰ , så att vinkeln som kompletterar den är lika med 60⁰ . På så sätt når du 90⁰.

Å andra sidan, där punkt A ligger, finns det en vinkel på 60⁰ med avseende på horisontellt; Vinkeln mellan vertikal och t_TILL Det kommer att vara = 180⁰ - 60⁰ - 90⁰ = 30⁰.

Således erhålls det att vinkeln mellan AB och BC = (30⁰ + 90⁰ + 30⁰) och (60⁰ + 90⁰ + 60) = 150⁰ och 210⁰. När du går med verifieras det att den totala vinkeln är 360⁰.

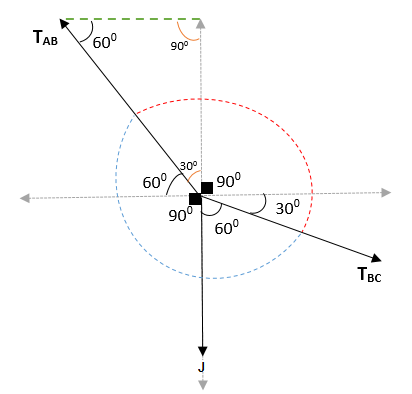
Tillämpa Lamys teorem du måste:

T_{före Kristus}/ sin 150⁰ = P_TILL/ sin 150⁰

T_{före Kristus} = P_TILL

T_{före Kristus} = 240n.

Vid punkt C, var är blocket, vinkeln mellan horisontellt och BC -repet är 30 är 30 är 30⁰, Så den komplementära vinkeln är lika med 60⁰.

Å andra sidan finns det en vinkel på 60⁰ vid CD -punkten; Vinkeln mellan vertikal och t_C Det kommer att vara = 180⁰ - 90⁰ - 60⁰ = 30⁰.

Således erhålls det att vinkeln i block k är = (30⁰ + 60⁰)

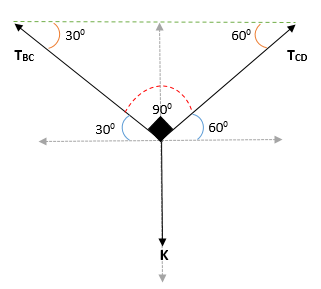
Tillämpa Lamys teorem vid punkt C:

T_{före Kristus}/ sin 150⁰ = B / sin 90⁰

Q = t_{FÖRE KRISTUS *} Sen 90⁰ / sin 150⁰

Q = 240 n * 1/0,5

Q = 480 n.

Referenser

1. Ferdinand p. Öl, e. R. (2013). Mekanik för ingenjörer, statisk. McGraw-Hill Inter-American.
2. Francisco Español, J. C. (2015). Löst linjära algebraproblem. Paraninfo -utgåvor, s.TILL.
3. Graham, j. (2005). Styrka och rörelse. Houchton Mifflin Harcourt.
4. Harpe, s. d. (2000). Ämnen i geometrisk gruppteori. University of Chicago Press.
5. P. En tpler y, g. M. (2005). Fysik för vetenskap och teknik. Volym I. Barcelona: Återgå dig.TILL.