Overlay Theorem Förklaring, applikationer, övningar löst

han Superpositionsteorem, I elektriska kretsar konstaterar den att spänningen mellan två punkter, eller strömmen genom dem, är den algebraiska summan av spänningarna (eller av strömmarna om det är fallet), på grund av varje källa, som om varje verkar i en sätt oberoende.

Detta sats tillåter analys av linjära kretsar som innehåller mer än en oberoende källa, eftersom det endast är nödvändigt att beräkna bidraget från varje separat.

Linjär beroende är avgörande för teoremet att tillämpa. En linjär krets är den vars svar är direkt proportionell mot posten.

Till exempel, Ohms lag som tillämpas på ett elektriskt motstånd, fastställer det V = i.R, var V Det är spänningen, R är motståndet och Yo Det är strömmen. Det är då ett linjärt beroende av spänning och ström i ett motstånd.

I linjära kretsar tillämpas superpositionsprincipen med hänsyn till följande:

-Varje oberoende spänningskälla måste övervägas separat och för detta är det nödvändigt att stänga av alla andra. Det räcker till 0 V alla som inte är under analys eller ersätter dem i schemat med en kortslutning.

-Om källan är måste kretsen öppnas.

-När det inre motståndet hos både ström- och spänskällor beaktas måste dessa förbli på plats, vara en del av resten av kretsen.

-Om det finns beroende källor måste de vara som det visas i kretsen.

[TOC]

Ansökningar

Överlappningsteoremet används för att få enklare och enklare kretsar att hantera. Men det måste hållas i åtanke att endast gäller de med linjära svar, som anges i början.

Då kan den inte användas direkt för att beräkna kraften till exempel, eftersom kraften är relaterad till strömmen genom:

P = i² R

Eftersom strömmen är kvadrat är svaret inte linjärt. Det är inte heller tillämpligt på magnetkretsar där transformatorer ingriper.

Kan tjäna dig: dynamisk el

Å andra sidan ger superpositionsteoremet möjlighet att veta effekten varje källa på kretsen har. Och naturligtvis, genom dess tillämpning är det möjligt att lösa det helt, det vill säga att känna till strömmar och spänningar genom varje motstånd.

Överlappningsteoremet kan också användas i samband med andra kretssatser, till exempel thévenin, för att lösa mer komplexa konfigurationer.

I växlande strömkretsar är också teoremet användbart. I det här fallet arbetar vi med impedanser istället för motstånd, så länge det totala svaret för varje frekvens av oberoende kan beräknas.

Slutligen, i elektroniska system, är teoremet tillämpligt för både direkt och alternativ aktuell analys, separat.

Steg för att tillämpa överlappningsteoremet

-Avaktivera alla oberoende källor efter instruktionerna i början, utom den som ska analyseras.

-Bestäm utgången, antingen spänning eller ström, som producerar den enskilda källan.

-Upprepa de två stegen som beskrivs för alla andra källor.

-Beräkna den algebraiska summan av alla bidrag som finns i föregående steg.

Löst övningar

Exemplen som löstes nedan klargör användningen av teoremet i några enkla kretsar.

- Exempel 1

I den krets som visas i följande figur, hitta strömmen som korsar varje motstånd genom överlappningsteoremet.

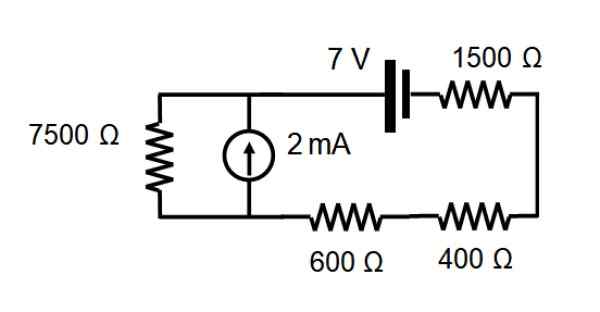
Lösning

Spänningskällbidrag

För att starta den nuvarande källan elimineras, med vilken kretsen förblir på detta sätt:

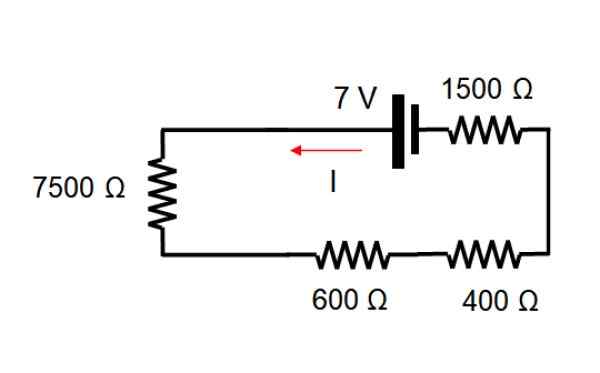
Motsvarande motstånd är att lägga till värdet på varje motstånd, eftersom de alla är i serie:

7500 +600 +400 +1500 Ω = 10.000 Ω

Tillämpa Ohms lag V = i.R Och rensa strömmen:

I = v / r = 7/10.000 A = 0.0007 a = 0.7 ma

Denna ström är densamma för allt motstånd.

Kan tjäna dig: Millikan Experiment: Procedure, Förklaring, betydelse

Bidrag från den nuvarande källan

Spänningskällan elimineras omedelbart, för att bara arbeta med den nuvarande källan. Den resulterande kretsen visas nedan:

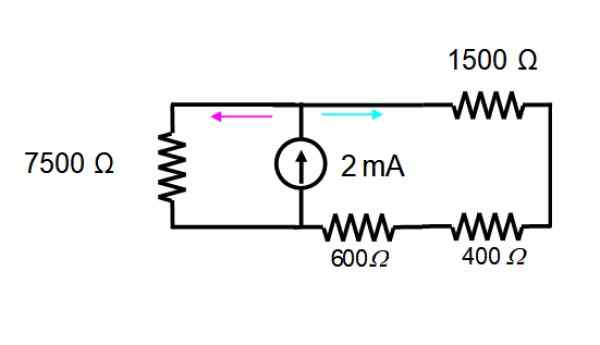
Motståndet i nätet till höger är i serie och kan ersättas av endast en:

600 +400 + 1500 Ω = 2500 Ω

Den resulterande kretsen är så här:

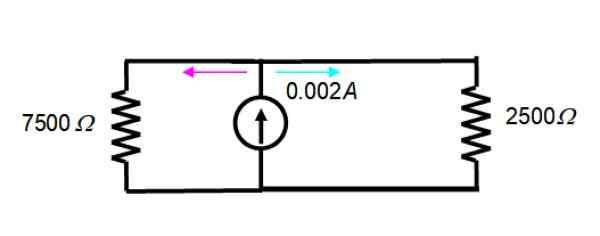
Strömmen på 2 ma = 0.002 A är uppdelat mellan figurens två motstånd, därför är ekvationen för den nuvarande divisorn giltig:

Yo_x = (R_eq/R_x) Yo_T

Var Yo_x är den nuvarande motståndet R_x, R_eq symboliserar motsvarande motstånd och Yo_T är den totala strömmen. Det är nödvändigt att hitta motsvarande motstånd mellan dem, att veta att:

1/r_eq = (1/ r₁) + (1/ r₂)

Därför:

1/r_eq = (1/7500) + (1/2500) = 1/1875 → R_eq = 1875 Ω

För denna andra krets ersätter strömmen som passerar genom motståndet på 7500 Ω värden i den nuvarande delningsekvationen:

Yo_{7500 Ω} = (1875/7500). 0.002 a = 0.0005 A = 0.5 ma

Medan den som passerar genom 2500 Ω -motståndet är:

Yo_{2500 Ω} = 2 ma - 0.5 mA = 1.5 ma

Superposition Theorem Application

Nu appliceras överlappningsteoremet för varje motstånd, börjar med 400 Ω:

Yo_{400 Ω} = 1.5 ma - 0.7 ma = 0.8 ma

Viktig: För detta motstånd subtraheras strömmarna, eftersom de cirkulerar i motsatt riktning, vilket framgår av den noggranna observationen av figurerna, där sinnena i strömmarna har olika färger.

Samma ström går lika med motståndet på 1500 Ω och 600 Ω, eftersom de alla är i serie.

Sedan tillämpas teoremet för att hitta strömmen genom motståndet 7500 Ω:

Yo_{7500 Ω} = 0.7 ma + 0.5 mA = 1.2 ma

Viktig: När det gäller motståndet 7500 Ω, observera att strömmarna tillsätts, för i båda kretsarna cirkulerar de i samma riktning när de passerar genom detta motstånd. Återigen är det nödvändigt att noggrant observera strömmarna i strömmarna.

Kan tjäna dig: relativa fel: formler, hur det beräknas, övningar

- Övning 2

Hitta strömmen och spänningen genom motståndet på 12 Ω genom överlappningsteoremet.

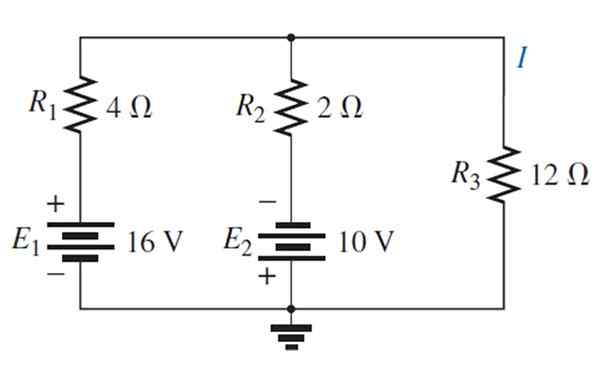
Lösning

Källa E ersätts₁ Med en kortslutning:

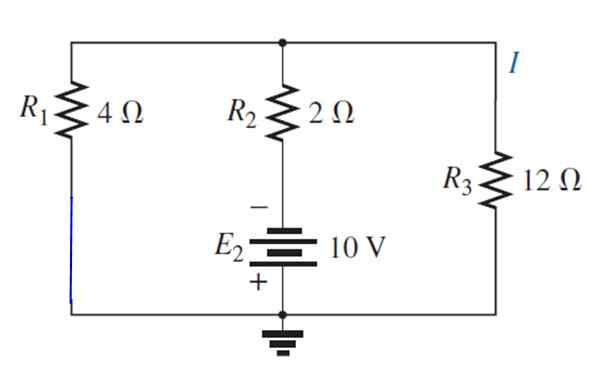
Den resulterande kretsen ritas enligt följande för att enkelt visualisera motstånden som förblir parallellt:

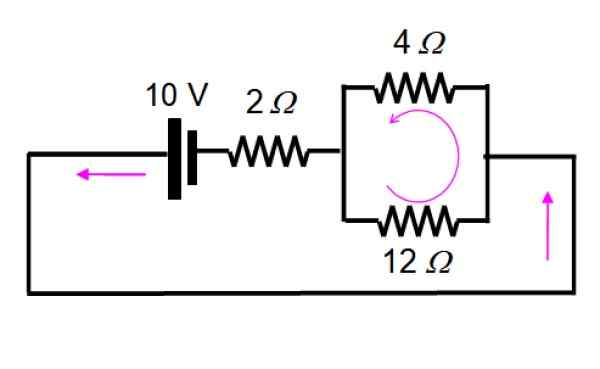
Och nu löses det genom att tillämpa serier och parallella:

1/r_eq = (1/12) + (1/4) = 1/3 → R_eq = 3 Ω

Detta motstånd är i sin tur i serie med det 2 Ω, Därför är det totala motståndet 5 Ω. Den totala strömmen är:

I = v / r = 10 v / 5 Ω = 2 a

Denna ström är uppdelad som:

Yo_12Ω = (3/12) 2 a = 0.5 a

Därför är spänningen:

V_12Ω = 0.5 A × 12 Ω = 6 V

Nu är källan aktiverad₁:

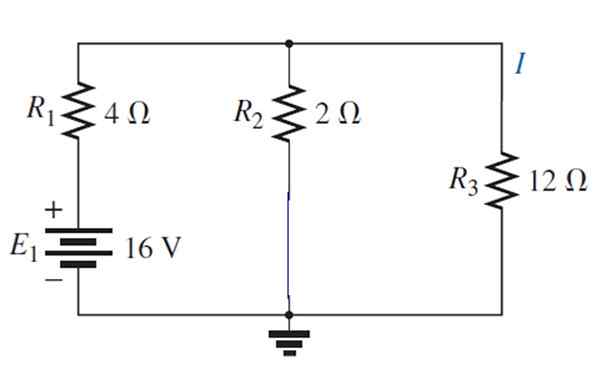
Den resulterande kretsen kan dras på detta sätt:

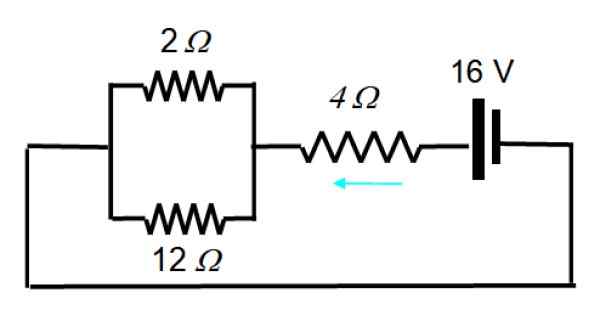
1/r_eq = (1/12) + (1/2) = 7/12 → R_eq = 12/7 Ω

Och i serie med 4 Ω Det är ett motsvarande motstånd 40/7 Ω. I detta fall är den totala strömmen:

I = v/r = 16 V/(40/7) Ω = 14/5 a

Spänningsdelaren med dessa värden appliceras igen:

Yo_12Ω = ((12/7)/12) (14/5) a = 0.4 a

Den resulterande strömmen är: 0.femtio.4 a = 0.1 a. Observera att de har subtraherats, eftersom strömmen för varje källa gör olika betydelser, som kan ses i den ursprungliga kretsen.

Spänningen genom motstånd är:

V_12Ω = 0.4 A × 12 Ω = 4.8 v

Slutligen är den totala spänningen: 6 V-4.8 V = 1.2 v

Referenser

1. Alexander, c. 2006. Elektriska kretsfundament. 3: e. Utgåva. MC Graw Hill.
2. Boylestad, r. 2011. Introduktion till kretsanalys. 2: a. Utgåva. Pearson.
3. Dorf, r. 2006. Introduktion till elektriska cirkuds. 7th. Utgåva. John Wiley & Sons.
4. Edminister, J. nitton nittiosex. Elektriska kretsar. Schaumserie. 3: e. Utgåva. MC Graw Hill
5. Wikipedia. Nuvarande delare. Återhämtat sig från: det är.Wikipedia.org.