Ortogonala matrisegenskaper, demonstration, exempel

Du har en Ortogonal matris När den nämnda matrisen multipliceras med dess transponering resulterar i identitetsmatrisen. Om den inversa av en matris är lika med den transponerade är den ursprungliga matrisen ortogonal.

Ortogonala matriser är karakteristiska att antalet rader är lika med antalet kolumner. Dessutom är radvektorer enhetens ortogonala vektorer och utslaget av transponerade vektorer är också.

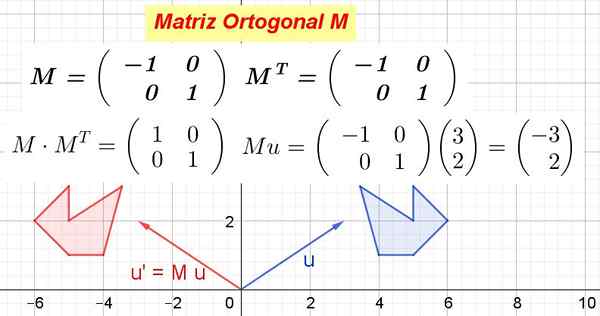Figur 1. Exempel på ortogonal matris och hur förvandlar geometriska objekt. (Förberedd av Ricardo Pérez)

När en ortogonal matris multipliceras med vektorerna i ett vektorutrymme producerar en isometrisk omvandling, det vill säga en omvandling som inte ändrar avstånd och bevarar vinklarna.

En typisk representant för ortogonala matriser är rotationsmatriser. Transformationerna av ortogonala matriser på ett vektorutrymme kallas Ortogonala transformationer.

De geometriska transformationerna av rotation och reflektion av punkter som representeras av dess kartesiska vektorer görs genom att applicera ortogonala matriser på de ursprungliga vektorerna för att erhålla koordinaterna för de transformerade vektorerna. Det är av denna anledning som ortogonala matriser används allmänt vid beräkningsgrafisk bearbetning.

[TOC]

Egenskaper

En matris M Det är ortogonalt om det multipliceras med dess transponering M^T identitetsmatrisen resulterar i Yo. På liknande sätt är produkten av transponering av en ortogonal matris med den ursprungliga matrisen för identitetsmatrisen:

M m^T = M^T M = i

Som en följd av det tidigare uttalandet är införandet av en ortogonal matris lika med dess omvända matris:

M^T = M^-1.

Uppsättningen av ortogonala dimensionsmatriser n x n De bildar den ortogonala gruppen Eller (n). Och delmängden av Eller (n) av ortogonala matriser med bestämning +1 från Special Matrices Group Its (n). Gruppens matriser Din (n) De är matriser som producerar linjära rotationstransformationer, även kända som Rotationsgrupp.

Demonstration

Vi kommer att visa att en matris är ortogonal om, och bara om radvektorerna (eller kolumnvektorerna) är ortogonala för varandra och av norm 1.

Kan tjäna dig: Bayes teorem

Antag att rankningarna för en ortogonal matris n x n är n n ortonormala vektorer av dimension n. Om det betecknas av v1, v2,.. ., vn N -vektorerna är uppfyllda:

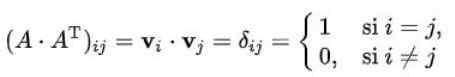
Där det är uppenbart att uppsättningen av radvektorer är en uppsättning ortogonala vektorer med Norm One.

Exempel

Exempel 1

Visa att den 2 x 2 -matrisen som vektorn har i sin första rad V1= (-1 0) och i sin andra rad vektorn V2= (0 1) är en ortogonal matris.

Lösning: Matrisen är byggd M och dess transponering beräknas M^T:

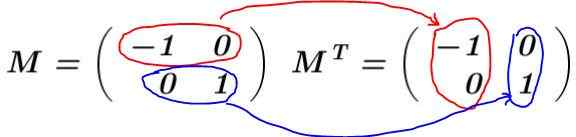
I det här exemplet, matrisen M Det är en transponerad bil, det vill säga att matrisen och dess transponering är identiska. Det multipliceras M för sin transposition M^T:

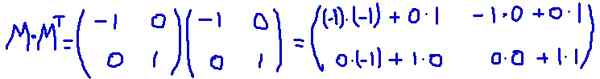
Det verifieras det M M^T Det är lika med identitetsmatrisen:

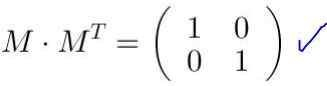
När matrisen M Det multipliceras med koordinaterna för en vektor eller en punkt, nya koordinater erhålls som motsvarar den transformation som matrisen gör på vektorn eller punkten.

Figur 1 visar hur M Förvandlar vektorn eller i eller' Och också gillar M Förvandla den blå polygonen till den röda polygonen. Som M Det är ortogonalt, det är då en ortogonal transformation, som bevarar avstånd och vinklar.

Exempel 2

Antag att du har en 2 x 2 matris definierad i reais som ges av följande uttryck:

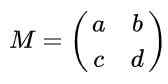
Hitta de verkliga värdena på till, b, c och d så att matrisen M Vara en ortogonal matris.

Lösning: Per definition är en matris ortogonal om den multipliceras med dess transponering erhålls som ett resultat av identitetsmatrisen. Att komma ihåg att den transponerade matrisen erhålls från originalet är utbyte av rader med kolumner följande jämlikhet:

Det kan tjäna dig: domän och motsägelse av en funktion (med exempel)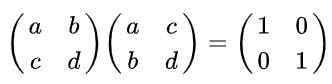

Att utföra matrismultiplikationen är:

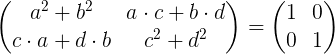
Genom att jämföra elementen i den vänstra matrisen med elementen i identitetsmatrisen till höger, får vi ett system med fyra ekvationer med fyra okända A, B, C och D.

Vi föreslår för A, B, C och D Följande uttryck baserade på trigonometriska skäl till sinus och kosinus:

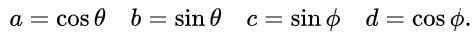
Med detta förslag och på grund av den grundläggande trigonometriska identiteten är den första och den tredje ekvationen i jämställdhet mellan matriselementen automatiskt nöjd. Den tredje och fjärde ekvationen är densamma och i matrisjämlikhet efter att de föreslagna värdena är så här:

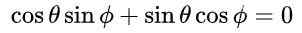
vilket leder till följande lösning:

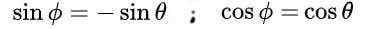
Slutligen erhålls följande lösningar för den ortogonala matrisen M:

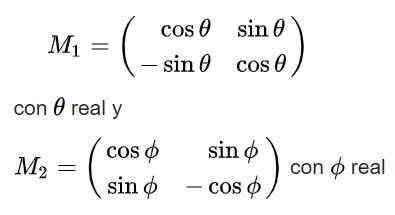
Observera att den första av lösningarna har en determinant +1 så att den tillhör dess grupp (2), medan den andra lösningen har en determinant -1 och därför inte tillhör denna grupp.

Exempel 3

Med tanke på följande matris, hitta värdena på A och B för att ha en ortogonal matris.

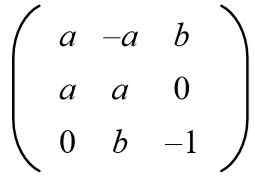
Lösning: För att en given matris ska vara ortogonal måste produkten med sin transponering vara identitetsmatrisen. Sedan görs matrisprodukten från matrisen som ges med dess transponerade matris och ger följande resultat:

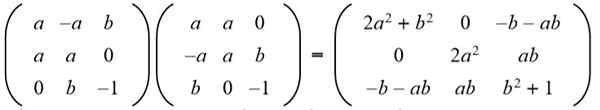
Därefter matchas resultatet med identitetsmatrisen 3 x 3:

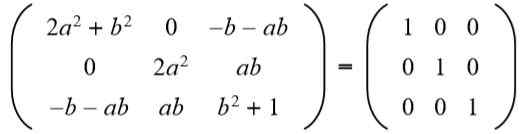
I den andra raden tredje kolumnen har du (A B = 0), men till Det kan inte vara noll, för i så fall skulle jämställdheten mellan elementen i den andra raden och andra kolumnen inte uppfyllas. Då nödvändigtvis B = 0. Byter ut b För värdet 0 har vi:

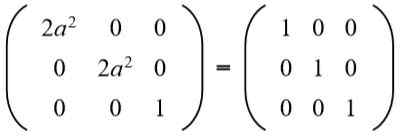
Då löses ekvationen: 2a^2 = 1, vars lösningar är: +½√2 och -½√2.

Kan tjäna dig: typer av vinklar, egenskaper och exempel

Tar den positiva lösningen till till Det resulterar i följande ortogonala matris:

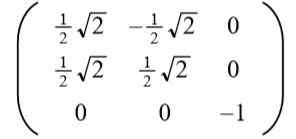
Läsaren kan enkelt verifiera att raderna vektorer (och även kolumnvektorer) är ortogonala och enhet, det vill säga.

Exempel 4

Visa att matrisen TILL vars rader är V1 = (0, -1 0), V2 = (1, 0, 0) och V3 = (0 0 -1) Det är en ortogonal matris. Hitta dessutom hur vektorerna i den kanoniska basen förvandlas I J K Till vektorerna U1, U2 och U3.

Lösning: Det bör komma ihåg att elementet (i, j) av en matris multiplicerad med dess transponering, är den skalära produkten från vektorn av rad (i) av kolumnen (j) för transponeringen. Dessutom är denna produkt lika med Kronecker's Delta om matrisen är ortogonal:

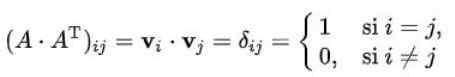
I vårt fall är det så här:

V1 • v1 = 0x0 + (-1) x (-1) + 0x0 = 1

V2 • v2 = 1 × 1 + 0x0 + 0x0 = 1

V3 • V3 = 0x0 + 0x0 + (-1) x (-1) = 1

V1 • v2 = 0x1 + (-1) x0 + 0x0 = 0

V2 • v1 = 1 × 0 + 0x (-1) + 0x0 = 0

V2 • v3 = 1 × 0 + 0x (0) + 0x (-1) = 0

V3 • V2 = 0x1 + 0x (0) + (-1) x0 = 0

V1 • v3 = 0x0 + (-1) x (0) + 0x (-1) = 0

V3 • v1 = 0x0 + 0x (-1) + (-1) x0 = 0

Med vad som visas att det är en ortogonal matris.

Förutom u1 = a i = (0, 1, 0); U2 = A J = (-1, 0, 0) och slutligen U3 = a k = (0, 0, -1)

Referenser

1. Anthony Nicolaides (1994) Determinants & Matrices. Godkänd publicering.
2. Birkhoff och maclane. (1980). Modern Algebra, ed. Vicens-Vives, Madrid.
3. Casteleiro villalba m.  (2004) Introduktion till linjär algebra. ESIC -redaktion.
4. Dave Kirkby (2004) Maths Connect. Heinemann.
5. Jenny Olive (1998) Maths: A Student's Survival Guide. Cambridge University Press.
6. Richard J. Brown (2012) 30-sekunders matematik: De 50 mest mind-expanderande teorierna i matematik. Ivy Press Limited.
7. Wikipedia. Ortogonal matris. Återhämtad från: är.Wikipedia.com
8. Wikipedia. Ortogonal matris. Hämtad från: i.Wikipedia.com