Förklaringsfaktorsteorem, exempel, övningar

han faktorsats säger att en polynom P (x) är delbar med en binomial av formen (x - a) om x = a är en rot till p (x), det vill säga p (a) = 0. Det sägs att ett polynom är delbart bland en annan när dess rest eller vila är noll.

Ett polynom är ett uttryck för form:

P (x) = a_n xⁿ + till_N-1 x^N-1 +... + a₁ x + a₀

Figur 1. Faktorsats. Källa: f. Zapata.

Var:

-n är graden av polynom och är det största heltalsnumret som den oberoende variabeln x stiger,

-Värden a_n, till_N-1 ,... + a₁ , till₀ De är koefficienterna för polynomet, som i allmänhet är verkliga siffror, men de kan också vara komplexa siffror.

En klass N -polynom kan sönderdelas som produkt från Binomials:

(X - r_Yo)

Där r_Yo Det är den i-alkiska P (x) roten:

P (x) = a_n (X - r₁) (X - r₂) ... (x - r_n)

Eftersom antalet rötter av ett polynom är lika med graden av samma.

[TOC]

Exempel

- Exempel 1

Tänk på polynomet i fall:

P (x) = 3⋅x² - 7⋅x + 2

Du vill veta om detta polynom är delbart med binomialen (x - 2). Om faktorteoremet används, måste vi utvärdera p (x = 2) för att veta om värdet 2 är en rot eller inte. Vi fortsätter sedan att utvärdera uttrycket:

P (2) = 3⋅22 - 7⋅2 + 2 = 3⋅4 - 7⋅2 + 2 = 12 - 14 + 2 = 12 - 12 = 0.

Det visar sig att x = 2 är p (x) rot, så enligt faktorteoremet är binomialen (x - 2) verkligen en faktor av p (x).

Låt oss gå vidare till direkt verifiering som gör divisionen. Detaljen i hur uppdelningen görs visas i följande figur:

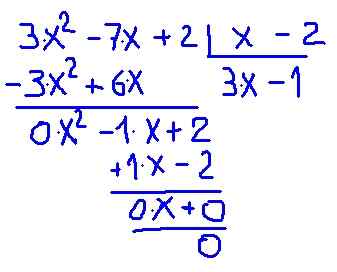figur 2.- Polynomavdelning P (x) mellan binomial x-2. Källa: f. Zapata.

Det verifieras att kvoten mellan p (x) och (x -2) ger ett polynom av en mindre grad som kallas kvoten c (x) = 3⋅x - 1 med rest 0.

Kan tjäna dig: vektorfunktioner

Vi kan sammanfatta resultatet enligt följande:

(3⋅x² - 7⋅x + 2) ÷ (x -2) = (3⋅x - 1) + 0

Det föregående uttrycket kan skrivas på ett annat sätt, helt enkelt komma ihåg att utdelningen p (x) är lika med produkten från divisorn (x -2) med kvoten (3⋅x - 1) plus återstoden (noll i detta fall ):

(3⋅x² - 7⋅x + 2) = (x -2) (3⋅x - 1) + 0

På detta sätt skrivs P (x) polynomet (x), det vill säga som en produkt av polynomer, det ursprungliga polynomet: det ursprungliga polynomet:

(3⋅x² - 7⋅x + 2) = (x -2) (3⋅x - 1)

- Exempel 2

Vara polynomet q (x) = x³ - x + 2. Du vill veta om det är delbart med binomialen (x + 1).

Det mest direkta sättet är helt enkelt att tillämpa faktorteoremet. I det här fallet måste du helt enkelt verifiera om x = -1 annuler eller inte polynomet q (x).

Vi fortsätter genom att ersätta:

Q (-1) = (-1)³ - (-1) + 2 = -1 + 1 + 2 = 2

Resultatet skiljer sig från noll, därför säkerställer faktorsteoremet att polynomet Q (x) inte är delbar mellan (x + 1), eftersom q (-1) ≠.

Nu kommer uppdelningen av Q (x) att göras mellan binomialen (x + 1) som en metod för verifiering av vår slutsats.

Vid detta tillfälle kommer divisionen att genomföras genom den syntetiska uppdelningsmetoden, som består av att placera i den övre delen av första klass alla koefficienterna för polynomet, inklusive de saknade, eftersom de har nollkoefficient.

Sedan i den första kolumnen placeras den oberoende termen för divisorn men med skylten ändras, i vårt fall är divisorn (x + 1). Dess oberoende term är 1, men som i den första kolumnen är den placerad ändrad tecken, det vill säga -1.

Följande figur illustrerar hur den syntetiska uppdelningen genomförs:

Kan tjäna dig: polynomiska ekvationer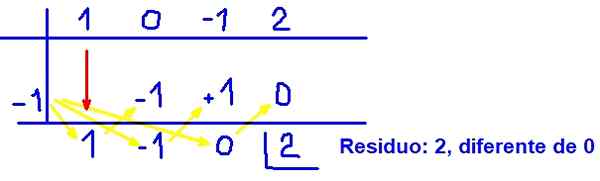Figur 3. Exempel på polynom syntetisk uppdelning. Källa: f. Zapata.

Med detta resultat har det bevisat att (x + 1) det inte är en faktor för polynom q (x) = x³ - x + 2 Eftersom återstoden inte är noll.

Denna slutsats är inte förvånad, eftersom den redan hade förutses med faktorteoremet. Observera att vid ersättning av x = -1 i q (x) är det som erhålls just resterna eller resten av polynomavdelningen, eftersom q (-1) = rest = 2.

Naturligtvis tillhandahåller divisionen ytterligare information om kvoten C (x) = x² - x.

Kom ihåg att utdelningen Q (x) är lika med divisorn (x + 1) med förhållande c (x) plus resten r = 2 Vi har utvidgningen av polynomet Q (x) enligt följande:

Q (x) = (x + 1) (x² - x) + 2 = x (x + 1) (x - 1) + 2

Det bör noteras att detta uttryck inte är faktoriseringen av nämnda polynom, eftersom det finns en icke -noll term som läggs till, vilket är just värdet på värde 2.

Övningar

- Övning 1

Hitta polynomfaktorerna

P (x) = x³ - 5 x² + 2 x + 8

Och skriv också din faktorisering.

Lösning

Faktorsteoremet indikerar att vi måste leta efter rötter till och sedan hitta faktorerna (x - till), I det här fallet, eftersom det är en grad tre polynom, måste det finnas tre rötter. 

Eftersom det är ett polynom med hela koefficienter, måste rötterna vara bland delarna av den oberoende termen som i detta fall är 8. Dessa delare är:

± 1, ± 2, ± 4, ± 8.

Vi börjar med att utforska +1: p (+1) = 1³ - 5⋅ 1² + 2⋅1 + 8 = 1 - 5 + 2 + 8 = 6 som skiljer sig från 0, därför är +1 inte rot.

Vi utforskar -1:

P (-1) = (-1)³ - 5⋅ (-1)² + 2⋅ (-1) + 8 = -1 - 5 - 2 + 8 = 0

Från resultatet dras slutsatsen att -1 är roten till p (x) y (x -( -1)) = (x + 1) är en polynomfaktor.

Kan tjäna dig: minsta rutor

Vi måste hitta ytterligare två faktorer:

Vi försökte nästa som är +2:

P (+2) = (+2)³ - 5⋅ (+2)² + 2⋅ (+2) + 8 = 8 + (-20) + 4 + 8 = 0

Återigen får vi noll. Då är den andra faktorn (x - 2).

Eftersom det är en grad tre polynom behöver vi bara hitta en faktor. Nu försökte vi +4 -värdet för att veta om polynomet avbryter:

P (+4) = (+4)³ - 5⋅ (+4)² + 2⋅ (+4) + 8 = 64 - 80 + 8 + 8 = 0.

Med andra ord.

Du behöver inte fortsätta leta efter, för det är ett klass 3 -polynom som har högst tre rötter. I denna övning visade sig alla rötter vara verkliga och hela.

Därför är polynomet p (x) faktor som denna:

P (x) = x³ - 5 x² + 2 x + 8 = (x + 1) (x - 2) (x - 4).

- Övning 2

Vara p⋅x -polynomet³ - x + 2p. Bestäm värdet på P för att polynom ska delas med (x + 2).

Lösning

Vi använder faktorteoremet, som säger att om x = -2 avbryter polynomet då (x -( -2)) är en faktor för nämnda polynomialt.

Sedan ersätts x av (-2) i det ursprungliga polynomet, det förenklas och är lika med noll:

P⋅ (-2)³ - (-2) + 2p = 8p + 2 + 2p = 10p + 2 = 0

Nu rensas värdet på P så att jämlikhet uppfylls till noll:

P = -2 / 10 = -⅕ 

Detta betyder att polynom: 

-⅕⋅x³ - X - ⅖

Det är delbart med (x + 2), eller vad som är motsvarande: (x + 2) är en av dess faktorer.

Referenser

1. Baldor Aurelio. Algebra. Patria Redaktionsgrupp.
2. Demana, w. Precáculculo: grafik, numerisk, algebraisk 7: e ed. Pearson Education.
3. Jiménez, r. 2008. Algebra. Prentice hall.
4. Stewart, J. 2006. Preccculment: Matematik för beräkning. Femte. Utgåva. Cengage Learning.
5. Zill, D. 1984. Algebra och trigonometri. McGraw Hill.