Tredje lagen i termodynamikformler, ekvationer, exempel

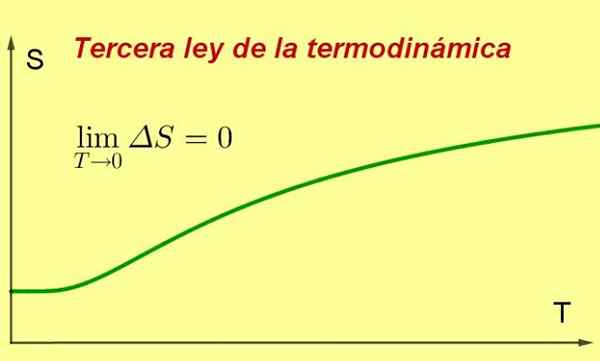
De Tredje lagen om termodynamik säger att entropin av ett stängt termodynamiskt system i jämvikt tenderar att vara minimal och konstant, när temperaturen närmar sig 0 kelvin.

Detta värde på entropi kommer att vara oberoende av systemvariablerna (trycket eller det applicerade magnetfältet, bland andra). Vad som händer är att när temperaturen är närmare 0 K stoppas processerna i systemet och hur entropi är ett mått på intern agitation, det går nödvändigtvis ner.

Figur 1. När temperaturen i ett system närmar sig den absoluta nollet når dess entropi ett minimum och konstant värde. Källa: Utarbetad av F. Zapata ..

[TOC]

Tidigare koncept

För att förstå omfattningen av den tredje lagen om termodynamik, relevant för mycket låga temperaturer, är det nödvändigt att granska följande koncept:

Termodynamisk system

Det hänvisar vanligtvis till en gas, en vätska eller en fast. Vad som inte är en del av systemet kallas runt. Det vanligaste termodynamiska systemet är den perfekta gasen, som består av N -partiklar (atomer) som endast interagerar genom elastiska kollisioner.

Isolerade, stängda eller öppna system

Isolerade system är inte tillåtna något utbyte med miljön. Stängda system utbyter inte materia med miljön utan värme. Slutligen kan öppna system byta både materia och värma med miljön.

Makrostat och mikrostata

Makrostaten för ett system är uppsättningen värden som har sina variabler: tryck, temperatur, volym, antal mol, entropi och inre energi. Å andra sidan, mikro -eventem -i fallet med en idealisk gas -ges av positionen och momentumet för var och en av n -partiklarna som utgör det, vid ett visst ögonblick. 

Många mikrostater kan resultera i samma makrostat. I en gas vid rumstemperatur är antalet möjliga mikrostatar enormt, eftersom antalet partiklar som utgör det, de olika positionerna och de olika energierna de kan anta är mycket stort. 

Formler och ekvationer

Entropi är en termodynamisk makroskopisk variabel som mäter systemet med molekylstörning i systemet. Graden av störning i ett system är större i den utsträckning som antalet möjliga mikrostater är större. 

Detta koncept behövs för att formulera den tredje lagen om termodynamik i matematisk form. Vare sig det är entropin i systemet, då:

Detta innebär att entropi i ett stängt system inte förändras när dess temperatur t tenderar att absolut noll.

Entropi är en makroskopisk tillståndsvariabel som är direkt relaterad till antalet möjliga mikrostat i ett system, med hjälp av följande formel:

S = k ln (w)

I föregående ekvation: S representerar entropi, W antalet möjliga mikrostater i systemet och k Det är Boltzmanns konstant (K = 1.38 x 10^-23 J/k). Det vill säga, entropin för ett system är k gånger den naturliga logaritmen för antalet möjliga mikrostater.

Beräkning av det absoluta entropin

Det är möjligt att definiera den absoluta entropin av ett rent ämne baserat på definitionen av variationen i entropi:

Där Δq är den oändliga variationen av värme och t är temperaturen. Denna ekvation är giltig om processen är reversibel (rev).Om det är en isobarisk - konstant tryckprocess kan värmen som byts ut under en oändlig temperaturvariation skrivas så här:

Δq = n . c_p .Dt

Här är CP den specifika molvärmen och n antalet mol. Molarspecifikt värmeberoende med temperatur är ett experimentellt erhållet faktum och är känt för många rena ämnen.

Kan tjäna dig: Solsystem: Planeter, egenskaper, ursprung, evolution

Enligt den tredje lagen i rena ämnen: 

Så absolut entropi av en mol av rent ämne som:

I föregående notation indikerar stången att det är entropin för en mol av substans och Superson º betecknar ett rent ämne.

Ansökningar

I det dagliga livet har den tredje lagen om termodynamik få tillämpningar, helt i strid med den första och andra lagen. Det beror på att det är en princip som hänvisar till vad som händer i ett system när det närmar sig det absoluta 0, en rang av sällsynta temperaturer.

I själva verket når det absoluta eller −273,15 ° C omöjligt (se exempel 1 senare) Men den tredje lagen tillämpas när man studerar materialets svar vid mycket låga temperaturer. 

Tack vare detta har viktiga framsteg i kondenserade ämnen dykt upp, till exempel:

-Superfluiditet (se exempel 2 senare)

-Superledningsförmåga 

-Laserkylningstekniker 

-Bose-Einstein kondensat 

-Fermi överflödiga gaser.

figur 2. Överflödig flytande helium. Källa: Wikimedia Commons.

Vid extremt låga temperaturer tillåter nedstigningen av entropi uppkomsten av intressanta kvantfenomen. Låt oss därför se vad som händer med entropin i ett mycket lågt temperatursystem.

Entropi av ett lågtemperatursystem

När du har ett perfekt kristallint ämne är dess minsta entropi exakt noll, eftersom det är en mycket snygg. I temperaturer nära Absolut.

Vissa författare överväger ett alternativt uttalande om den tredje lagen om termodynamik följande:

"Om materien kondenserar en perfekt kristall, när temperaturen tenderar att absolut noll, tenderar entropi exakt till noll". 

Låt oss puntera vissa aspekter av det föregående uttalandet: 

- En perfekt kristall är en där varje molekyl är identisk och där molekylstrukturen upprepas identiskt i sin helhet.

- När temperaturen tenderar att absolut noll minskar atomvibrationer nästan fullständigt.

Sedan bildar glaset en enda möjlig konfiguration eller mikrouttalande, det vill säga W = 1, Och därför är entropi lika med noll:

 S = k ln (1) = 0

Men inte så länge ett material som kyls nära den absoluta noll bildar en kristall, mycket mindre är denna kristall perfekt. Detta inträffar endast om kylningsprocessen är mycket långsam och reversibel.

Annars skulle faktorer som föroreningar som finns i glaset möjliggöra förekomsten av andra mikrostater. Därför skulle W> 1 och entropi vara större än 0.

Återstående entropi

Om kylningsprocessen är plötsligt, under samma sak går systemet genom en följd av icke -balansstater, vilket leder till att materialet ska visas. I det här fallet finns det ingen kristallin och ordnad struktur, utan ett amorft fast ämne, vars struktur liknar en vätska. 

I så fall är det minsta entropivärdet i närheten av absolut noll inte noll, eftersom antalet mikrostater är mycket större än 1. Skillnaden mellan denna entropi och nollentropin i det perfekta kristallina tillståndet kallas återstående entropi.

Förklaringen är att systemet under en viss tröskeltemperatur har ingen annan möjlighet än ockupationen.

Det kan tjäna dig: första lagen om termodynamik: formler, ekvationer, exempel

De kommer att ansvara för att upprätthålla konstant entropi, även om temperaturen fortsätter att gå ner mot absolut noll.

Exempel

Exempel 1: Det absoluta nollet och obestämningen av Heisenberg

Heisenberg -obestämdhetsprincipen konstaterar att osäkerheten i en partikelens position och fart, till exempel i atomerna i ett kristallint nätverk, inte är oberoende av det andra, utan följer följande ojämlikhet:

Δx ⋅ ΔP ≥ h

Där h är Plancks konstant. Det vill säga osäkerheten i positionen multiplicerad genom osäkerhet i momentumet (massa per hastighet) är större än eller lika med Planck -konstanten, vars värde är mycket litet, men inte noll: H = 6.63 x 10-3. 4 J · s.

Och vad har osäkerhetsprincipen att göra med den tredje lagen om termodynamik? Om positionen för atomerna i det kristallina nätverket är fast och exakt (Δx = 0) Då kan hastigheten på dessa atomer ta vilket värde som helst mellan 0 och oändligheten. Detta motsägs av det faktum att i absolut noll upphör varje rörelse av termisk agitation.

Ömsesidigt, om vi börjar det vid absolut noll av temperaturen, upphör all agitation och momentumet för varje atom i nätverket exakt noll (ΔP = 0), då skulle osäkerhetsprincipen för Heisenberg innebära att obestämdheten i positionerna för varje atom skulle vara oändlig, det vill säga de kan vara i vilken position som helst. 

Som en följd av det föregående uttalandet skulle antalet mikrostater tenderar att oändliga och entropi också skulle ta ett obestämt värde. 

Exempel 2: Superfluiditet och det konstiga fallet med helium-4

I överflödighet, som inträffar vid mycket låga temperaturer, förlorar materien inre friktion mellan dess molekyler, kallad gegga. I detta fall kan vätskan cirkulera utan friktion för alltid, men problemet är vid dessa temperaturer nästan ingenting är flytande utom helium.

Helium och helium 4 (dess vanligaste isotop) utgör ett unikt fall, eftersom vid atmosfärstrycket och vid temperaturer nära absolut noll förblir heliumet flytande. 

När helium-4 skickas in vid en temperatur under 2.2 K vid atmosfärstrycket blir en överflödig. Denna upptäckt inträffade 1911 i Leyden av den nederländska fysikern Heike Kamerlingh Onnes (1853-1926).

Figur 3. Holländsk fysiker Heike Kamerlingh Onnes (1853-1926). Källa: Wikimedia Commons.

Helio-4 Atom är en Boson. Bosoner, till skillnad från fermioner, är partiklar som kan uppta alla samma kvanttillstånd. Därför uppfyller bosoner inte Paulis uteslutningsprincip.

Sedan alla helium-4-atomer vid temperaturer under 2.2 K upptar samma kvanttillstånd och därför finns det inget annat än en enda möjlig mikrostata, vilket innebär att överflödig helium-4 har S = 0.

Löst övningar

- Övning 1

Tänk på ett enkelt fall som består av ett system som endast bildats av tre partiklar som har tre energinivåer. För detta enkla system:

a) Bestäm antalet mikrostat som är möjliga för tre temperaturintervall:

-hög 

-Halv 

-Låg

b) Bestäm genom Boltzmann -ekvationens entropi i de olika temperaturområdena. 

c) Diskutera resultaten och förklara om termodynamikens tredje lag är tredje lagen eller inte.

Lösning till

På en molekylär och atomisk skala kvantiseras de energier som ett system kan anta, vilket innebär att endast vissa diskreta värden kan ta. Dessutom, när temperaturen är så låga, har partiklarna som utgör systemet bara möjligheten att ockupera mindre energinivåer. 

Det kan tjäna dig: magnetisk induktion: formler, hur det beräknas och exempel

Hög temperatur

Om systemet har en relativt hög temperatur, har partiklarna tillräckligt med energi för att ockupera tillgängliga nivåer, vilket ger upphov till 10 möjliga mikrostater, som visas i följande figur:

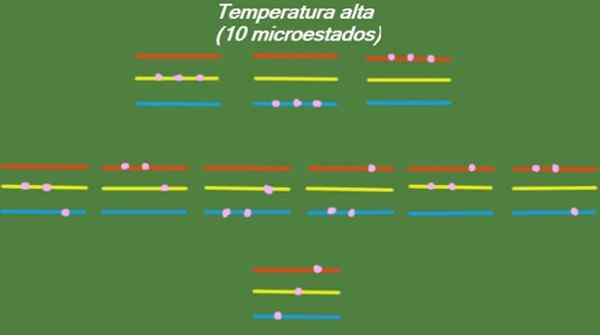Figur 4. Möjliga tillstånd vid hög temperatur för året löst 1. Källa: Utarbetad av F. Zapata.

Medellång temperatur

Om systemet har en mellanliggande temperatur, har de partiklar som utgör det inte tillräckligt med energi för att ockupera den högsta energinivån. De möjliga mikrostaterna illustreras i figuren:

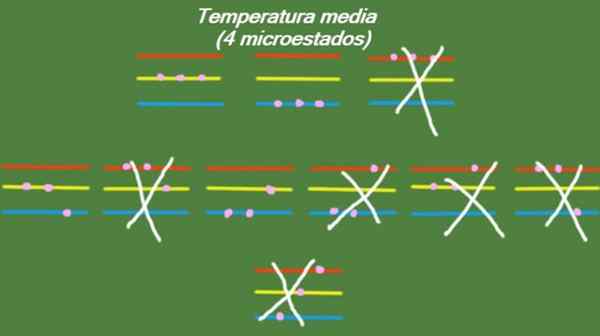Figur 5. Mikrostat vid medeltemperatur för det lösta träningssystemet 1. Källa: Utarbetad av F. Zapata.

Låg temperatur

Om temperaturen fortsätter att gå ner i våra idealiserade tre partiklar och tre energinivåer, kommer partiklarna att ha så liten energi att de bara kan ockupera den lägsta nivån. I detta fall finns det bara en möjlig mikrostata, vilket kan ses i figur 6:

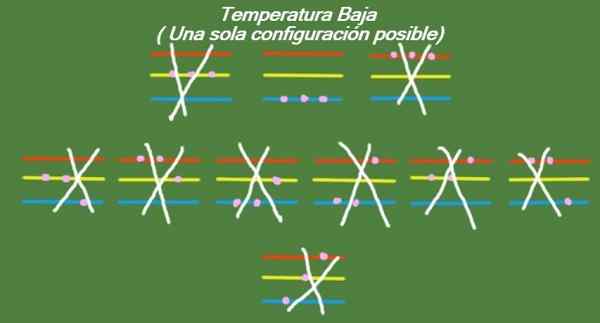Figur 6. Vid låg temperatur finns det en möjlig konfiguration (egen utarbetande)

Lösning B

Redan känt antalet mikrostater i varje temperaturområde, kan vi redan använda Boltzmann -ekvationen som ges tidigare för att hitta entropi i varje fall.

S = k ln (10) = 2.30 x k = 3.18 x 10-23 J/k (Hög temperatur)

S = k ln (4) = 1.38 x k = 1.92 x 10-23 J/k (Medium temperatur)

Och slutligen:

S = k ln (1) = 0 (Låg temperatur)

Lösning C

För det första märker vi att entropin minskar när temperaturen sjunker, som förväntat. Men för de lägsta temperaturvärdena uppnås ett tröskelvärde, från vilket systemets basstatus uppnås.

Även om temperaturen är så nära som möjligt till absolut noll finns det inga mindre tillstånd tillgängliga. Sedan upprätthåller entropin sitt ständiga minimivärde, vilket i vårt exempel är s = 0.

Denna övning illustrerar, på nivån för mikrostaterna i ett system, orsaken till att den tredje lagen om termodynamik uppfylls.

- Övning 2

Anledning om nästa uttalande är sant eller falskt:

"Entropin för ett system vid den absoluta temperaturen noll är exakt noll".

Motivera svaret och beskriv några exempel.

Lösning

Svaret är: falskt.

Först och främst kan inte den absoluta temperaturen uppnås eftersom principen om osäkerhet i Heisenberg och den tredje lagen om termodynamik skulle kränkas. 

Det är mycket viktigt att observera att det i den tredje lagen inte sägs vad som händer i absolut 0, men när temperaturen är oändligt nära den absoluta 0. Skillnaden är subtil, men betydande.

Den tredje lagen bekräftar inte att när temperaturen tar ett värde godtyckligt nära absolut noll, tenderar entropi att noll. Detta skulle hända endast i det tidigare analyserade fallet: den perfekta kristallen, som är en idealisering.

Många mikroskopiska skalasystem, det vill säga i kvantskala, har sin energibasnivå degenererad, Vad betyder förekomsten av flera konfigurationer på den lägsta energinivån. 

Ovanstående betyder att entropi i dessa system aldrig skulle vara exakt noll. Inte heller skulle entropi vara exakt noll i system som är förgyllda när temperaturen tenderar att absolut noll. I det här fallet återstående entropi Före sett.

Det beror på att deras molekyler var "fastna" innan de upptar de lägsta tillgängliga nivåerna av energi, vilket avsevärt ökar antalet möjliga mikrostata, vilket gör det omöjligt att entropi är exakt noll.

Referenser

1. Cengel och. 2012. Termodynamik. Sjunde upplagan. McGraw Hill. 347.
2. Jetipopulsionslaboratorium. Den coolaste platsen i universum. Återhämtat sig från: coldatomlab.Jpl.pott.Gov.
3. González, a. Entropi och spontanitet. Återhämtat sig från: geocities.Ws
4. Quora. Vad är den praktiska användningen av tredje lagen om termodynamik?. Återhämtat sig från: quora.com
5. Allmän kemi. Tredje principen för termodynamik. Återhämtat sig från: Korint.PUCP.Edu.pe
6. Tredje lagen om termodynamik. Återhämtat sig från: YouTube.com
7. Wikipedia. Återstående entropi. Hämtad från: i.Wikipedia.com
8. Wikipedia. Tredje lagen om termodynamik. Hämtad från: i.Wikipedia.com