Newtons tredje lagapplikationer, experiment och övningar

De Newtons tredje lag, även kallad Handlingslag och reaktion Han bekräftar att när ett objekt utövar styrka över en annan, utövar den senare också en kraft med lika stor storlek och riktning och motsatt känsla.

Isaac Newton släppte sina tre lagar 1686 i sin bok Philosophiae Naturalis Principia Mathematica eller matematiska principer för naturfilosofi.

En rymdraket får den nödvändiga framdrivningen tack vare gaserna som utvisas. Källa: Pixabay.

[TOC]

Förklaring och formler

Den matematiska formuleringen av Newtons tredje lag är mycket enkel:

F₁₂ = -F_tjugoett

En av krafterna kallas handling Och den andra är reaktion. Det är emellertid nödvändigt att lyfta fram vikten av denna detalj: båda agerar på olika objekt. De gör det också samtidigt, även om denna terminologi felaktigt antyder att handlingen inträffar före och reaktionen efter.

Eftersom krafter är vektorer, betecknas de med djärva. Denna ekvation indikerar att det finns två objekt: objekt 1 och objekt 2. Kraften F₁₂ Det är den som utövar objekt 1 på objekt 2. Kraften F_tjugoett utövas av objekt 2 på objekt 1. Och tecknet (-) påpekar att de är emot.

När man noggrant observerar Newtons tredje lag är det en viktig skillnad med de två första: medan de åberopar ett enda objekt hänvisar den tredje lagen till två olika objekt.

Och om du tänker noggrant kräver interaktioner par av objekt.

Det är därför krafterna av handling och reaktion inte avbryts eller balanseras, även om de har samma storlek och riktning, men annars: de appliceras i olika kroppar.

Ansökningar

Bollinteraktion - jorden

Här är en mycket daglig tillämpning av en interaktion relaterad till Newtons tredje lag: en boll som faller vertikalt och jorden. Bollen faller till marken eftersom jorden utövar en attraktionskraft, som kallas tyngdkraft. Denna kraft får bollen att falla med konstant acceleration på 9.8 m/s².

Men nästan ingen tänker på det faktum att bollen också utövar en attraktionskraft på jorden. Naturligtvis förblir jorden oföränderlig, eftersom dess massa är mycket större än bollen och därför upplever en föraktlig acceleration.

En annan anmärkningsvärd fråga om Newtons tredje lag är att kontakten mellan de två objekten som interagerar inte är nödvändig. Det framgår av exemplet som just har citerats: bollen tar fortfarande inte kontakt med jorden, men ändå utövar den sin attraktion ändå. Och bollen på jorden också.

En kraft som tyngdkraft, som fungerar omväxlande både om det finns kontakt mellan objekt som om det inte finns något namn på "Distance Action Force". Istället krafter som friktion och normalt, de kräver att föremålen som interagerar är i kontakt, så de kallas "kontaktkrafter".

Formler extraherade från exemplet

Återvända till paret av bollobjekt - Jorden, att välja p -priser för bollen och T för jorden och tillämpa Newtons andra lag för varje deltagare i detta system erhålls:

Det kan tjäna dig: diskret variabel: egenskaper och exempel

F_resulterande = m.till

Den tredje lagen säger att:

m_Ptill_P = - m_Ttill_T

till_P = 9.8 m/s² riktad vertikalt ner. Eftersom denna rörelse äger rum längs den vertikala riktningen kan fördelas med vektorotationen (BOLD); Och att välja riktningen upp så positiv och ner som negativ, du har:

till_P = 9,8 m/s²

m_T ≈ 6 x 10 ²⁴ Kg

Oavsett bollens massa är jordens acceleration noll. Det är därför det observeras att bollen faller mot jorden och inte vice versa.

En raket

Rockets utgör ett bra exempel på tillämpning av Newtons tredje lag. Raketen som visas i bilden i början stiger tack vare framdrivningen av varm gas med hög hastighet.

Många tror att detta händer eftersom dessa gaser på något sätt "stöder" atmosfären eller på marken för att stödja och trycka på raketen. Det fungerar inte så.

När raketen utövar styrka på gaserna och utvisar dem tillbaka, utövar gaserna en kraft på raketen, som har samma modul, men motsatt riktning. Denna kraft är den som ger raketen sin acceleration.

Om du inte har en raket av dessa för hand finns det andra sätt att verifiera att Newtons tredje lag arbetar för att ge framdrivning. Vattenraketer kan byggas, där den nödvändiga drivkraften erbjuds av vattnet per tryckgas.

Det bör noteras att starten av en vattenraket tar tid och kräver många försiktighetsåtgärder.

Skridskor

Ett mer prisvärt och omedelbart sätt att verifiera effekten av Newtons tredje lag är att sätta ett par skridskor och främja en vägg.

För det mesta är förmågan att utöva kraft med föremål som är i rörelse associerad, men sanningen är att orörliga föremål också kan utöva styrka. Skateren drivs tillbaka tack vare den kraft som den rörliga utövar på den.

Kontaktytor utövar kontaktkrafter (normala) med varandra. När en bok stöds på ett horisontellt bord utövar den en normal vertikal kraft på den. Boken utövar på tabellen en vertikal kraft av samma numeriska värde och motsatt mening.

Barnsexperiment: åkare

Barn och vuxna kan uppleva Newtons tredje lag och verifiera att åtgärder och reaktionskrafter inte är ogiltiga och kan ge rörelser.

Två åkare på isen eller på en mycket slät yta kan drivas var och en.

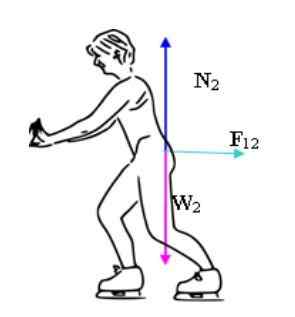
Tänk på två åkare med helt annan deg. De är mitt i en ishall med föraktlig friktion och är initialt i vila. I ett givet ögonblick skjuter de varandra och applicerar konstant styrka med handflatorna. Hur kommer båda att röra sig?

Kan tjäna dig: Balanseringsvektor: Beräkning, exempel, övningarTvå åkare drivs i mitten av en isbana. Källa: Benjamin Crowell (Wikipedia-användare BCROWELL) [CC BY-SA 3.0 (http: // Creativecommons.Org/licenser/BY-SA/3.0/]]

Det är viktigt att betona att eftersom det är en yta utan friktion är de enda obalanserade krafterna de krafter som åkare tillämpar varandra. Medan vikten och normal agerar på båda, är dessa krafter balanserade, från vad åkarna skulle accelerera i vertikal riktning.

Formler tillämpas i detta exempel

Newtons tredje lag säger att:

F₁₂ = -F_tjugoett

Det vill säga kraften som utövas av skater 1 på 2, är densamma i storlek som de två utövar på 1, med samma riktning och motsatt riktning. Observera att dessa krafter tillämpas på olika föremål, på samma sätt som krafterna var på bollen och jorden i det föregående konceptuella exemplet.

m₁ till₁ = -m₂ till₂

Eftersom krafterna är motsatta kommer de accelerationer som orsakar också att vara, men deras storlekar kommer att vara annorlunda, eftersom varje skater har en annan massa. Låt oss titta på den acceleration som förvärvats av den första åkare:

Om massan på den första skateren är större än den andra kommer dess acceleration att vara lägre. Detta kan förväntas eftersom det har en större tröghet. Den lättaste skateren får större acceleration. Om massorna är desamma kommer accelerationerna också att vara.

Så rörelsen som händer nedan är separationen av båda åkare i motsatta sinnen. I princip var åkarna i vila mitt i banan. Var och en utövar en kraft på den andra som ger en acceleration medan händerna är i kontakt och drivkraften varar.

Efter det rör sig åkarna bort från varandra med enhetlig rätlinjig rörelse, genom att inte agera obalanserade krafter. Hastigheten på varje skridskoåkare kommer att vara annorlunda om deras massor också är.

Träning löst

För att lösa problem där Newtons lagar måste tillämpas är det nödvändigt att noggrant rita de krafter som verkar på objektet. Denna ritning kallas "Free Body Diagram" eller "Isolated Body Diagram". I detta diagram bör de krafter som kroppen utövar på andra objekt inte visas.

Om det finns mer än ett objekt som är involverat i problemet är det nödvändigt.

1- Skatarna från föregående avsnitt har respektive massor m₁ = 50 kg och m₂ = 80 kg. De skjuter varandra med en konstant kraft på 200 n. Drivkraften har en varaktighet på 0.40 sekunder. Hitta:

a) Accelerationen som förvärvats av varje skater tack vare drivkraften.

b) hastigheten för var och en när de separerar

Lösning

a) Ta som en horisontell positiv adress den som går från vänster till höger. Att tillämpa Newtons andra lag med de värden som tillhandahålls av uttalandet är:

F_tjugoett = m₁till₁

Varifrån:

För den andra åkare:

b) För att beräkna hastigheten som de bär just när de är separata används de kinematiska ekvationerna för den jämnt accelererade rätlinjiga rörelsen:

Kan tjäna dig: ömsesidig induktans: formel/koefficient, applikationer, övningar

Den initiala hastigheten är 0, eftersom de var i vila mitt i banan:

v_F = Vid

v_F1 = a₁t = -4 m/s² . 0.40 s = -1.6 m/s

v_F2 = a₂T = +2.5 m/s² . 0.40 s = +1 m/s

Resultat

Som förväntat får person 1 lättare större acceleration och därför snabbare hastighet. Observera nu följande om produkten från degen på grund av hastigheten på varje skridskoåkare:

m₁ v₁ = 50 kg . (-1.6 m/s) = - 80 kg.Fröken

m₂ v₂ = 80 kg . 1 m/s = +80 kg.Fröken

Summan av båda produkterna är 0. Produkten av massan med hastighet kallas mängden rörelse P. Det är en vektor med samma riktning och känsla av hastighet. När åkarna var i vila och händerna i kontakt, kunde det antas att de bildade samma objekt vars rörelse var:

P_antingen = (m₁ +m₂v_antingen = 0

När drivkraften är klar förblir rörelsens rörelse 0. Därför bevaras mängden rörelse.

Exempel på Newtons tredje lag i vardagen

Gå

Walking är en av de mest dagliga åtgärder som kan genomföras. Om den noggrant observeras kräver gångåtgärderna att du skjuter foten mot marken, så att den returnerar en lika och motsatt kraft på foten av vandraren.

När vi ständigt tillämpade Newtons tredje lag. Källa: Pixabay.

Det är just den kraften som gör att människor kan gå. På flygningen utövar fåglarna styrka i luften och luften skjuter vingarna så att fågeln drivs framåt.

Bilrörelse

I en bil utövar hjulen styrka på trottoaren. Tack vare trottoarreaktionen utövar den på däckkrafterna som driver bilen framåt.

Sport

I idrottspraxis är handlings- och reaktionskrafterna många och har ett mycket aktivt deltagande.

Låt oss till exempel se idrottaren med foten som stöds av ett startblock. Blocket ger en normal kraft som en reaktion på den drivkraft som idrottaren utövar på det. Resultatet av denna normala och vikten av korridoren resulterar i en horisontell kraft som gör att idrottaren kan köra framåt.

Idrottaren använder startblocket för att lägga till impuls framåt vid utgången. Källa: Pixabay.

Brandslangar

Ett annat exempel där Newtons tredje lag finns finns i brandmän som håller eldslangar. Slutet på dessa stora slangar har ett handtag på munstycket som brandmannen måste hålla när vattenstrålen kommer ut, för att undvika bakslaget som uppstår när vattnet kommer ut i full fart.

Av samma anledning är det bekvämt.

Referenser

1. Giancoli, D.  2006. Fysik: Principer med applikationer. Sjätte upplagan. Prentice hall. 80 - 82.
2. Rex, a. 2011. Fysikens grunder. Pearson. 73 - 75.
3. Tipler, s. 2010. Fysisk. Volym 1. Femte upplagan. Redaktör. 94 - 95.
4. Akter, D. 2002. Astronomer för astronaver. Taget från: pwg.Gsfc.pott.Gov.