Typer av vinklar, egenskaper och exempel

Det finns olika Typer av vinklar, Med hänsyn till flera kriterier för att differentiera dem, till exempel kan de särskiljas genom sin mått, genom den position de upptar och även enligt summan med andra vinklar.

Vanligtvis definieras en vinkel som öppningen mellan två semi -rakt med ett gemensamt ursprung, kallad vertex av vinkeln. De amplitud Öppning är måtten på vinkeln, som ofta kommer i grader eller radianer.

En examen motsvarar en av de 360 ​​delarna där en omkrets kan delas. Om omkretsen är uppdelad i två lika delar, är var och en lika med 180 grader eller 180º, om den istället är uppdelad i fyra lika delar, kommer var och en att vara 90º och så vidare. Detta system kallas Sexagesimal.

Radianes är en annan mycket använt mått, som består av att ta en omkrets och mäta vinkeln mellan två av dess radioapparater, vars längd är "R" och med toppen i mitten av omkretsen. På detta sätt påstås också bågen "S" mellan dessa radioapparater "R" och vinkeln är underlags och är 1 radián eller 1 rad och är lika med 57.3: e graden.

Instrumentet för att mäta vinklar är transportören. För att vidta ett mått sammanfaller transportörens centrum med vinkelns toppunkt och en av sidorna på densamma med transportörens 0º -linje. Den andra sidan sammanfaller med måtten på vinkeln, som läses på skalan.

Typer av vinklar enligt ditt mått

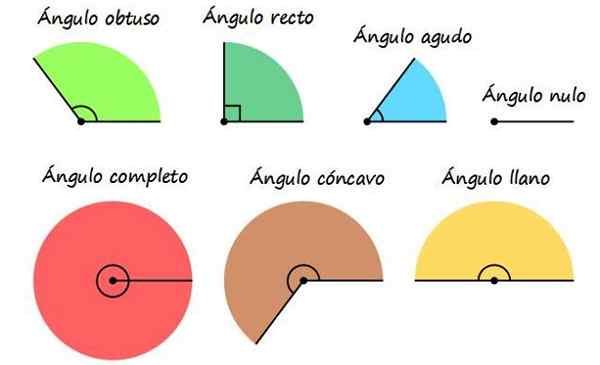
Klassificering av vinklar genom deras mått. Källa: Wikimedia Commons.

Ett av de vanligaste sätten att hänvisa till vinklar är att namnge dem enligt deras mått, även om en vinkel ibland kan tillhöra mer än en kategori av beskrivet nedan.

Kan tjäna dig: Variationskoefficient: Vad är det för, beräkning, exempel, övningar

Nollvinkel

Den vars åtgärd är 0º eller 0 rad, det vill säga de två halvtakten har en nollöppning.

Spetsig vinkel

Måttet på en akut vinkel är mellan 0 och 90º eller mellan 0 och π/2 radianer. Till exempel är vinklar på 30 °, 45º och 60º, som är en del av de anmärkningsvärda vinklarna, alla akuta vinklar.

Rätt vinkel

Det är den som mäter exakt 90º (π/2 radianer), detta betyder att de halvstammar som definierar den är vinkelrätt mot varandra.  De inre vinklarna på en fyrkant eller en rektangel är raka vinklar, och det är också en rak vinkel som bildas mellan kateterna i en rektangel triangel.

Trubbig vinkel

Det är en vinkel som är större än 90º eller π/2 radianer.

Platt vinkel

Den mäter exakt 180º, motsvarande π -radianer. När en vektoriell storlek är motsatt till en annan bildar de en vinkel på 180º, till exempel hastigheten på en mobil som rör sig i en rak linje och retardationen upplevs när den stoppas.

Konvex vinkel

När en vinkel mäter mindre än 180º är en konvex vinkel. En akut vinkel kan vara konvex, som en av 90º och de stöt vinklar vars mått ingår i 90º och 180º. Fler exempel på konvexa vinklar är:

• 45º
• 60º
• 75º
• 135º

Konkav vinkel

Det är den som mäter mer än 180º, såsom 225º eller 270º, den senare är lika med tre fjärdedelar av omkretsen.

Full eller perigonal vinkel

Måttet är 360 ° eller 2π -radianer. Det betyder att de två halvstammarna som gör det sammanfaller igen, men till skillnad från nollvinkeln, i detta fall har det varit en fullständig vändning.

Kan tjäna dig: oval (geometrisk figur): egenskaper, exempel, övningar

Typer av vinklar enligt deras sidor

I många figurer och geometriska strukturer visas mer än en vinkel och det är därför det är bekvämt att ha ett kriterium för att jämföra sidorna på en med avseende på en annan. På detta sätt har de:

På varandra följande vinklar

De på varandra följande vinklarna ligger bredvid varandra, därför har de en gemensam sida och toppunkt.

Angränsande vinklar

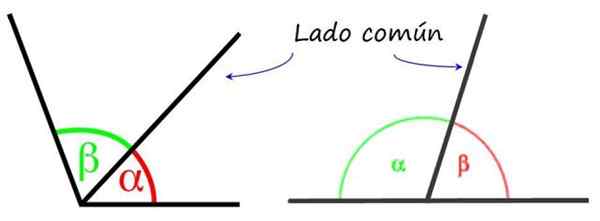På vänster två på varandra följande vinklar och till höger två angränsande vinklar. Källa: Wikimedia Commons/F. Zapata.

De angränsande vinklarna har en gemensam sida och toppunkt, det vill säga de presenterar sig bredvid den andra. Men till skillnad från de på varandra följande vinklarna, i de angränsande vinklarna är de återstående sidorna motsatta semi -tight, därför mellan de två vinklarna totalt 180º.

Motsatta vinklar av toppunkten

De motsatta vinklarna i toppen har toppunktet gemensamt, och deras sidor sträcker sig motsatt, från en av vinklarna till den andra. På detta sätt har de motsatta vinklarna från toppunkten samma mått.

Följande figur visar 4 vinklar, betecknade med grekiska bokstäver. De blå vinklarna är a och p, och som framgår är de akuta och motsatta vinklar av toppunkten. Å andra sidan är vinklarna γ och Δ stöt vinklar och motsätter sig också av toppunkten.

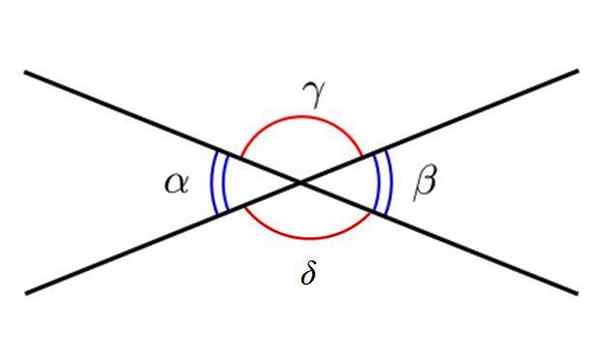Motsatta vinklar av toppunkten. Källa: Wikimedia Commons.

Typer av vinklar enligt summan av deras mått

Vissa beräkningar, särskilt i trigonometri, är mycket förenklade genom att observera om summan av måtten på två vinklar är den för en av de anmärkningsvärda vinklarna, såsom rätt vinkel (90º) eller den plana vinkeln (180º). Enligt detta har de:

Kompletterande vinklar

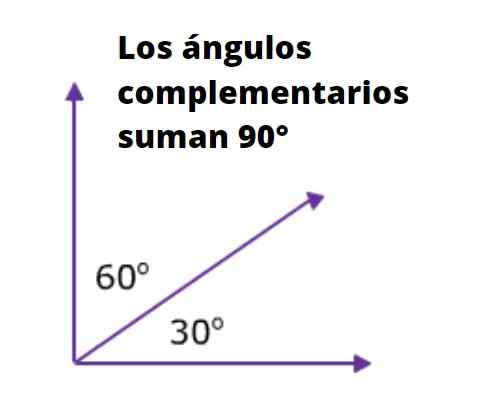
De vinklar vars summa är lika med 90º är komplementära. Till exempel är de inre akuta vinklarna i en rektangel triangel komplementär, eftersom summan av dess tre inre vinklar är lika med 180º.

Kan tjäna dig: 90 delare: vad är och förklaring

Eftersom en av de inre vinklarna i rektangeln mäter 90º är summan av de andra två också lika med 90º.

Kompletterande vinklar

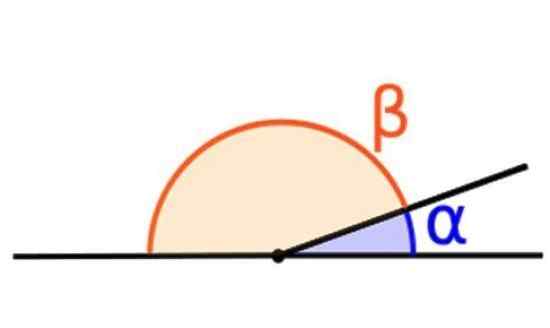Summan av två kompletterande vinklar är lika med 180º. Källa: Wikimedia Commons.

Är de vinklar vars summa är lika med 180º. Till exempel vinklarna a och ß som visas i den övre figuren.

Exempel på anmärkningsvärda vinklar som samtidigt är kompletterande är:

• 120º och 60º
• 135º och 45º

Referenser

1. Alexander, D. 2013. Geometri. Femte. Utgåva. Cengage Learning.
2. Baldor. 1983. Flat och rymd- och trigonometri -geometri. Kulturhem.
3. OCH. TILL. 2003. Geometrielement: med övningar och kompassgeometri. University of Medellin.
4. Geometri 1st. Vinklar i omkretsen. Återhämtat sig från: edu.Xunta.är.
5. Rik, b. Geometri. 1991. Schaumserie. 2: a. Utgåva. McGraw Hill.