Paraboliska skottegenskaper, formler och ekvationer, exempel

han parabolskott Den består av att kasta ett objekt eller projektil med en viss vinkel och låta den röra sig under tyngdkraften. Om luftmotstånd inte beaktas kommer objektet, oavsett dess natur, att följa en bana i form av en parabola.

Det är en daglig rörelse, eftersom bland de mest populära sporterna är de där bollar eller bollar kastas, antingen för hand, med foten eller med ett instrument som en racket eller en fladdermus till exempel.

Figur 1. Vattenstrålen från prydnadskällan följer en parabolisk bana. Källa: Wikimedia Commons. Zátonyi Sandor (IFJ.), Fizped/CC BY-SA (https: // CreativeCommons.Org/licenser/BY-SA/3.0)

För studie bryts det paraboliska skottet i två överlappande rörelser: en horisontell utan acceleration och det andra vertikala med konstant acceleration ner, vilket är tyngdkraften. Båda rörelserna har initial hastighet.

Låt oss säga att den horisontella rörelsen tar. Var och en av dessa rörelser är oberoende av den andra.

Med tanke på det faktum att bestämma projektilpositionen är de viktigaste målen är det nödvändigt att välja ett lämpligt referenssystem. Detaljerna kommer nästa.

[TOC]

Formler och ekvationer av det paraboliska skottet

Anta att objektet kastas med vinkel a med avseende på den horisontella och initiala hastigheten v_antingen som visas i figuren nedan till vänster. Det paraboliska skottet är en rörelse som äger rum på planet Xy Och i så fall sönderdelas den initiala hastigheten så här:

v_oxe = v_antingen cos a

v_Oy = v_antingen synd

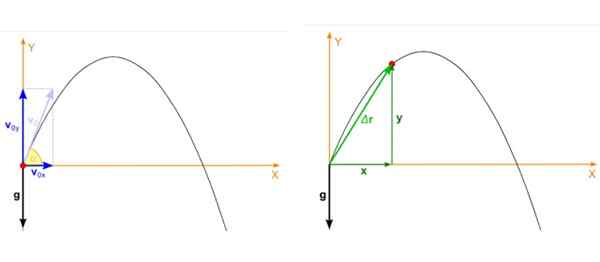figur 2. Till vänster den initiala hastigheten på projektilen och till höger positionen när som helst av lanseringen. Källa: Wikimedia Commons. Zátonyi Sandor, (IFJ.) FIZPED/CC BY-SA (https: // Creativecommons.Org/licenser/BY-SA/3.0).

Projektilpositionen, som är den röda punkten i figur 2, höger bild, har också två komponenter som beror på tid, en i x Och den andra i och. Positionen är en vektor som betecknas som r och dess enheter är av längd.

Kan tjäna dig: isomeria

I figuren sammanfaller projektilens initiala position med ursprunget till koordinatsystemet, därför x_antingen = 0, och_antingen = 0. Detta är inte alltid fallet, ursprunget kan väljas var som helst, men detta val förenklar beräkningarna mycket.

När det gäller de två rörelserna i X och Y, dessa är:

-X (t): Det är en enhetlig rätlinjig rörelse.

-och (t): motsvarar en enhetligt accelererad rätlinjig rörelse med g = 9.8 m/s² och pekar vertikalt ner.

I matematisk form:

x (t) = v_antingen cos a.t

och (t) = v_antingen .synd.T - ½g.t²

Positionvektorn kvarstår:

r (t) = [v_antingen cos a.t]Yo + [v_antingen .synd.T - ½g.t²] J

I dessa ekvationer kommer den uppmärksamma läsaren att märka att minustecknet beror på att svårighetsgraden pekar på marken, den känsla som valts som negativ, medan den är uppåt är den positiv.

Eftersom hastigheten är den första härledda från positionen räcker det att härleda r (t) beträffande tid och erhålla:

v (t) = v_antingen cos a Yo + (v_antingen .synd - Gt) J

Slutligen uttrycks accelerationen vektor som:

till (t) = -g J

- Bana, maximal höjd, maximal tid och horisontell räckvidd

Bana

För att hitta den uttryckliga ekvationen för banan, som är kurvan y (x), måste du eliminera tidsparametern, rensa i ekvationen för x (t) och ersätta i y (t). Förenkling är något mödosam, men det erhålls äntligen:

Maxhöjd

Den maximala höjden inträffar när v_och = 0. Att veta att det finns nästa relation mellan positionen och hastighetens kvadrat:

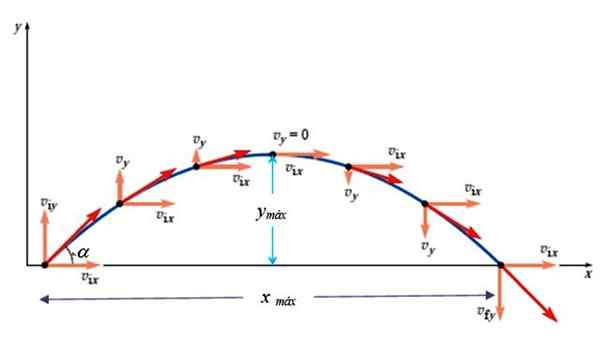Figur 3. Hastigheten i det paraboliska skottet. Källa: Giambattista, a. Fysik.

v_och² = v_Oy ²- 2gy

Gör v_och = 0 Precis när den når med maximal höjd:

0 = v_Oy ²- 2 g.och_max → och_max = v_Oy ²/2 g

Med:

Kan tjäna dig: Centripetal Acceleration: Definition, Formls, Calculation, Ovess

v_Oy = v_antingen senα

Maximal tid

Den maximala tiden är den tid som objektet tar för att nå och_max. För att beräkna det används det:

v_och = v_antingen .synd - Gt

Veta att v_och Det är gjort 0 när t = t_max, resultat:

v_antingen .synd - g.t_max = 0

t_max = v_Oy /g

Maximalt horisontellt intervall och flygtid

Omfånget är mycket viktigt, eftersom det indikerar var objektet kommer att falla. Så vi vet om det ger i vitt eller inte. För att hitta det behöver vi flygtid, total tid eller t_v.

Av den tidigare illustrationen är det lätt att dra slutsatsen att t_v = 2.t_max. Men uppmärksamhet är bara sant om lanseringen är på nivån, det vill säga utgångspunktens höjd är densamma som höjden på ankomsten. Annars är tiden att lösa den andra gradsekvationen som är resultatet av att ersätta den slutliga positionen och_slutlig:

och_slutlig = v_antingen .synd.t_v - ½ g.t_v²

I vilket fall som helst är det maximala horisontella räckvidden:

x_max = v_oxe. t_v

Paraboliska skjutexempel

Det paraboliska skottet är en del av rörelsen hos människor och djur. Också av nästan alla sporter och spel där tyngdkraften ingriper. Till exempel:

Parabolisk skytte i mänskliga aktiviteter

-Stenen som kastas av en katapult.

-Målvaktens målspark.

-Bollen som kastar kannan.

-Pilen som kommer ut ur bågen.

-Alla slags hopp

-Kasta en sten.

-Alla kastvapen.

Figur 4. Stenen som kastas av katapultet och den patey bollen i mållådan är exempel på paraboliska skott. Källa: Wikimedia Commons.

Det paraboliska skottet i naturen

-Vatten som växer från naturliga eller konstgjorda jetflyg som en källa.

-Stenar och lava som spirar från en vulkan.

-En boll som studsar på trottoaren eller en sten som gör det på vattnet.

-Alla slags djur som hoppar: känguruer, delfiner, gaseller, kattdjur, grodor, kaniner eller insekter, för att nämna några.

Det kan tjäna dig: Mekanisk kraft: Vad är, applikationer, exempelFigur 5. Impala kan hoppa upp till 3 m. Källa: Wikimedia Commons. Arturo de Frias Marques/CC BY-S (https: // Creativecommons.Org/licenser/BY-SA/3.0).

Träning

En gräshoppa bildar en vinkel på 55 º med horisontella och landar vid 0.80 meter senare. Hitta:

a) Den maximala höjden nås.

b) Om jag hoppade med samma initiala hastighet, men bildade en vinkel på 45º, skulle den bli högre?

c) Vad kan sägas om den maximala horisontella räckvidden för denna vinkel?

Lösning till

När de uppgifter som tillhandahålls av problemet inte innehåller den initiala hastigheten v_antingen Beräkningarna är något mer mödosamma, men från de kända ekvationerna kan ett nytt uttryck härledas. Med början från:

x_max = v_oxe . t_flyg = v_antingen.cos a. t_v

När den landar senare är höjden 0 igen, sedan:

v_antingen .synd.t_v - ½ g.t_v²= 0

Som t_v Det är en vanlig faktor, det förenklas:

v_antingen .synd - ½ g.t_v= 0

Vi kan rensa T_v Från den första ekvationen:

t_v = x_max / v_antingen.cos a

Och ersätt i den andra:

v_antingen .synd - (½g.x_max / v_antingen.cos a) = 0

Genom att multiplicera alla termer med v_antingen.cos aUttrycket förändras inte och nämnaren försvinner:

(v_antingen .synd.) (v_antingen.cos a) - ½g.x_max = 0

v_antingen² synd. cos a = ½g.x_max

Kan redan rensas v_antingen eller också ersätta följande identitet:

Sen 2α = 2 Sen α. cos a → v_antingen² Sen 2α = g.x_max

Beräknas v_antingen²:

v_antingen² = g.x_max / Sen 2α = (9.8 x 0.8 / sen 110) m²/s² = 8.34 m²/s²

Och slutligen den maximala höjden:

och_max= v_Oy ²/2g = (8.34 x sen² 55)/(2 x 9.8) m = 0.286 m = 28.6 cm

Lösning B

Hummer lyckas bibehålla samma horisontella hastighet, men när vinkeln minskar:

och_max= v_Oy ²/2g = (8.34 x sen² 45)/(2 x 9.8) m = 0.213 m = 21.3 cm

Når en mindre höjd.

Lösning C

Det maximala horisontella räckvidden är:

x_max = v_antingen² Sen 2a / g

När vinkeln varierar förändras också det horisontella räckvidden:

x_max = 8.3. 4 Sen 90 / 9.8  m = 0.851 m = 85.1 cm

Hoppet är längre nu. Läsaren kan verifiera att det är maximalt för vinkeln på 45 º då:

Sin 2α = sin 90 = 1.

Referenser

1. Figueroa, D. 2005. Serie: Physics for Science and Engineering. Volym 1. Kinematik. Redigerad av Douglas Figueroa (USB).
2. Giambattista, a. 2010. Fysik. Andra upplagan. McGraw Hill.
3. Giancoli, D.  2006. Fysik: Principer med applikationer. Sjätte. Ed Prentice Hall.
4. Resnick, r. 1999. Fysisk. Vul. 1. 3: e upplagan. på spanska. Kontinentala redaktionella företag s.TILL. av C.V.
5. Sears, Zemansky. 2016. Universitetsfysik med modern fysik. 14th. Ed. Volym 1.