Isometriska omvandlingar

De isometriska omvandlingar De är förändringar av position eller orientering av en viss figur som inte förändrar formen eller storleken på detta. Dessa transformationer klassificeras i tre typer: översättning, rotation och reflektion (isometri). I allmänhet tillåter geometriska transformationer skapa en ny siffra från en annan given.

En omvandling till en geometrisk figur innebär att den på något sätt utsattes för en viss förändring; det vill säga det ändrades. Enligt känslan av originalet och liknande i planet kan geometriska transformationer klassificeras i tre typer: isometrisk, isomorf och anamorfisk.

Egenskaper för isometriska transformationer

- Isometriska transformationer inträffar när storleken på segmenten och vinklarna mellan den ursprungliga figuren och den transformerade figuren bevaras.

- I denna typ av omvandling ändras inte figurens form eller storlek (de är kongruenta), det är bara en förändring av positionen för detta, antingen i orienteringen eller i den meningen. På detta sätt kommer den ursprungliga siffran och finalen att vara liknande och geometriskt kongruent.

- Isometri hänvisar till jämlikhet; det vill säga att geometriska figurer kommer att vara isometriska om de har samma form och storlek.

- I isometriska transformationer är det enda som kan observeras en förändring av position i planet, en styv rörelse inträffar tack vare vilken figuren går från en första position till en slutlig. Denna figur kallas homolog (liknande) av originalet.

- Det finns tre typer av rörelser som klassificerar en isometrisk omvandling: översättning, rotation och reflektion eller symmetri.

Typer av isometriska transformationer

Genom översättning

Är de isometrier som gör det möjligt att förskjuta i en rak linje alla punkter i planet i en specifik riktning och avstånd.

När en siffra omvandlas genom översättning förändrar den inte sin orientering i förhållande till den ursprungliga positionen, och den förlorar inte heller sina interna mått, måtten på dess vinklar och sidor. Denna typ av förskjutning definieras av tre parametrar:

• En adress som kan vara horisontell, vertikal eller sned.
• En riktning, som kan vara till vänster, höger, upp eller ner.
• Avstånd eller storlek, vilket är den längd som är från den första positionen till finalen i alla punktar som rör sig.

Kan tjäna dig: curtos: definition, typer, formler, vad är det för till exempel

För en isometrisk omvandling på grund av översättning måste den uppfylla följande villkor:

• Figuren måste alltid hålla alla dess dimensioner, både linjära och vinklade.
• Figuren ändrar inte sin position med avseende på den horisontella axeln; det vill säga dess vinkel varierar aldrig.
• Översättningar kommer alltid att sammanfattas i ett, oavsett antalet översättningar.

I ett plan där centret är en punkt eller, med koordinater (0,0), definieras översättningen av en vektor t (a, b), vilket indikerar förskjutningen av den initiala punkten. Det vill säga:

P (x, y) + t (a, b) = p '(x + a, y + b)

Till exempel, om till koordinatpunkten P (8, -2) en översättning T (-4, 7) tillämpas, erhålls det:

P (8, -2) + t (-4, 7) = p '[(8 + (-4)), ((-2) + 7)] = p' (4, 5)

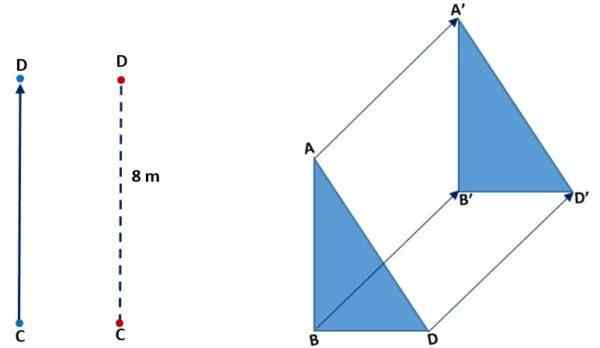
I följande bild (till vänster) kan du se hur punkt C flyttade till sammanfallet med D. Han gjorde det vertikalt, betydelsen gick upp och avståndet eller storleken CD var 8 meter. I rätt bild observeras översättningen av en triangel:

Genom rotation

Är de isometrier som gör att figuren kan vända alla punkter i ett plan. Varje punkt svänger efter en båge som har en konstant vinkel och en fast punkt (vändningscenter) bestämd.

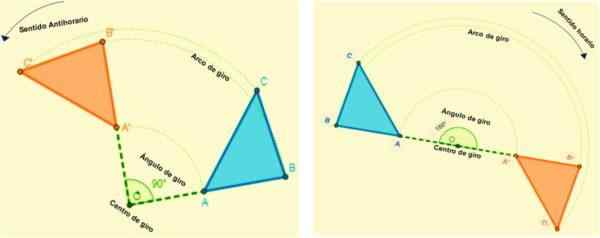
Det vill säga all rotation kommer att definieras av dess rotation och vändningsvinkelcenter. När en figur förvandlas genom rotation upprätthåller den måttet på dess vinklar och sidor.

Rotationen sker i en viss riktning, det är positivt när svängen är anti -horary (i motsats till hur klockan händerna roterar) och negativ när dess tur är i medurs riktning.

Om en punkt (x, y) roteras med avseende på ursprunget -det är, är dess rotationscenter (0,0) -i en vinkel på 90^antingen 360^antingen Koordinaterna för punkterna kommer att vara:

Kan tjäna dig: statistikgrenar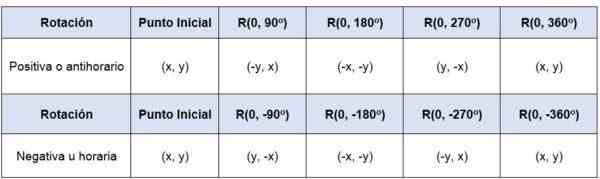

I det fall där rotationen inte har något centrum vid ursprunget måste ursprunget till koordinatsystemet till det nya givna ursprunget överföras för att rotera figuren med ursprung i centrum.

Till exempel, om punkt P (-5,2) en 90-rotation appliceras^antingen, Runt ursprunget och i positiv mening kommer dess nya koordinater att vara (-2,5).

Genom reflektion eller symmetri

Är de omvandlingar som investerar punkterna och siffrorna i planet. Denna investering kan vara med avseende på en punkt eller kan också vara med avseende på en linje.

Med andra ord, i denna typ av transformation är varje punkt i den ursprungliga figuren associerad med en annan punkt (bild) av den homologa figuren, så att punkten och dess bild är på samma avstånd från en linje som kallas symmetriaxel.

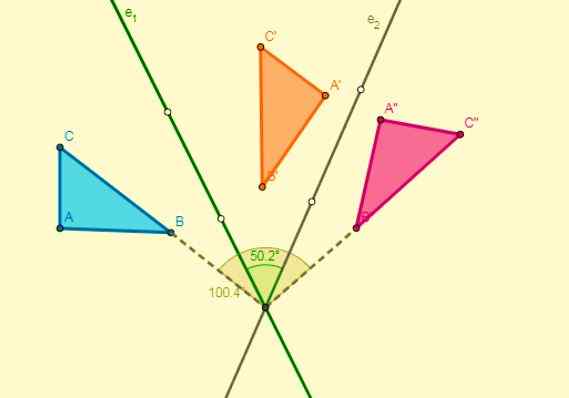
Således kommer den vänstra delen av figuren att återspegla höger sida, utan att ändra formen eller dess dimensioner. Symmetrin förvandlar en lika figur men i omvänd riktning, vilket kan ses i följande bild:

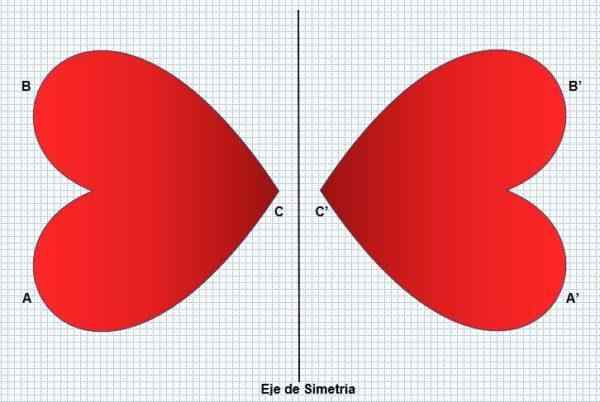
Symmetri finns i många aspekter, till exempel vissa växter (solrosor), djur (påfågel) och naturfenomen (snöflingor). Människan återspeglar det i ansiktet, som anses vara en skönhetsfaktor. Reflektion eller symmetri kan vara av två typer:

Centralsymmetri

Det är den omvandlingen som inträffar med avseende på en punkt, där figuren kan ändra dess orientering. Varje punkt i den ursprungliga figuren och dess bild är på samma avstånd från en punkt eller kallas Symmetry Center. Symmetri är central när:

• Både punkten och dess bild och mitt tillhör samma linje.
• Med en rotation på 180^antingen från mitten eller en figur som är lika med originalet erhålls.
• Slagen av den ursprungliga figuren är parallella med slags slags slag.
• Betydelsen av figuren förändras inte, den kommer alltid att vara i ett schema.

Kan tjäna dig: Hur mycket har du att lägga till 3/4 för att få 6/7?

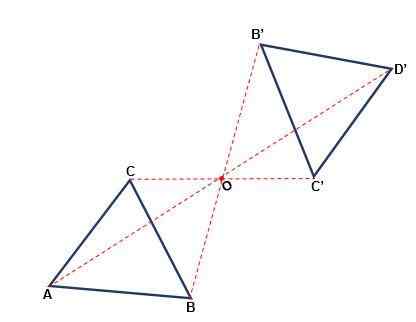Axiell symmetri

Denna omvandling inträffar med avseende på symmetriaxeln, där varje punkt i den initiala figuren är associerad med en annan punkt i bilden och dessa är på samma avstånd som symmetriaxeln. Symmetrin är axiell när:

• Segmentet som går med i en punkt med sin bild är vinkelrätt mot dess symmetriaxel.
• Siffrorna ändrar sin betydelse när det gäller svängen eller tidsriktningen.
• Genom att dela figuren med en central linje (symmetriaxel) sammanfaller en av de resulterande halvorna helt med en annan av halvorna.

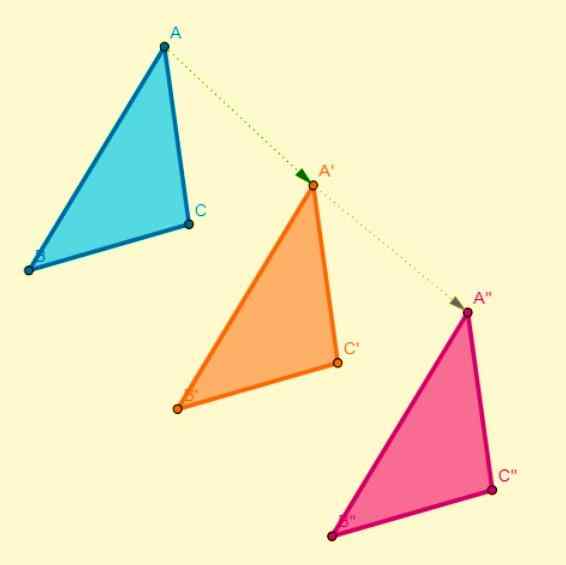
Sammansättning

En isometrisk transformationskomposition hänvisar till den successiva tillämpningen av isometriska transformationer på samma figur.

En översättning

Sammansättningen av två översättningar resulterar i en annan översättning. När den utförs på planet, på den horisontella axeln (x) förblir endast koordinaterna för den axeln, medan koordinaterna för den vertikala axeln (y) förblir desamma och vice versa.

Rotationens sammansättning

Sammansättningen av två varv med samma centrum resulterar i en annan sväng, som har samma centrum och vars amplitud kommer att vara summan av amplituderna för de två varvarna.

Om centrum svängarna har olika centrum kommer snittet av de två segmenten av liknande punkter att vara rotationens centrum.

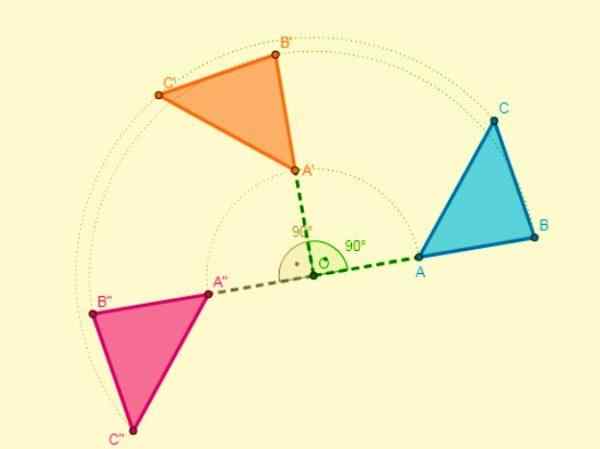
Symmetri sammansättning

I detta fall beror kompositionen på hur den tillämpas:

• Om samma symmetri tillämpas två gånger kommer resultatet att vara en identitet.
• Om två symmetrier appliceras med avseende på två parallella axlar kommer resultatet att vara översättning, och deras förskjutning är dubbelt så mycket som dessa axlar:

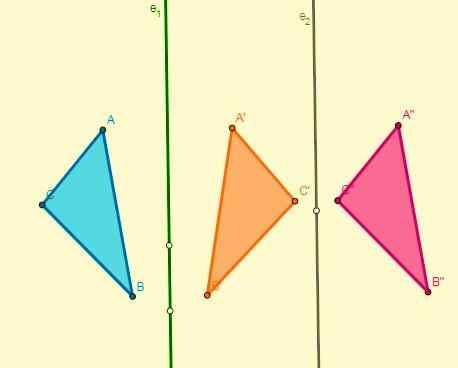
• Om två symmetrier appliceras med avseende på två axlar som skärs vid punkt O (mitt), kommer en rotation med mitten att erhållas och dess vinkel kommer att vara dubbelt den vinkel som axlarna bildas: