Laplace Transform
- 4786
- 1274
- Hans Olsson
Vad är Laplace's Transform?
De Laplace Transform Det har varit under de senaste åren av stor betydelse inom teknik, matematik, fysik, bland andra vetenskapliga områden, eftersom det förutom att de är av stort intresse för det teoretiska, ger ett enkelt sätt att lösa differentiella ekvationer och förvandla dem till algebraiska ekvationer.
Ursprungligen presenterades Laplace-transformen av Pierre-Simon Laplace (1745-1827) i sin studie om teorin om sannolikhet, och i princip behandlades som ett matematiskt objekt med bara teoretiskt intresse.
Aktuella tillämpningar uppstår när olika matematiker försökte ge en formell motivering till de "operativa reglerna" som Oliver Heaviside använde (1850-1925) i studien av ekvationer av elektromagnetisk teori.
Definition av Laplace Transform
Låt f vara en definierad funktion för t ≥ 0. Laplace -transform definieras enligt följande:
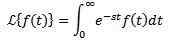
Det sägs att Laplace -transformen finns om de tidigare integrerade konvergerna, annars sägs det att Laplace -transformen inte finns.
I allmänhet, för att beteckna den funktion som önskas för att omvandla små bokstäver och kapitalbrevet motsvarar dess transformation. På detta sätt kommer vi att ha:
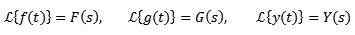
Exempel
Tänk på konstant funktion f (t) = 1. Vi måste förvandla:
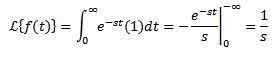
Under förutsättning att de integrerade konvergerar, det vill säga förutsatt att s> 0. Annars s < 0, la integral diverge.
Låt g (t) = t. Hans Laplace -transformation ges av:
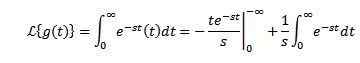
När du integreras av delar och vet det-St Det tenderar till 0 när t tenderar att oändliga och s> 0, tillsammans med föregående exempel måste vi:
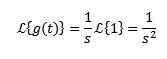
Det transformala kan eller inte finns, till exempel för funktionen f (t) = 1/t, den integrerade som definierar dess laplace -transform konvergerar inte och därför finns dess transformerade inte.
De tillräckliga förhållandena för att säkerställa att Laplace -omvandlingen av en funktion f finns, är att f är kontinuerlig i delar för t ≥ 0 och är av exponentiell ordning.
Det sägs att en funktion är kontinuerlig i delar för t ≥ 0, när det för något intervall [a, b] med a> 0 finns ett ändligt antal punkter tk, Där f har diskontinuiteter och är kontinuerlig i varje underinterval [tK-1,tk].
Å andra sidan sägs det att en exponentiell funktion C om det finns verkliga konstanter M> 0, C och T> 0 så att:
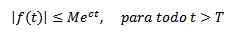
Som exempel måste vi f (t) = t2 Det är exponentiellt, eftersom | t2| < e3t För alla t> 0.
Formellt har vi följande sats:
Sats (tillräckliga villkor för existens)
Om f är en kontinuerlig funktion för t> 0 och exponentiell c, finns det Laplace -transformen för s> c.
Det är viktigt att lyfta fram att detta är ett tillstånd av tillräcklighet, det vill säga att det kan finnas ett fall att det finns en funktion som inte uppfyller dessa förhållanden och ändå finns dess laplace -transform finns.
Ett exempel på detta är funktionen f (t) = t-1/2 vilket inte är kontinuerligt i delar för t ≥ 0 men dess laplace -transform finns.
Laplace -omvandling av vissa grundläggande funktioner
Följande tabell visar Laplace -omvandlingarna av de vanligaste funktionerna.
Kan tjäna dig: hela siffror
Historien om Laplace -transformen
Laplace-transformen är skyldig sitt namn till Pierre-Simon Laplace, matematiker och fransk astronom och teoretiker som föddes 1749 och dog 1827. Hans berömmelse var sådan att han var känd som Newton i Frankrike.
1744 ägnade Leonard Euler (1707-1783) sina studier till integraler med formen
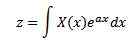
som lösningar av vanliga differentiella ekvationer, men övergav snabbt denna forskning. Senare undersökte Joseph Louis Lagrange (1736-1813), som beundrade Euler mycket, denna typ av integral och relaterade dem till teorin om sannolikhet.
1782, Laplace
1782 började Laplace studera dessa integraler som lösningar på differentiella ekvationer och enligt historiker beslutade han 1785 att omformulera problemet, som senare födde Laplace's omvandlingar som de förstås idag.
Efter att ha introducerats inom området sannolikhetsteori var det av lite intresse för ögonblickens forskare och sågs bara som ett matematiskt objekt endast av teoretiskt intresse.
Heaviside Oliver
Det var i mitten av nittonhundratalet när den engelska ingenjören Oliver Heaviside upptäckte att differentiella operatörer kan behandlas som algebraiska variabler och därmed gav deras moderna tillämpning till Laplace -omvandlingar.
Oliver Heaviside var fysiker, engelska elektriska och matematiska ingenjörer som föddes 1850 i London och dog 1925. Medan man försökte lösa problem med differentiella ekvationer som tillämpades på vibrationsteori och med hjälp av Laplace -studier började det forma de moderna tillämpningarna av Lapla Transforms.
Resultaten exponerade av Heaviside sprids snabbt.
Användbarheten av Heavisides arbete vid lösning av fysikekvationer fick emellertid att deras metoder var populära mellan fysiker och ingenjörer.
Trots dessa bakslag och efter några decennier av misslyckade försök kunde det i början av 1900 -talet ges en rigorös motivering till de operativa reglerna som fastställts av Heaviside.
Dessa försök lönade sig tack vare ansträngningarna från olika matematiker, som Bromwich, Carson, van der Pol, bland andra.
Laplace transformerar egenskaper
Bland egenskaperna för Laplace -transformen sticker ut: Följande sticker ut:
Linearitet
Låt C1 och C2 konstant och f (t) och g (t) funktioner vars omvandlingar av laplace är f (s) respektive g (s), då måste det:
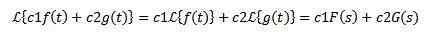
På grund av den här egenskapen sägs det att Laplace Transform är en linjär operatör.
Exempel:
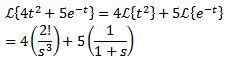
Första översättningen teorem
Om det händer det:
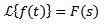
Och 'a' är något riktigt nummer, då:
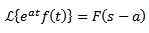
Exempel:
Som Laplace de cos transform (2t) = S/(S^2 + 4) då:
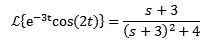
Andra översättningen teorem
Ja
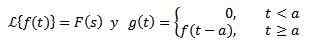
Så
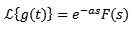
Exempel:
Om f (t) = t^3, då f (s) = 6/s^4. Och därför omvandlingen av
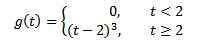
är g (s) = 6e-2s/s^4
Skalaförändring
Ja
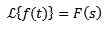
Och 'a' är ett riktigt annorlunda än noll, vi måste
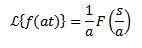
Exempel:
Eftersom transformationen av f (t) = sen (t) är f (s) = 1/(s^2 + 1)
Kan tjäna dig: utvecklad notation: vad är, exempel och övningar
Laplace förvandlades från derivat
Om f, f ', f ", ..., f(N) De är kontinuerliga för t ≥ 0 och är exponentiella och f(N)(t) är kontinuerligt i delar för t ≥ 0, då
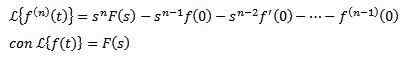
Integral Laplace Transform
Ja
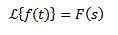
Så
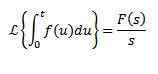
Multiplikation av Tn
Om vi måste
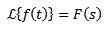
Så
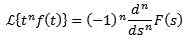
Division av T
Om vi måste
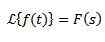
Så
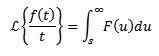
Periodiska funktioner
Låt f vara en periodisk funktion med period t> 0, det vill säga f (t +t) = f (t), sedan
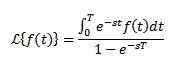
Beteende hos f (s) när s tenderar att oändliga
Om F är kontinuerligt i delar och av exponentiell ordning och
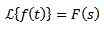
Så
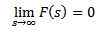
Omvänd förvandlad
När vi applicerar Laplace -transformen till en funktion f (t) får vi f (s), som representerar sagt transform. På samma sätt kan vi säga att f (t) är omvandlingen av den omvända laplace av f (s) och är skriven som
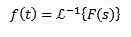
Vi vet att Laplace -omvandlingarna av f (t) = 1 och g (t) = t är f (s) = 1/s och g (s) = 1/s2 Därför måste vi därför

Vissa vanliga Laplace -omvandlade är följande

Dessutom är den omvända Laplace -transformen linjär, det vill säga det uppfylls det
Träning
Hitta
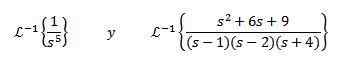
För att lösa denna övning måste vi matcha f (s) -funktionen med några av de föregående tabellen. I det här fallet, om vi tar N + 1 = 5 och använder den omvända transformationens linearitetsegenskap, multiplicerar vi och delar med 4! Komma
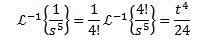
För den andra omvända transformen tillämpar vi partiella fraktioner för att skriva om funktionen F (er) och sedan egenskapen för lineariteten och erhålla

Som vi kan se från dessa exempel är det vanligt att funktionen F (er) som utvärderas inte matchar exakt någon av de funktioner som anges i tabellen. För dessa fall, som observerats, räcker det för att skriva om funktionen tills den når rätt form.
Laplace Transform -applikationer
Differentiella ekvationer
Den huvudsakliga applikationen som Laplace Transforms har är att lösa differentiella ekvationer.
Att använda egenskapen för transformation av ett derivat är det uppenbart att
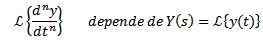
Och av N-1-härledda utvärderade vid t = 0.
Den här egenskapen gör den transformerade.
Följande exempel visar hur man använder Laplace -transformen för att lösa differentiella ekvationer.
Exempel 1
Med tanke på följande initialvärdeproblem
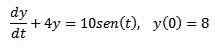
Använd Laplace -transformen för att hitta lösningen.
Vi tillämpar Laplace -transformen på varje medlem av differentiell ekvation
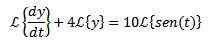
För egenskapen av omvandlingen av ett derivat vi har
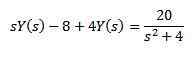
När vi utvecklar allt uttryck och rensning och (er) har vi
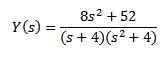
Använda partiella fraktioner för att skriva om höger sida av ekvationen vi får
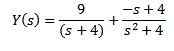
Slutligen är vårt mål att hitta en funktion och (t) som uppfyller differentiell ekvation. Att använda den omvända Laplace -omvandlingen resulterar i
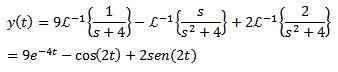
Exempel 2
Lösa
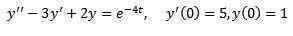
Liksom i föregående fall tillämpar vi transformerade på båda sidor av ekvationen och separat terminer.
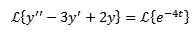
På detta sätt har vi som ett resultat
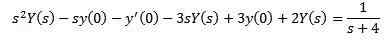
Ersätter med de initiala värdena som ges och rensning och (er)
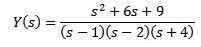
Med hjälp av enkla fraktioner kan vi skriva om hur ekvationen följer
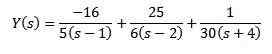
Och tillämpning av omvänd transformation av Laplace ger oss som ett resultat

I dessa exempel kan fel slutsats nås att denna metod inte är mycket bättre än traditionella metoder för att lösa differentiella ekvationer.
Kan tjäna dig: proportionFördelarna som erbjuds av Laplace -transformationen är att den inte är nödvändig.
Dessutom, när vi löser initialvärdeproblem med denna metod, från början använder vi de initiala förhållandena, så det är inte nödvändigt att utföra andra beräkningar för att hitta den specifika lösningen.
Differentiella ekvationer
Laplace -transform kan också användas för att hitta lösningar på samtidiga vanliga differentiella ekvationer, som visas i följande exempel.
Exempel
Lösa
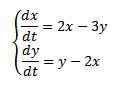
Med de initiala förhållandena x (0) = 8 e y (0) = 3.
Om vi måste
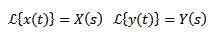
Så
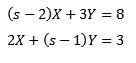
Lösning ger oss som ett resultat
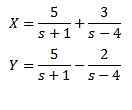
Och när vi applicerar omvänd transformation av Laplace har vi
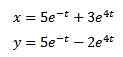
Mekanik och elektriska kretsar
Laplace Transform är av stor betydelse i fysik, har främst applikationer för mekanik och elektriska kretsar.
En enkel elektrisk krets består av följande element:
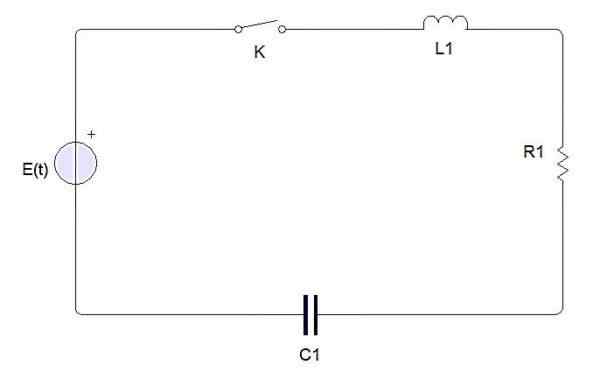 Element i en elektrisk krets
Element i en elektrisk krets En switch, ett batteri eller källa, en induktor, ett motstånd och en kondensator. När omkopplaren är stängd en elektrisk ström som betecknas av i (t). Kondensatorbelastningen betecknas med Q (t).
Genom Kirchhoffs andra lag måste den spänning som produceras av Fuente E till den stängda kretsen vara lika med summan av var och en av spänningsfallen.
Elektrisk ström I (t) är relaterad till belastning q (t) i kondensatorn genom i = dq/dt. Å andra sidan definieras spänningsfallet i vart och ett av elementen på följande sätt:
Spänningsfallet i ett motstånd är ir = r (dq/dt)
Spänningsfallet i en induktor är l (di/dt) = l (d2Q/DT2)
Spänningsfallet i en kondensator är Q/C
Med dessa data och tillämpning av Kirchhoffs andra lag på den enkla enkla kretsen erhålls en andra ordningens differentiella ekvation som beskriver systemet och gör att vi kan bestämma värdet på Q (t).
Exempel
En induktor, en kondensator och motstånd är anslutna till ett batteri E, som visas i figuren. Induktorn är 2 Henries, 0,02 Farads kondensator och 16 Onhmios -motståndet. För tillfället stänger t = 0 kretsen. Hitta lasten och strömmen när som helst t> 0 om E = 300 volt.
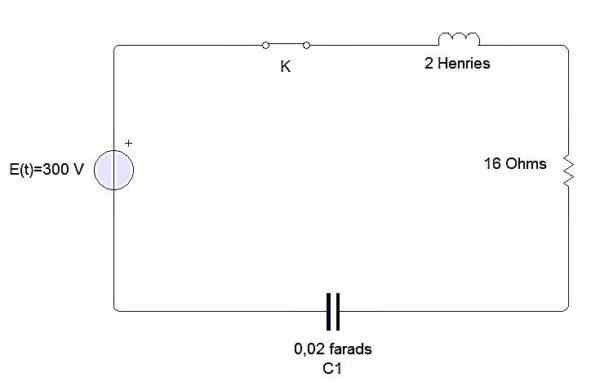
Vi har att den differentiella ekvationen som beskriver denna krets är som följer:
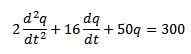
Där de initiala förhållandena är q (0) = 0, i (0) = 0 = q '(0).
Tillämpa Laplace -transformen får vi det
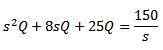
Och rensa q (t)
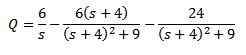
Sedan tillämpa den omvända Laplace -transformationen vi har
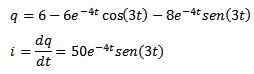
Referenser
- G.Holbrook, J. (1987). Laplace Transform för elektronikingenjörer. Limusa.
- Ruiz, L. M., & Hernandez, m. P. (2006). Differentiella och transformerade ekvationer av Laplace med applikationer. UPV -redaktion.
- Simmons, g. F. (1993). Differentiella ekvationer med historiska tillämpningar och anteckningar. McGraw-hill.
- Spiegel, m. R. (1991). Laplace transformerad. McGraw-hill.
- Zill, D. G., & Cullen, M. R. (2008). Differentiella ekvationer med värden på värdepapper i gränsen. Cengage Learning Editores, s.TILL.

