Tidmästare

Figur 1.- Till vänster en regelbunden Tridecácácone och till höger en valuta på 20 kronor i Tjeckien, med en Bridecagon -formad kontur inskriven i en omkrets, å ena sidan har den lejon av Böhmen och å andra sidan San Wenceslao, beskyddare av Tjeckien, monterad på hästryggen. Källa: f. Zapata.

Vad är en tridecágono?

Tridecagon är en platt geometrisk figur av familjen Polygons och som kännetecknas av att ha 13 sidor och 13 vertikaler. Ett annat namn för denna polygon är Triskaidecágono, Antal härrörande från grekiska.

De 13 sidorna är linjesegment som äntligen är nära att forma figuren. Polygonerna, som heter enligt mängden sidor, är en rik inspirationskälla för arkitektur, konstruktion och design av många föremål, både konst och utilitarier.

Tridecágono

Tridecágono delar med de andra polygonerna följande egenskaper och egenskaper:

-Sidor, De är linjesegmenten som förenas för att bilda figuren, som i fallet med Tridecágono är 13. De identifieras med små bokstäver.

-Häckar, Detta är vad skärningspunkterna på på varandra följande sidor kallas och anger vanligtvis med stora bokstäver. Tridecágono har 13 vertikaler.

-Omkrets, motsvarande summan av sidorna. Om alla sidor har lika mått "A" är omkretsen helt enkelt 13 × A, men om sidorna är ojämlika, lägger omkretsen till var och en av sidorna på sidorna.

-Centrum, Det är poängen som håller samma avstånd med både topparna och sidorna.

-Diagonal, En linje som förenar ett toppunkt till en annan icke -konsekutiv vertex (de på varandra följande topparna är förenade av sidorna).

-Inre vinklar, De bildas mellan två angränsande sidor av figuren och på den inre delen av polygonen, och dess toppunkt är det vanliga toppunktet för båda sidor.

Kan tjäna dig: Miletus sådan teorem

-Yttre vinklar, De är utanför polygonen, mellan ena sidan och förlängningen av en av de på varandra följande sidorna till den första.

-Radio, Distansavstånd-vertix av Tridecágon.

-Centralvinkel, Det är den vars toppunkt är centrum för polygonen.

-Apotem, segment som går med i mitten av en sida med figurens centrum och form 90º med den sidan.

Regelbunden och oregelbunden åska

Treecarons kan vara:

-Regelbunden, När måttet på alla dess tretton sidor är densamma och dess inre vinklar mäter samma.

-Oregelbunden, Om en eller flera av sidorna har olika åtgärder.

När det gäller den vanliga Tridecácágasonen kan följande formler tillämpas:

Inre vinkel

För en vanlig polygon är formeln som gör det möjligt att beräkna värdet på den inre vinkeln:

Där n representerar antalet sidor, som i detta fall är 13. Med detta värde är det:

I = (11 × 180º)/13 ≈ 152.3: e

Diagonaler

Antalet diagonaler beräknas med följande formel, till och med giltigt om polygonen är oregelbunden:

För n = 13 resultat:

D = 13 × 10/2 = 65 diagonaler

Apotem

Värdet på apotem l_TILL  Det beräknas med följande formel, som är "en" sidans längd:

L_TILL ≅ 2.0286A

Område

Om omkretsen p och längden på apotem l_TILL, Tridecágono -området beräknas av:

A = (p × l_TILL)/2

Beroende på "A" -sidan kvarstår formeln:

A = (13a × l_TILL)/2

Ersätta åtgärden_TILL Från föregående avsnitt erhålls en formel för det område som bara beror på sidans längd:

A = (13a × 2.0286a)/2 ≈ 13.186a²

Kan tjäna dig: hypergeometrisk distribution: formler, ekvationer, modell

Träning

Om diametern på en 20 mm kron är 26 mm, hur mycket är sidan och området på Tridecágono registrerat i valutas cirkel?

Lösning

Från figuren finns en rektangel triangel, vars kategorier är apotemet och hälften av sidans längd, med hypotenusa lika med valutas radie, som är hälften av diametern. Eftersom detta är värt 26 mm är Radio R lika med 13 mm.

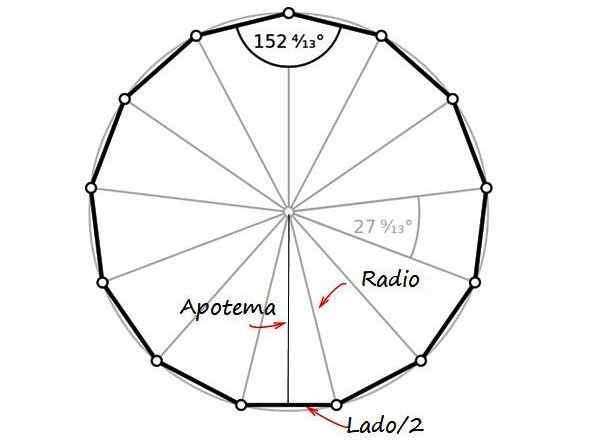figur 2. Radion, apotemen och hälften av sidan av trindecagon bildar en rektangel triangel. Källa: Wikimedia Commons/F. Zapata.

Av Pythagoras teorem:

Sedan L_TILL ≈ 2.0286a, du har:

R² = (2.0286a)² + (0.5: e)² = 4.3652a²

Sidan är:

Med detta värde är valutans område:

A ≈ 13.186a² = 13.186 (6.222mm)² = 510.5 mm²

Läsaren lämnas för att jämföra detta resultat med det område som erhålls genom att anta att valutan är cirkulär i radie r = 13 mm.

Hur är en tridecágono?

Den vanliga trindecagon är av polygonerna som inte medger exakt konstruktion med endast regel och kompass, det vill säga det är inte en byggbar polygon. De är bara byggbara, åtminstone i teorin, de polygoner vars antal sidor endast innehåller främsta faktorer i formen:

Prime -siffrorna på det sättet kallas Fermatkusiner, Men numret 13, även om det är kusin, har inte denna form.

Du kan dock rita en regelbunden trindecagon som är registrerad i en omkrets, varje toppunkt har skärningspunkten med den, utan att bli märkt i blotta ögat. För detta är det nödvändigt.

Kan tjäna dig: obtusangle triangel

Ett sätt att bygga en regelbunden Tridecácágason, även om det inte är den enda, är att dra slagen som visas i följande animation:

Figur 3. Konstruktion av en vanlig tridekagon. Källa: Wikimedia Commons.

Och denna andra animation beskriver också hur man gör en Tridecágono ungefär, med regel och kompass:

Figur 4.- Alternativt sätt att bygga en ungefär regelbunden tridecagon med regel och kompass. Källa: Wikimedia Commons.

Exempel på Tridecágel

Konkav och konvex åska

När de inre vinklarna i Tridecágono är mindre än 180 ° är figuren konvex, medan om en eller flera inre vinklar är större än 180º, så är Tridecágono konkav.

Den vanliga Tridecácácon är konvex, eftersom dess inre vinklar mäter cirka 152.3: e vardera.

Användning av Tridecágono i numismatik

Tjeckisk krona

Numismatics är vetenskapen om mynt, medaljer, biljetter och chips. Polygonerna på många sidor är idealiska som dekorativa element i utformningen av mynt, särskilt de som har många sidor, till exempel Tridecágono.

Inte alla mynt är runda, men polygonerna på många sidor liknar den cirkulära formen, desto fler sidor har det, desto större tillvägagångssätt. Därför använder myntdesigners polygonerna på många sidor för att introducera en touch av originalitet i sin design.

Olika polygoner används med detta ändamål, till exempel den övre valutan, kallad kronan och från Tjeckien, ett bra exempel på användningen av Tridecágono som designelement.

Referenser

1. Alexander, D. 2013. Geometri. Femte. Utgåva. Cengage Learning.
2. Teckning. Regelbundna polygoner. Återhämtad från: ritning.com.
3. Hartley, m. Konstruera en tridekagon. Återhämtat sig från: YouTube.com
4. Wikipedia. Byggbar polygon. Återhämtad från: är.Wikipedia.org.
5. Wikiwand. Tidekant. Återhämtat sig från: wikiwand.com.