Trianglar historia, element, klassificering, egenskaper

De trianglar De är platta och stängda geometriska figurer, som består av tre sidor. En triangel bestäms av tre linjer som skärs två till två och bildas med varandra tre vinklar. Den triangulära formen, full av symbolik, finns i otaliga föremål och som ett konstruktionselement.

Triangelns ursprung går förlorat i historien. Från arkeologiska bevis är det känt att primitiv mänsklighet kände honom väl, eftersom arkeologiska rester bekräftar att han användes i verktyg och vapen.

Figur 1. Trianglar. Källa: Public DomainPartures.

Det är också uppenbart att de forntida egyptierna hade solid kunskap om geometri och i synnerhet den triangulära formen. De förkroppsligades i de arkitektoniska elementen i deras monumentala konstruktioner.

I Rhind Papyrus finns formler för beräkning av trianglar och trapesområden, liksom vissa volymer och andra begrepp av rudimentär trigonometri.

Å andra sidan är det känt att babylonierna kunde beräkna området för triangeln och andra geometriska figurer, som de använde för praktiska ändamål, till exempel landets uppdelningar. De var också medvetna om många egenskaper hos trianglar.

Det var emellertid de antika grekerna som systematiserade många av de frekventa geometriska koncepten idag, även om mycket av den kunskapen inte var exklusiv, eftersom den verkligen delades med dessa andra forntida civilisationer.

[TOC]

Element i triangeln

Elementen i alla triangel anges i följande figur. Det finns tre: toppar, sidor och vinklar.

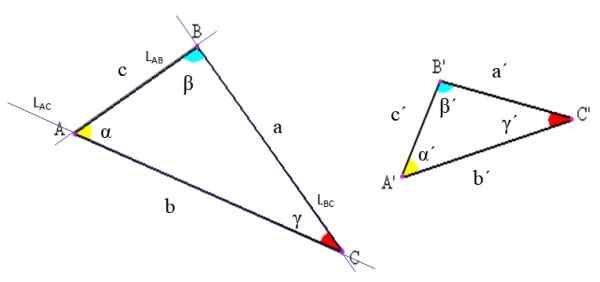figur 2. Notation av trianglar och deras element. Källa: Wikimedia Commons, modifierad av F. Zapata

-Häckar: Dessa är skärningspunkterna i linjerna vars segment avgör triangeln. I den övre figuren till exempel, linjen L_Växelström som innehåller AC -segmentet, korsar linjen L_Ab som innehåller segment AB precis vid punkt A.

-Sidor: Mellan varje par vertikaler ritas ett linjesegment som utgör en sida av triangeln. Detta segment kan betecknas med ändarna i ändarna eller använda ett specifikt brev för att kalla det. I exemplet i figur 2 kallas AB -sidan också "C".

-Vinklar: Mellan varje sida med ett gemensamt toppunkt har en vinkel sitt ursprung, vars toppunkt sammanfaller med triangeln. Vinkeln betecknas vanligtvis med en grekisk bokstav, som anges i början.

För att bygga en viss triangel, med en given form och storlek, har du bara några av följande datauppsättningar:

-De tre sidorna, ganska uppenbara i fallet med en triangel.

-Två sidor och vinkeln mellan dem, och den återstående sidan ritas omedelbart.

-Två vinklar (inre) och sidan mellan dem. I förlängningen dras de två saknade sidorna och triangeln är redo.

Notation

Generellt sett i notationen av trianglar används följande konventioner: vertikalerna anges med stora bokstäver, sidorna med små latinska bokstäver och vinklarna med grekiska bokstäver (se figur 2).

På detta sätt heter triangeln enligt dess vertikaler. Till exempel är triangeln till vänster i figur 2 ABC -triangeln, och den till höger är triangeln a'b'c '.

Det är också möjligt att använda andra notationer; Till exempel betecknas vinkel a i figur 2 som BAC. Observera att bokstaven i toppen går i mitten och bokstäverna är skrivna i motsatt riktning till klocknålarna.

Det kan tjäna dig: avgränsning av problemet

Andra gånger placeras en circumflex -accent för att beteckna vinkeln:

Eller symbolen ∠ används, eftersom föregående notation kanske inte är lätt i tryck, följt av bokstaven som motsvarar toppunkten:

α = ∠A

Typer av trianglar

Det finns flera trianglar klassificeringskriterier. Det vanligaste är att klassificera dem enligt måtten på deras sidor eller enligt måtten på deras vinklar. Beroende på måtten på deras sidor kan trianglarna vara: Scalenes, Isosceles eller Equidaterals:

-Skala: Dess tre sidor är olika.

-Likbent: Den har två olika sidor och en.

-Liksidig: De tre sidorna är desamma.

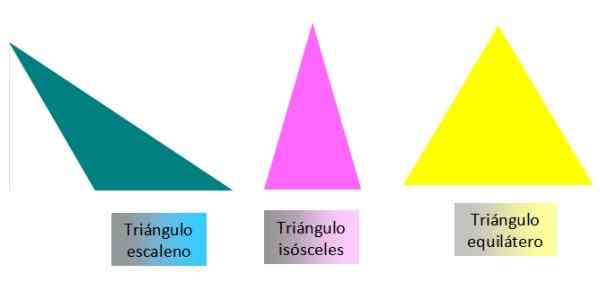Figur 3. Klassificering av trianglar på sina sidor. Källa: f. Zapata

Enligt måtten på deras vinklar kallas trianglarna så här:

-Trubbig, Om en av de inre vinklarna är större än 90º.

-Akut, När de tre inre vinklarna i triangeln är akuta, det vill säga mindre än 90º

-Rektangel, I händelse av att en av dess inre vinklar är värd 90º. Sidorna som bildar 90º kallas Catetos och motsatt sida till rätt vinkel är hypotenusen.

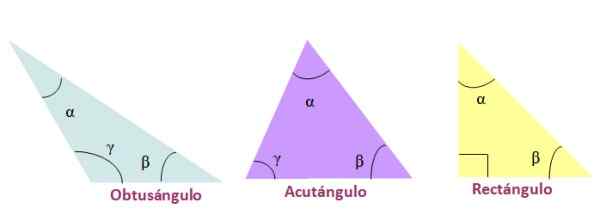Figur 4. Klassificering av trianglar av deras inre vinklar. Källa: f. Zapata.

Trianglar

När två trianglar har samma form och är av lika stor storlek sägs det att de är kongruenta. Naturligtvis är kongruensen relaterad till jämlikhet, så varför i geometri pratar vi om "två kongruenta trianglar" istället för "två lika trianglar"?

Tja, det är att föredra att använda termen "kongruens" för att hålla sig till sanningen, eftersom två trianglar kan ha samma form och storlek, men vara orienterad annorlunda i planet (se figur 3). Ur geometriens synvinkel skulle de inte längre vara samma.

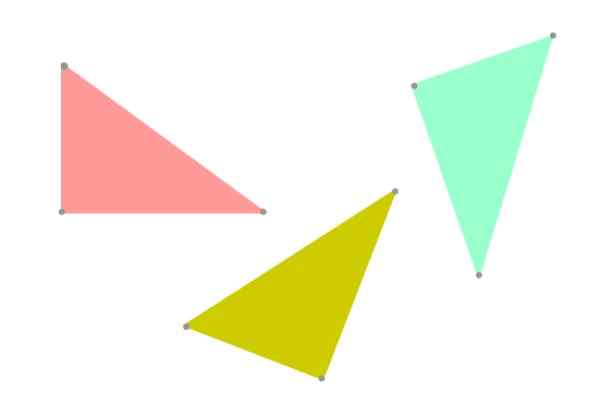Figur 5. Kongruenta trianglar, men inte nödvändigtvis samma, eftersom dess orientering i planet är annorlunda. Källa: f. Zapata.

Kongruenskriterier

Två trianglar är kongruenta om någon av följande situationer inträffar:

-De tre sidorna mäter samma (igen detta är det mest uppenbara).

-De har två identiska sidor och med samma vinkel mellan dem.

-Båda har två identiska inre vinklar och sidan mellan dessa vinklar är densamma.

Som man kan se handlar det om de två trianglarna uppfyller de nödvändiga förhållandena så att när de bygger dem är deras form och storlek exakt densamma.

Kongruenskriterierna är mycket användbara, eftersom i praktiken måste otaliga mekaniska delar och delar tillverkas i serie, så att deras åtgärder och form är exakt samma.

Trianglarnas likhet

En triangel liknar en annan om de har samma form, även om de har olika storlek. För att säkerställa att formen är densamma krävs att inre vinklar har samma värde och att sidorna är proportionella.

Figur 6. Två liknande trianglar: deras storlekar skiljer sig åt men deras proportioner är desamma. Källa: f. Zapata.

Trianglarna i figur 2 är också lika, liksom de i figur 6. Således:

Skarma A ', ∠ B = ∠ B 'och ∠ C = Ikt C '

När det gäller sidorna uppfylls följande skäl till likhet:

a/a '= b/b' = c/c '

Egenskaper

Trianglarnas grundläggande egenskaper är följande:

-Summan av de inre vinklarna i alla triangel är alltid 180º.

-För alla triangel är summan av dess yttre vinklar lika med 360 °.

Kan tjäna dig: grundläggande forskning: egenskaper, definition, exempel

- En yttre vinkel på en triangel är lika med summan av de två inre vinklarna som inte intill den vinkeln.

Teorier

Första satsen för sådant

De tillskrivs grekiska filosofer och matematiska berättelser om Miletus, som utvecklade flera teorier relaterade till geometri. Den första av dem upprättar följande:

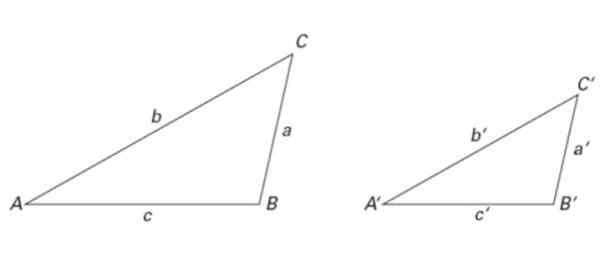
Om flera parallella linjer skär två tvärgående linjer, bestämmer de segment som är proportionella.

Figur 7. Tales Theorem. Källa: f. Zapata.

Med andra ord:

a/a '= b/b' = c/c '

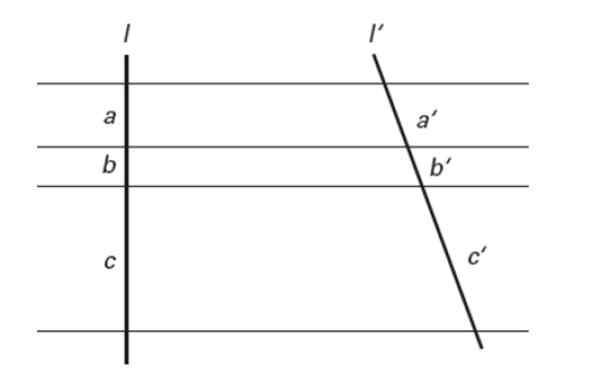
Det första teoremet för sådan är tillämplig på en triangel, till exempel finns ABC Blue Triangle till vänster, som skärs av de röda parallellerna till höger:

Figur 8. Satsen för sådana och liknande trianglar.

Violet Triangle of Violet liknar ABC Blue Triangle, därför kan följande enligt sådan teorem skrivas:

Ab '/ac' = ab/ac

Och det överensstämmer med vad som förklarades ovan i segmentet av trianglarna likhet. Förresten, parallella linjer kan också vara vertikala eller parallella med hypotenus och liknande trianglar erhålls.

Andra satsen för detta

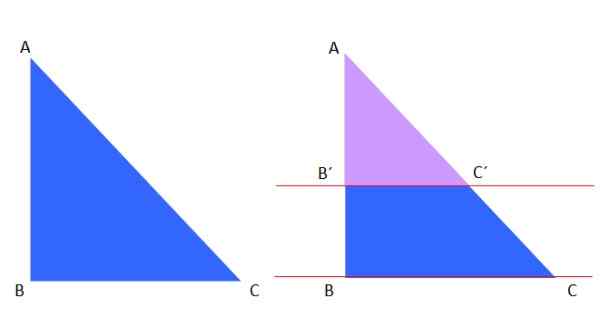
Detta sats hänvisar också till en triangel och en mittomkrets eller, som de som visas nedan. I denna figur är AC en diameter av omkretsen och B är en punkt för det, att vara B skiljer sig från A och B.

Den andra satsen för sådana stater att:

Vinkeln mellan AB- och BC -segmenten är alltid 90º, därför är ABC -triangeln rektangel.

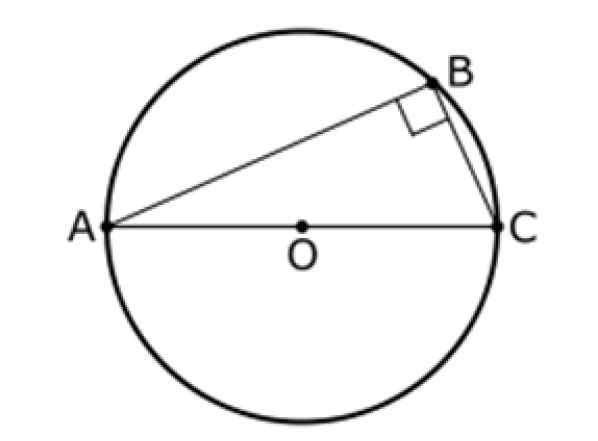Figur 9. Det andra teoremet för sådant. Källa: Wikimedia Commons. Induktiveload [public domain].

Pytagoras teorem

Detta är en av de mest kända teoremerna i historien. Det beror på den grekiska matematikern Pythagoras av Samos (569 - 475 till. C.) och är tillämplig på en höger triangel. Säger så:

Summan av rutorna i längderna Rektangeln triangelben är lika med längden på hypotenusen hög till torget.

Om vi ​​som ett exempel tar den blå triangeln i figur 8, eller den violetta triangeln, eftersom båda är rektanglar, kan det sägas att:

Växelström² = AB² + före Kristus² (Blå triangel)

Ac '² = Ab '² + FÖRE KRISTUS '² (Violet Triangle)

Området med en triangel

Triangelområdet ges av produkten från dess bas till och dess höjd h, dividerat med 2. Och genom trigonometri kan denna höjd skrivas som H = b sinθ.

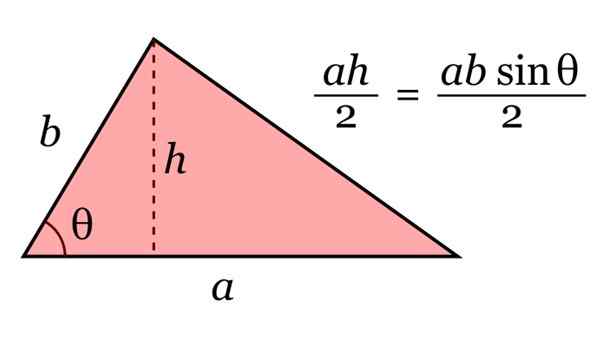Figur 10. Triangelområdet. Källa: Wikimedia Commons.

Exempel på trianglar

Exempel 1

Det sägs att genom sitt första teorem lyckades sådant mäta höjden på den stora pyramiden i Egypten, ett av de sju underverken i den antika världen och mäta skuggan som den projicerade på marken och den som projicerar en stav fast i marken.

Detta är proceduren för proceduren följt av sådant:

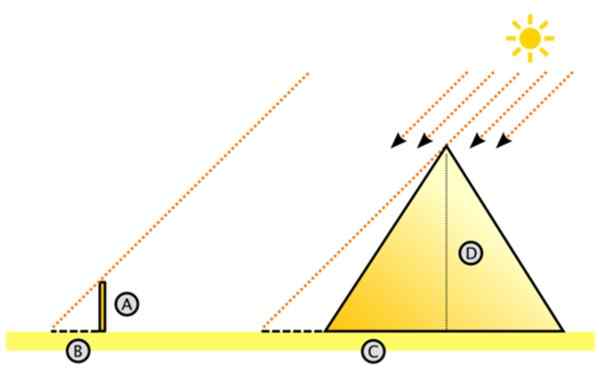Figur 11. Schema för att mäta höjden på den stora pyramiden genom likhet mellan trianglar. Källa: Wikimedia Commons. Dake [CC BY-SA 3.0 (http: // Creativecommons.Org/licenser/BY-SA/3.0/]]

Sådana med rätta antas att solens strålar påverkar parallellt. Med detta i åtanke föreställde han sig den stora högra triangeln.

Det finns höjden på pyramiden och C är avståndet på marken uppmätt från centrum till skuggan som projiceras av pyramiden på ökengolvet. Det kan vara mödosamt att mäta C, men det är verkligen lättare än att mäta höjden på pyramiden.

Till vänster är den lilla triangeln, från katter A och B, där A är höjden på staven som fastnar vertikalt på golvet och B är skuggan som den projicerar. Båda längderna är mätbara, precis som C (C är lika med skuggens längd + hälften av pyramidens längd).

Kan tjäna dig: vad är taktila stimuli?

Sedan, efter likhet mellan trianglar:

A/b = d/c

Och höjden på den stora pyramiden visar sig vara: D = C.(A/B)

Exempel 2

Civil konstruktion rustning är strukturer baserade på tunna ved eller metallstänger, som används som stöd i många byggnader. De är också kända som gitter, fack eller retikulerade (Trosseri på engelska).

I dem är trianglarna alltid närvarande, eftersom staplarna är sammankopplade vid punkter som kallas noder, som kan vara fixerade eller artikulerade.

Figur 12. Triangeln finns i ramen för denna bro. Källa: Pxhere.

Exempel 3

Metoden som kallas triangulering gör att du kan få platsen för otillgängliga punkter som känner till andra enklare avstånd att mäta, under förutsättning att en triangel bildas som inkluderar bland dess hörn den önskade platsen.

Till exempel i följande siffra vill du veta vid vilken punkt havet är fartyget, betecknat som B.

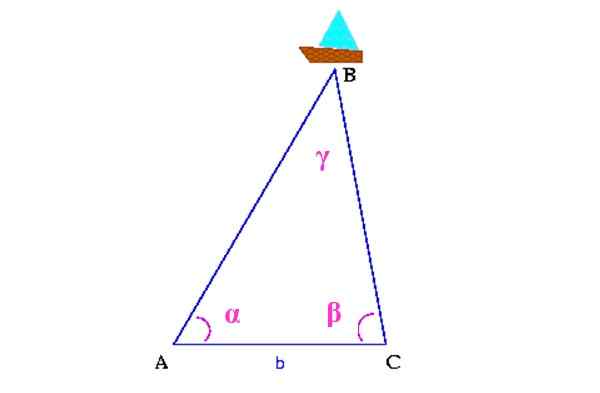Figur 13. Trianguleringssystem för att hitta fartyget. Källa: Wikimedia Commons. Colette [CC BY-SA 3.0 (http: // Creativecommons.Org/licenser/BY-SA/3.0/]]

Först mäts avståndet mellan två punkter på kusten, som i figuren är A och C. Då måste du bestämma vinklarna α och ß, med hjälp av en teodolit, En enhet som tjänar till att mäta vertikala och horisontella vinklar.

Med all denna information byggs en triangel på vars övre topp är fartyget. Det skulle minska vinkeln y, med hjälp av medel.

Övningar

Övning 1

I den visade figuren är solens strålar parallella. På detta sätt projicerar den 5 -meter höga trädet en 6 -meter skugga på marken. Samtidigt är byggnadens skugga 40 meter. Efter ett sådant teorem av sådant, hitta byggnadens höjd.

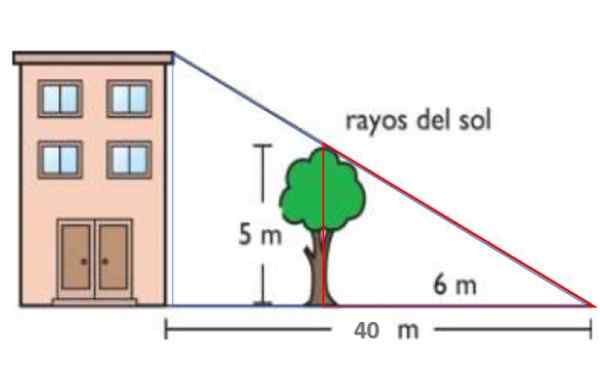Figur 14. Årets schema löst 1. Källa: f. Zapata.

Lösning

Den röda triangeln har sidor på 5 respektive 6 meter, medan den blå har en höjd h -höjden på byggnaden och basen 40 meter. Båda trianglarna liknar därför:

H / 40 = 5/6 → H = 40.(5/6) m = 33.3 m

Övning 2

Du måste veta det horisontella avståndet mellan två punkter TILL och B, Men de är belägna på en mycket oregelbunden terräng.

Ungefär vid mittpunkten (s_m) Från detta land sticker en framträdande på 1.75 meter högt. Om bandmåttet indikerar 26 meter i längd uppmätt från A till framträdande och 27 meter från B till samma punkt, hitta avståndet Ab.

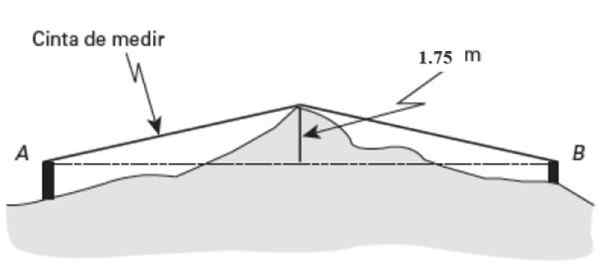Figur 15. Schema för övningen löste 2. Källa: Jiménez, R. Matematik II. Geometri och trigonometri.

Lösning

Pythagoras Theorem tillämpas på en av de två rektanglarnas trianglar i figuren. Börjar med den till vänster:

Hypotenus = c = 26 meter

Höjd = a = 1.75 meter

Ap_m = (26² - 1.75²)^1/2 = 25.94 m

Nu appliceras Pythagoras i den högra triangeln, denna gång C = 27 meter, a = 1.75 meter. Med dessa värden:

Bp_m= (27² - 1.75²)^1/2 = 26.94 m

Avståndet AB lägger till dessa resultat:

Ab = 25.94 m +26.94 m = 52.88 m.

Referenser

1. Baldor, J. TILL. 1973.Platt och rymdgeometri. Centralamerikansk kultur.
2. BARREDO, D. Triangelns geometri. Återhämtat sig från: ficus.pntisk.Mec.är.
3. Jiménez, r. 2010. Matematik II. Geometri och trigonometri. Andra upplagan. Pearson.
4. Wentworth, g. Planetgeometri. Återhämtat sig från: Gutenberg.org.
5. Wikipedia. Triangel. Återhämtad från: är. Wikipedia.org.