Egenskaper sneda trianglar, exempel, övningar

De Sneda trianglar De är de som inte har någon rätt vinkel, därför är ingen av deras inre vinklar lika med 90º. Så en sned triangel kan vara Akut eller trubbig.

I det första fallet är de inre vinklarna i triangeln akuta eller vad som är densamma: mindre än 90º, medan det i den andra alltid finns en vinkel större än 90º, det vill säga en stöt vinkel. Låt oss titta på ett exempel på var och en i följande figur:

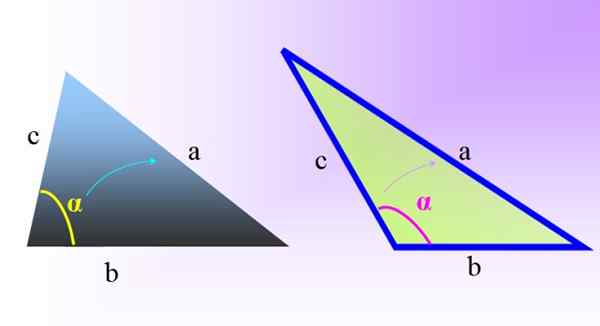Figur 1. Sneda trianglar: till vänster en sned och akutangel triangel. Till höger en sned och stöt triangel. Källa: f. Zapata.

För att hitta sidorna på sidorna och måtten på de inre vinklarna på denna typ av trianglar, i frånvaro av raka vinklar är det inte möjligt att applicera Pythagoras teorem.

Det finns emellertid alternativ för att lösa triangeln: kosinusens teorier och bröstet och det faktum att summan av de inre vinklarna är lika med 180º.

[TOC]

Oblicuágulos trianglar exempel

Vägled oss ​​i figur 1 kan vi lätt känna igen de sneda trianglarna genom två kriterier som vi kommer att ge nedan.

Acutangle triangel

Vara triangeln på sidorna A, B och C, med α vinkeln framför sidan till.

Om torget på sidan mittemot den akuta vinkeln α är mindre än summan av kvadrarna på de återstående sidorna, är triangeln akutangel. Algebraiskt:

till² < b² + c²; a < 90º

Den relativa liksidiga triangeln, den som har sina tre sidor av samma mått, är akutangel och därför sned, eftersom dess inre vinklar är lika och mäter 60º.

Triangel

Å andra sidan, om torget på motsatt sida till Vid stötvinkeln är det större än summan av de andra två summan, vi är i närvaro av en stöt triangel. Därför:

till² B² + c²; α> 90º

Till exempel är en triangel vars inre vinklar är 105º, 60º och 15º en stöt sned triangel. Observera att 105º + 60º + 15º = 180º.

Sinus och kosinus teorier

För att lösa de sneda trianglarna, det vill säga för att hitta måtten på alla deras sidor och alla deras vinklar, krävs teorems av bröstet och kosinus.

Låt A, B och C sidorna på en triangel och α, ß och y deras inre vinklar. Så:

Bröstteorem

Bröstteoremet upprättar följande:

Där a är motsatt vinkel mot sida A är ß vinkeln i motsats till sidan B och y är vinkeln framför sidan C.

Det kan tjäna dig: antiderivativ: formler och ekvationer, exempel, övningar

Likvärdig:

Vi väljer att tillämpa bröstteoremet när vi ska lösa en triangel än fler vinklar är kända än sidor.

Coseno Theorem

Enligt Coseno Theorem:

c² = a² + b² - 2⋅A⋅B⋅COS y

Återigen är vinkeln γ framför sidan C. Vi kan också skriva motsvarande uttryck för sidor A och B, enligt följande:

till² = B² + c² - 2⋅B⋅C⋅COS a

OCH

b² = a² + c² - 2⋅A⋅C⋅COS β

Cosine Theorem tillämpas helst när värdet på två sidor och vinkeln mellan dem är känd. När de tre sidorna av en triangel har varit känd tillåter teoremet oss att beräkna kosinusen i vinkeln mellan två av dem.

Löst övningar

- Övning 1

Kontrollera att triangeln vars sidor mäter 20, 10 och 12 godtyckliga enheter är stöt.

Lösning

Vi känner inte till någon av de inre vinklarna, men enligt kriterierna som tjänar till att erkänna stötta trianglar kan vi höja ojämlikheter med sidorna på sidorna för att observera om det är uppfyllt.

Först hittar vi rutorna på varje sida:

tjugo² = 400

10² = 100

12² = 144

Och vi ser att det verkligen: 400> 100 + 144, sedan 400> 244. Därför innehåller triangeln en vinkel större än 90º, belägen framför sidan som mäter 20. Följaktligen är denna triangel, förutom att vara sned, också stöt.

- Övning 2

Med tanke på den sneda triangeln som visas i figur 2, vars åtgärder ges i godtyckliga enheter, bestäm: Bestäm:

a) Värdet på x. Är det en akutangel eller en stöt triangel?

b) de återstående inre vinklarna i triangeln

c) omkrets

d) område.

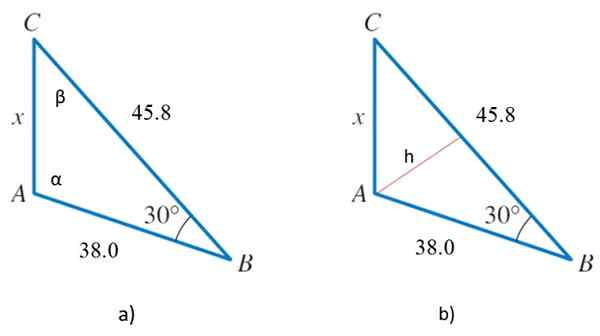figur 2. 2a) Triangel för året löst 2 och 2b) samma triangel med en höjd, som kommer att tjäna till att bestämma området. Källa: f. Zapata.

Lösning till

Av triangeln är två angränsande sidor kända, vars åtgärder är 38.0 och 45.8 och vinkeln mellan dem, som är 30º, därför appliceras kosinussteoremet omedelbart:

x² = 38.0² + Fyra fem.8² - 2 x 38.0 x 45.8 x cos 30º = 527.18

Därför:

x = (527.18)^1/2 = 22.96

Ritningen antyder att a> 90º och triangeln är stöt, förutom sned. För att kontrollera det hittar vi sidorna på sidorna, som gjordes i föregående övning:

22.96² = 527.18

38.0² = 1444.00

Fyra fem.8² = 2097.64

Vinkeln a är större än 90º om den är sant än kvadratet på motsatt sida: 45.8²  Det är större än summan av kvadrarna på de andra sidorna, vilket är 22.96² + 38.0².

Kan tjäna dig: exponenters lagar

Låt oss se om det händer:

527.18 + 1444.00 = 1971.2

Verkligen:

2097.64> 1971.2

Därför är vinkeln a större än 90º.

Lösning B

Nu kan vi tillämpa bröstteoremet för att hitta en av de saknade vinklarna. Vi kommer att höja den för vinkel β:

Sen 30º / 22.96 = sin β / 38

Sen β = 38 x (SEN 30º / 22.96) = 0.8275

β = bågen (0.8275) = 55.84º

Den saknade vinkeln kan hittas med att veta att summan av de inre vinklarna i alla triangeln är 180º. Därför:

55.84º + 30º + α = 180º

α = 94.16º

Om du föredrar kan du också använda kosinussteoremet för att hitta kosinusen i vinkeln som är mellan två angränsande sidor. När Coseno Arc -funktionen används för att bestämma vinkeln.

Resultaten kan skilja sig lite i decimalerna, enligt avrundningen.

Lösning C

Omkretsen P är figurens kontur, motsvarande summan av måtten på de tre sidorna:

P = 22.96 + 38.00 + 45.80 = 106.76 godtyckliga enheter.

Lösning D

Formeln för att beräkna området för alla triangel är:

A = (1/2) x bas x höjd

Vi måste välja en av sidorna som bas och bestämma höjden. Till exempel att välja sidan som mäter 45.8, vi ritar höjden h Tills Vertex A, som är den röda linjen i figur 2B.

Genom att göra detta delar vi upp den ursprungliga triangeln i två rektanglar, båda med h Som en vanlig kateto. Någon av dem tjänar, eftersom vi känner till en skarp sida och vinkel.

Vi kommer att ta den som har hypotenusa lika med 38, en kategori som mäter h, vilket är den sökta höjden och den akuta vinkeln lika med 30º.

Med hjälp av de trigonometriska orsakerna till den akuta vinkeln 30º bestämmer vi värdet på h:

Sen 30º = Cateto mittemot 30º / Hypotenusa = H / 38

H = 38 x sen 30º = 19

Därför:

A = (1/2) x 45.8 x 19 = 435.1 godtyckliga områden i området.

Vi kunde ha valt en annan sida som bas, till exempel sida 38, i så fall höjden h Det är annorlunda, eftersom en annan rektangel triangel bildas, men resultatet av området är detsamma. Det återstår som träning för läsaren att kontrollera det.

- Övning 3

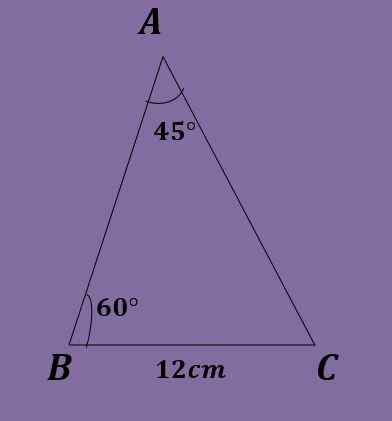
Med tanke på en ABC -triangel som A = 45º, B = 60º och A = 12 cm, beräkna de andra triangeldata.

Kan tjäna dig: tecken på gruppering

Lösning

Med hjälp av att summan av de inre vinklarna i en triangel är lika med 180º den måste:

C = 180º-45º-60º = 75º.

De tre vinklarna är redan kända. Sedan fortsätter vi att använda bröstlagen för att beräkna de två sidorna som saknas.

Ekvationerna som uppstår är 12 / utan (45º) = B / utan (60º) = C / utan (75º).

Från den första jämlikheten kan du rensa "B" och få det:

B = 12*utan (60º)/utan (45º) = 6√6 ≈ 14.696 cm.

Du kan också rensa "C" och få det:

C = 12*sin (75º)/sin (45º) = 6 (1+√3) ≈ 16.392 cm.

- Övning 4

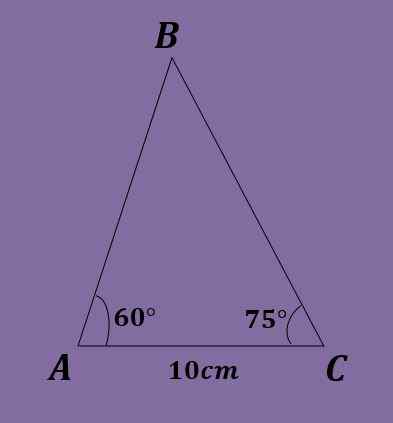
Med tanke på triangeln ABC så att A = 60º, C = 75º och B = 10 cm, beräkna de andra triangeldata.

Lösning

Som föregående år måste du b = 180º-60º-75º = 45º. Dessutom använder du bröstlagen till / utan (60º) = 10 / utan (45º) = C / utan (75º), där det erhålls att a = 10*utan (60º) / utan (45º) = 5 √6 ≈ 12.247 cm och c = 10*sin (75º)/utan (45 °) = 5 (1+√3) ≈ 13.660 cm.

- Övning 5

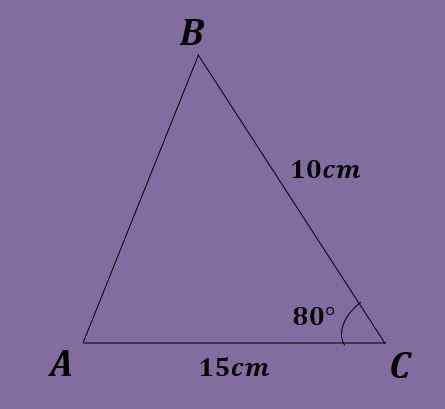
Med tanke på triangeln ABC så att a = 10 cm, b = 15 cm och c = 80º, beräkna de andra triangeldata.

Lösning

I denna övning är bara en vinkel känd, därför är det inte möjligt att börja som det gjordes i de två tidigare övningarna. Dessutom kan bröstlag inte tillämpas eftersom ingen ekvation kunde lösas.

Därför tillämpas lagen om Cosenos. Du måste:

C² = 10²+15² - 2 (10) (15) cos (80º) = 325 - 300*0.173 ≈ 272.905 cm,

Så att c ≈ 16.51 cm. Nu, att känna till de tre sidorna, används bröstlagen och det erhålls att:

10 / utan (a) = 15 / utan (b) = 16.51 cm /utan (80º).

Härifrån, när Clear B är utan (B) = 15*utan (80º)/ 16.51 ≈ 0.894, vilket innebär att B ≈ 63.38º.

Nu kan det erhållas att a = 180º - 80º - 63.38º ≈ 36.62º.

- Övning 6

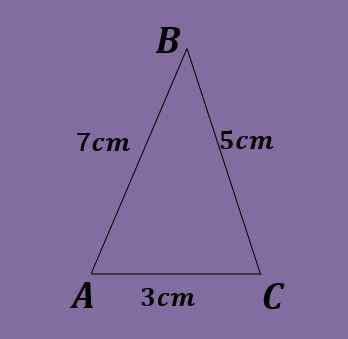
Sidorna på en sned triangel är a = 5 cm, b = 3 cm och c = 7 cm. Beräkna triangelns vinklar.

Lösning

Återigen kan bröstlagen inte tillämpas direkt, eftersom ingen ekvation skulle tjäna till att få vinklens värde.

Med hjälp av kosinuslagen måste du till C² = A² + B² - 2AB COS (C), varifrån när Cos (C) = (A² + B² - C²)/ 2AB = (5² + 3² -7²)/ 2*5 *3 = -15/30 = -1/2 och därför c = 120º.

Nu kan bröstlagen tillämpas och därmed erhålla 5/utan (a) = 3/utan (b) = 7/utan (120º), där b kan rensas b och erhålla det utan (b) = 3* utan (120º )/7 = 0.371, så att b = 21.79º.

Slutligen beräknas den sista vinkeln med hjälp av att A = 180º-1330º-21.79º = 38.21: e.

Referenser

1. Clemens, s. Geometri med applikationer. Addison Wesley.
2. Ibáñez, s. 2010. Matematik III. Cengage Learning.
3. Jiménez, r. Matematik II: Geometri och trigonometri. 2: a. Utgåva. Pearson.
4. Matematik för dig. Triangel. Återhämtat sig från: matematik för.WordPress.com.
5. Stewart, J. 2007. Förkalkning. Femte. Utgåva. Cengage Learning.